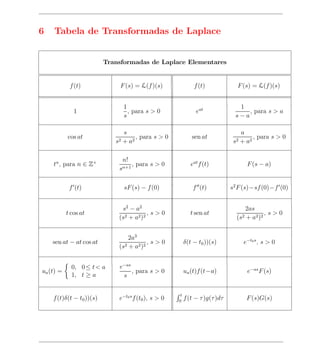
1. A transformada de Laplace é usada para resolver equações diferenciais lineares com coeficientes constantes, transformando a equação diferencial inicial em uma equação algébrica. 2. A transformada de Laplace de uma função f(t) é definida como a integral de f(t) multiplicada por e^-st de 0 a infinito. Isso mapeia funções do domínio temporal para o domínio complexo. 3. Exemplos mostram como calcular a transformada de Laplace de funções comuns como exponenciais, seno, cosseno, polinomiais e combinações

1. 1 Introdu¸˜o
ca
A transformada de Laplace pode ser usada para resolver equa¸oes diferencias lineares com
c˜
coeficientes constantes, ou seja, equa¸oes da forma
c˜
ay + by + cy = f (t), para a, b, c ∈ R
Para isso, a equa¸ao diferencial ´ inicialmente transformada pela transformada de Laplace
c˜ e
numa equa¸ao alg´brica. Depois resolve-se a equa¸ao alg´brica e finalmente transforma-se
c˜ e c˜ e
de volta a solu¸ao da equa¸ao alg´brica na solu¸ao da equa¸ao diferencial inicial.
c˜ c˜ e c˜ c˜
A transformada de Laplace de uma fun¸ao f : [0, ∞) → R ´ definida por
c˜ e
∞
L(f )(s) = F (s) = e−st f (t)dt.
0
para todo s ≥ 0 em que a integral acima converge. Representaremos a fun¸ao original por
c˜
uma letra min´scula e a sua vari´vel por t, e a sua transformada de Laplace pela letra
u a
correspondente mai´scula e a sua vari´vel. Por exemplo, as transformadas de Laplace das
u a
fun¸oes f (t), g(t) e h(t) ser˜o representadas por F (s), G(s) e H(s), respectivamente.
c˜ a
Exemplo 1. A transformada de Laplace da fun¸ao f : [0, ∞) → R definida por f (t) = 1
c˜
´ dada por
e
∞ ∞
e−st e−sT e−s0 e−s0 1
F (s) = e−st 1 dt = = lim − =0− = , para s > 0.
0 −s 0
T →∞ −s −s −s s
Exemplo 2. Seja a uma constante real. A transformada de Laplace da fun¸ao
c˜
f : [0, ∞) → R definida por f (t) = eat ´ dada por
e
∞ ∞ ∞
−st at −(s−a)t e−(s−a)t e−(s−a)0 1
F (s) = e e dt = e dt = = 0− = , para s > a.
0 0 a−s 0 a−s s−a

2. Exemplo 3. Seja a uma constante real. Vamos determinar a transformada de Laplace
das fun¸oes f : [0, ∞) → R dada por f (t) = cos at e g : [0, ∞) → R dada por g(t) = sen at.
c˜
Para isso, vamos calcular a transformada de Laplace da fun¸ao
c˜
h : [0, ∞) → R definida por h(t) = eiat .
∞ ∞ ∞
−st iat −(s−ia)t e−(s−ia)t
H(s) = e e dt = e dt =
0 0 −(s − ia) 0
e−(s−ia)0 e−(s−ia)0
= lim e−sT (cos aT + i sen aT ) − =0−
T →∞ −(s − ia) ia − s
1
= , para s > 0.
s − ia
Calculamos a acima a transformada de Laplace de
h(t) = eiat = cos at + i sen at = f (t) + ig(t)
∞
H(s) = L(h)(s) = e−st (cos at + i sen at) dt = L(f )(s) + iL(g)(s) = F (s) + iG(s)
0
Comparando a parte real (imagin´ria) do lado direito com a parte real (imagin´ria) do
a a
lado esquerdo da igualdade obtemos
1 s + ia s
F (s) = Re{ } = Re{ }= 2 , para s > 0
s − ia (s − ia)(s + ia) s + a2
1 s + ia a
G(s) = Im{ } = Im{ }= 2 , para s > 0.
s − ia (s − ia)(s + ia) s + a2
Exemplo 4. Seja n um inteiro positivo. Vamos calcular a transformada de Laplace da
fun¸ao f : [0, ∞) → R dada por fn (t) = tn , para n = 0, 1, 2, . . .
c˜
∞
∞
tn est n ∞
Fn (s) = e t dt = −st n
− e−st tn−1 dt
0 −s 0 −s 0
∞
n n
= e−st tn−1 dt = Fn−1 (s)
s 0 s
Aplicando-se recursivamente a f´rmula obtida obtemos
o
n(n − 1) n(n − 1) . . . 1
Fn (s) = Fn−2 (s) = F0 (s)
s2 sn

3. 1
mas F0 (s) = ´ a transformada de Laplace da fun¸ao constante 1, ou seja, F0 (s) = 1 .
e c˜ s
s n
Assim, a transformada de Laplace de fn (t) = t , para n = 0, 1, 2, . . . ´
e
n!
Fn (s) = , para s > 0.
sn+1
Para calcular a transformada de Laplace de outras fun¸oes vamos usar as propriedades
c˜
que apresentamos a seguir.
Teorema 1 (Linearidade). Se a transformada de Laplace de f (t) ´ F (s), para s > a 1 ,
e
e a transformada de Laplace de g(t) ´ G(s), para s > a2 , ent˜o para constantes α e β
e a
L(αf + βg)(s) = αL(f )(s) + βL(g)(s) = αF (s) + βG(s), para s > max{a 1 , a2 }.
Teorema 2 (1o Teorema de Deslocamento). Seja a uma constante. Se a transfor-
.
mada de Laplace da fun¸ao f : [0, ∞) → R ´ F (s), para s > c, ent˜o a transformada de
c˜ e a
Laplace da fun¸ao
c˜
g(t) = eat f (t)
´
e
G(s) = F (s − a), para s > a + c
Exemplo 5. Sejam a e b constantes. Usando o Teorema anterior obtemos que a trans-
formada de Laplace de f : [0, ∞) → R dada por f (t) = ebt cos at ´ dada por
e
s−b
F (s) = , para s > a.
(s − b)2 + a2

4. Exemplo 6. Sejam a e b constantes. Usando o Teorema anterior obtemos que a trans-
formada de Laplace de f : [0, ∞) → R dada por f (t) = ebt sen at ´ dada por
e
a
F (s) = , para s > a.
(s − b)2 + a2
Exemplo 7. Seja a um constante e n um inteiro positivo. Usando o Teorema anterior
obtemos que a transformada de Laplace de f : [0, ∞) → R dada por f (t) = eat tn ´ dada
e
por
n!
F (s) = , para s > a.
(s − a)n+1
Exemplo 8. Seja a uma constante. Pelo Teorema anterior a transformada de Laplace
eat + e−at
do cosseno hiperb´lico de at, f (t) = cosh at =
o , ´ dada por
e
2
1 1 1 1 s
F (s) = + = 2 , para s > |a|.
2s−a 2s+a s − a2
Exemplo 9. Seja a uma constante. Pelo Teorema anterior a transformada de Laplace
eat − e−at
do seno hiperb´lico de at, f (t) = senh at =
o , ´ dada por
e
2
1 1 1 1 a
F (s) = − = 2 , para s > |a|.
2s−a 2s+a s − a2
Exemplo 10. Se a transformada de Laplace de uma fun¸ao f (t) ´
c˜ e
s+3
F (s) =
s2 − 3s + 2
ent˜o vamos determinar a fun¸ao f (t). Para isso vamos decompor F (s) em fra¸oes parci-
a c˜ c˜
ais. O denominador de F (s) tem duas ra´ reais s = 1 e s = 2. Assim,
ızes
s+3 A B
F (s) = = + ,
(s − 1)(s − 2) s−1 s−2
em que A e B s˜o constantes a determinar. Multiplicando F (s) por (s − 1)(s − 2) obtemos
a
s + 3 = A(s − 2) + B(s − 1) = (A + B)s + (−2A − B)

5. Comparando os termos de mesmo grau obtemos
1=A+B e 3 = −2A − B
de onde obtemos que A = −4 e B = 5. Assim,
s+3 1 1
F (s) = = −4 +5
(s − 1)(s − 2) s−1 s−2
e a fun¸ao cuja transformada ´ F (s) ´
c˜ e e
f (t) = −4et + 5e2t .
Exemplo 11. Se a transformada de Laplace de uma fun¸ao f (t) ´
c˜ e
s−3
F (s) = 2
s + 4s + 4
ent˜o vamos determinar a fun¸ao f (t). O denominador de F (s) tem somente uma raiz
a c˜
real, s = 2. Podemos reescrever F (s) da seguinte forma
s−3 s+2−5 s+2 −5 1 1
F (s) = = = + = −5 .
(s + 2) 2 (s + 2) 2 (s + 2) 2 (s + 2) 2 s+2 (s + 2)2
Observando a Tabela na p´gina 20, usando o 1o Teorema do deslocamento e o Teorema
a .
da Linearidade vemos que a fun¸ao cuja transformada de Laplace ´ F (s) ´ dada por
c˜ e e
f (t) = e−2t − 5e−2t t.
Exemplo 12. Se a transformada de Laplace de uma fun¸ao f (t) ´
c˜ e
s−2
F (s) = 2
2s + 2s + 2
ent˜o vamos determinar a fun¸ao f (t). Completando quadrados podemos reescrever F (s)
a c˜
da seguinte forma
s−2 s−2 s−2
F (s) = = =
2s2
+ 2s + 2 2[s 2 + s + 1] 2[(s + 1/2)2 + 3/4]
s + 1/2 − 5/2 s + 1/2 5/2
= 2 + 3/4]
= 2 + 3/4]
−
2[(s + 1/2) 2[(s + 1/2) 2[(s + 1/2)2 + 3/4]
1 s + 1/2 5 1
= 2 + 3/4
−
2 (s + 1/2) 4 (s + 1/2)2 + 3/4
√
1 s + 1/2 5 3/2
= 2 + 3/4
− √
2 (s + 1/2) 2 3 (s + 1/2)2 + 3/4

6. Observando a Tabela na p´gina 20, usando o 1o Teorema do deslocamento e o Teorema
a .
da Linearidade vemos que a fun¸ao cuja transformada de Laplace ´ F (s) ´ dada por
c˜ e e
√ √
1 3 5 3
f (t) = e−t/2 cos t − √ e−t/2 sen t .
2 2 2 3 2

7. 2 Solu¸˜o de Problemas de Valor Inicial
ca
Dizemos que uma fun¸ao f : [0, ∞) → R ´ seccionalmente cont´
c˜ e ınua ou cont´
ınua
por partes se f (t) ´ cont´
e ınua em [0, ∞) exceto possivelmente em um n´mero finito de
u
pontos, nos quais os limites laterais existem.
Teorema 3 (Deriva¸˜o).
ca (a) Suponha que f : [0, ∞) → R seja deriv´vel com f (t)
a
seccionalmente cont´
ınua. Ent˜o
a
L(f )(s) = sF (s) − f (0),
em que F (s) ´ a transformada de Laplace de f (t).
e
(b) Suponha que f : [0, ∞) → R seja deriv´vel duas vezes com f (t) seccionalmente
a
cont´
ınua. Ent˜o
a
L(f )(s) = s2 F (s) − sf (0) − f (0),
em que F (s) ´ a transformada de Laplace de f (t).
e
Exemplo 13. Seja a uma constante. Seja f (t) = t sen at. Vamos determinar F (s).
f (t) = sen at + at cos at
f (t) = 2a cos at − a2 t senat = 2a cos at − a2 f (t)
Assim, aplicando-se a transformada de Laplace e usando o Teorema anterior obtemos
s
s2 F (s) − sf (0) − f (0) = 2a − a2 F (s)
s2 + a2
Assim,
2as
F (s) =
(s2 + a2 )2

8. Exemplo 14. Seja a uma constante. Seja f (t) = t cos at. Deixamos como exerc´
ıcio
mostrar que
s2 − a 2
F (s) = 2
(s + a2 )2
Exemplo 15. Vamos resolver o seguinte problema de valor inicial
y + 2y + 5y = 4e−t cos 2t, y(0) = 1, y (0) = 0
Aplicando-se a transformada de Laplace a equa¸ao acima obtemos
` c˜
s+1
s2 Y (s) − sy(0) − y (0) + 2 (sY (s) − y(0)) + 5Y (s) = 4
(s + 1)2 + 4
Substituindo-se os valores y(0) = 1 e y (0) = 0 obtemos
s+1
s2 + 2s + 5 Y (s) = 4 +s+2
(s + 1)2 + 4
4s + 4 + (s + 2)(s2 + 2s + 5)
=
s2 + 2s + 5
s3 + 4s2 + 13s + 14
=
s2 + 2s + 5
Assim,
s3 + 4s2 + 13s + 14
Y (s) =
(s2 + 2s + 5)2
Como o denominador tem somente ra´
ızes complexas, para decompor Y (s) em fra¸oes
c˜
parciais vamos encontrar A, B, C e D tais que
As + B Cs + D
Y (s) = + 2
+ 2s + 5 (s + 2s + 5)2
s2
ou seja
s3 + 4s2 + 13s + 14 = (As + B)(s2 + 2s + 5) + (Cs + D)
= As3 + (B + 2A)s2 + (2B + 5A + C)s + (5B + D)

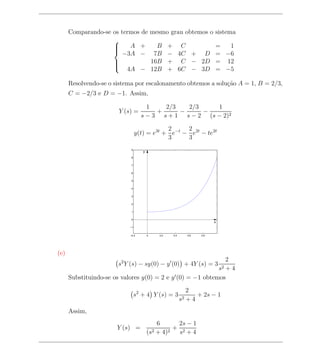
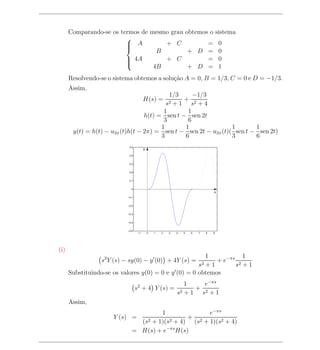
9. Comparando-se os termos de mesmo grau obtemos o sistema

 A
 = 1
2A + B = 4

 5A + 2B + C
 = 13
5B + D = 14

que tem solu¸ao A = 1, B = 2, C = 4 e D = 4. Assim,
c˜
s+2 4s + 4 s+1+1 s+1
Y (s) = + 2 = +4
s2 + 2s + 5 (s + 2s + 5)2 (s + 1)2 + 4 [(s + 1)2 + 4]2
s+1 1 2 2 · 2(s + 1)
= + +
(s + 1)2 + 4 2 (s + 1)2 + 4 [(s + 1)2 + 4]2
De onde obtemos
1
y(t) = e−t cos 2t + e−t sen 2t + te−t sen 2t
2

10. 6 Tabela de Transformadas de Laplace
Transformadas de Laplace Elementares
f (t) F (s) = L(f )(s) f (t) F (s) = L(f )(s)
1 1
1 , para s > 0 eat , para s > a
s s−a
s a
cos at , para s > 0 sen at , para s > 0
s2 + a2 s2 + a2
n!
tn , para n ∈ Z+ , para s > 0 eat f (t) F (s − a)
sn+1
f (t) sF (s) − f (0) f (t) s2 F (s)−sf (0)−f (0)
s2 − a 2 2as
t cos at ,s>0 t sen at ,s>0
(s2 + a2 )2 (s2 + a2 )2
2a3
sen at − at cos at ,s>0 δ(t − t0 ))(s) e−t0 s , s > 0
(s2 + a2 )2
0, 0 ≤ t < a e−as
ua (t) = , para s > 0 ua (t)f (t−a) e−as F (s)
1, t ≥ a s
t
f (t)δ(t − t0 ))(s) e−t0 s f (t0 ), s > 0 0
f (t − τ )g(τ )dτ F (s)G(s)

11. 7 Exerc´
ıcios
1. Resolva os problemas de valor inicial:
(a) y + y − 2y = 2t, y(0) = 0, y (0) = 1
(b) y + 4y = t2 + 3et , y(0) = 0, y (0) = 2
(c) y − 2y + y = tet + 4, y(0) = 1, y (0) = 1
(d) y − 2y − 3y = 3te2t , y(0) = 1, y (0) = 0
(e) y + 4y = 3 sen 2t, y(0) = 2, y (0) = −1
1, para 0 ≤ t < π/2
(f) y + y = f (t), y(0) = 0,y (0) = 1, em que f (t) =
0, para t ≥ π/2

 0, para 0 ≤ t < π
(g) y +2y +2y = f (t), y(0) = 0,y (0) = 1, em que f (t) = 2, para π ≤ t < 2π
0, para t ≥ 2π

sen t, para 0 ≤ t < 2π
(h) y + 4y = f (t), y(0) = 0,y (0) = 0, em que f (t) =
0, para t ≥ 2π
sen t, para 0 ≤ t < π
(i) y + 4y = f (t), y(0) = 0,y (0) = 0, em que f (t) =
0, para t ≥ π
1, para 0 ≤ t < 10
(j) y + 3y + 2y = f (t), y(0) = 0,y (0) = 0, em que f (t) =
0, para t ≥ 10
0, para 0 ≤ t < 2
(k) y + 3y + 2y = f (t), y(0) = 0,y (0) = 1, em que f (t) =
1, para t ≥ 2
0, para 0 ≤ t < 3π
(l) y + y = f (t), y(0) = 0,y (0) = 1, em que f (t) =
1, para t ≥ 3π
5 sen t, para 0 ≤ t < π
(m) y +y + 4 y = f (t), y(0) = 0,y (0) = 0, em que f (t) =
0, para t ≥ π

 0, para 0 ≤ t < π
(n) y + 4y = f (t), y(0) = 0,y (0) = 0, em que f (t) = 2, para π ≤ t < 3π
0, para t ≥ 3π

(o) y + y = δ(t − 2π) cos t, y(0) = 0, y (0) = 1
(p) y + 4y + 4y = f (t), y(0) = 2, y (0) = −3
2. Resolva o problema: y − 6y + 8y = sen t, y(0) = y (0) = 0

12. (a) sem usar transformada de Laplace
(b) usando transformada de Laplace

13. 8 Respostas dos Exerc´
ıcios
1. (a)
1
s2 Y (s) − sy(0) − y (0) + (sY (s) − y(0)) − 2Y (s) = 2
s2
Substituindo-se os valores y(0) = 0 e y (0) = 1 obtemos
2
s2 + s − 2 Y (s) = +1
s2
Assim,
2 1
Y (s) = +
s2 (s
+ 2)(s − 1) (s + 2)(s − 1)
2 + s2
= 2
s (s + 2)(s − 1)
A B C D
Y (s) = + 2+ +
s s s+2 s−1
s2 + 2 = As(s2 + s − 2) + B(s2 + s − 2) + Cs2 (s − 1) + Ds2 (s + 2)
= (A + C + D)s3 + (A + B − C + 2D)s2 + (−2A + B)s + (−2B)
Comparando-se os termos de mesmo grau obtemos o sistema


 A + C + D = 0
A + B − C + 2D = 1

 −2A + B
 = 0
− 2B = 2

que tem solu¸ao A = −1/2, B = −1, C = −1/2 e D = 1. Assim,
c˜
−1/2 1 1/2 1
Y (s) = − 2− +
s s s+2 s−1
1 1
y(t) = − − t − e−2t + et
2 2

14. 5
y
4
3
2
1
0
x
−1
0 0.5 1 1.5 2
(b)
2 3
s2 Y (s) − sy(0) − y (0) + 4Y (s) = 3
+
s s−1
Substituindo-se os valores y(0) = 0 e y (0) = 2 obtemos
2 3
s2 + 4 Y (s) = 3
+ +2
s s−1
Assim,
2 3 2
Y (s) = + 2 + 4)
+ 2
s3 (s2 + 4) (s − 1)(s s +4
2 A B C Ds + E
= + 2+ 3+ 2
s3 (s2 + 4) s s s s +4
2 = As2 (s2 + 4) + Bs(s2 + 4) + C(s2 + 4) + (Ds + E)s3
= (A + D)s4 + (B + E)s3 + (4A + C)s2 + 4Bs + 4C
Comparando-se os termos de mesmo grau obtemos o sistema

 A
 + D = 0
B + E = 0



4A + C = 0
4B = 0




4C = 2


15. que tem solu¸ao A = −1/8, B = 0, C = 1/2, D = 1/8 e E = 0. Assim,
c˜
2 1/8 1 2 1 s
=− + 3+ 2
s3 (s2 + 4) s 4s 8s +4
3 A Bs + C
2 + 4)
= + 2
(s − 1)(s s−1 s +4
3 = A(s2 + 4) + (Bs + C)(s − 1) = (A + B)s2 + (−B + C)s + (4A − C)

 A + B = 0
− B + C = 0
4A − C = 3

que tem solu¸ao A = 3/5, B = −3/5 e C = −3/5. Assim,
c˜
3 3/5 3 s+1 3/5 3 s 3 2
= − 2 = − 2 −
(s − 1)(s 2 + 4) s−1 5s +4 s − 1 5 s + 4 10 s2 + 4
1/8 1 2 1 s 3/5 3 s 3 2 2
Y (s) = − + 3+ 2 + − 2 − 2+4
+ 2
s 4s 8 s + 4 s − 1 5 s + 4 10 s s +4
1 1 19 3 7
y(t) = − + t2 − cos 2t + et + sen 2t
8 4 40 5 10
16
y
14
12
10
8
6
4
2
0
x
−2
−0.5 0 0.5 1 1.5 2 2.5 3
(c)
1 4
s2 Y (s) − sy(0) − y (0) − 2 (sY (s) − y(0)) + Y (s) = 2
+
(s − 1) s

16. Substituindo-se os valores y(0) = 1 e y (0) = 1 obtemos
1 4
s2 − 2s + 1 Y (s) = + +s−1
(s − 1)2 s
Assim,
1 4 s−1
Y (s) = + +
(s − 1) 4 s(s − 1) 2 (s − 1)2
1 4 1
= 4
+ 2
+
(s − 1) s(s − 1) s−1
4 A B C
= + +
s(s − 1) 2 s s − 1 (s − 1)2
Multiplicando-se por s(s − 1)2 obtemos
4 = A(s2 − 2s + 1) + B(s − 1)s + Cs
Comparando-se os termos de mesmo grau obtemos o sistema

 A + B = 0
−2A − B + C = 0
A = 4

que tem solu¸ao A = 4, B = −4 e C = 4. Assim,
c˜
1 4 4 4 1
Y (s) = 4
+ − + 2
+
(s − 1) s s − 1 (s − 1) s−1
1 6 4 3 4
= + − +
6 (s − 1) 4 s s − 1 (s − 1)2
1
y(t) = t3 et + 4 − 3et + 4tet
6

17. 8
y
7
6
5
4
3
2
1
0
x
−1
−0.2 0 0.2 0.4 0.6 0.8
(d)
1
s2 Y (s) − sy(0) − y (0) − 2 (sY (s) − y(0)) − 3Y (s) = 3
(s − 2)2
Substituindo-se os valores y(0) = 1 e y (0) = 0 obtemos
1
s2 − 2s − 3 Y (s) = 3 +s−2
(s − 2)2
Assim,
1 s−2
Y (s) = 3 + 2
(s2 − 2s − 3)(s − 2)2 s − 2s − 3
1 s−2
= 3 2
+
(s − 3)(s + 1)(s − 2) (s − 3)(s + 1)
3
3 + (s − 2)
=
(s − 3)(s + 1)(s − 2)2
s3 − 6s2 + 12s − 5
=
(s − 3)(s + 1)(s − 2)2
A B C D
Y (s) = + + +
s − 3 s + 1 s − 2 (s − 2)2
Multiplicando-se Y (s) por (s − 3)(s + 1)(s − 2)2 obtemos
s3 − 6s2 + 12s − 5 =
A(s + 1)(s2 − 4s + 4) + B(s − 3)(s2 − 4s + 4) +
C(s2 − 2s − 3)(s − 2) + D(s2 − 2s − 3)

18. Comparando-se os termos de mesmo grau obtemos o sistema


 A + B + C = 1
−3A − 7B − 4C + D = −6


 16B + C − 2D = 12
4A − 12B + 6C − 3D = −5

Resolvendo-se o sistema por escalonamento obtemos a solu¸ao A = 1, B = 2/3,
c˜
C = −2/3 e D = −1. Assim,
1 2/3 2/3 1
Y (s) = + − −
s − 3 s + 1 s − 2 (s − 2)2
2 2
y(t) = e3t + e−t − e2t − te2t
3 3
9
y
8
7
6
5
4
3
2
1
0
x
−1
−0.2 0 0.2 0.4 0.6 0.8
(e)
2
s2 Y (s) − sy(0) − y (0) + 4Y (s) = 3
+4 s2
Substituindo-se os valores y(0) = 2 e y (0) = −1 obtemos
2
s2 + 4 Y (s) = 3 + 2s − 1
s2 + 4
Assim,
6 2s − 1
Y (s) = + 2
(s2 + 4) 2 s +4

19. 6 16 s 1
= 2 + 4)2
+2 2 − 2
16 (s s +4 s +4
3 8 s 1 2
= 2 + 4)2
+2 2 − 2
8 (s s +4 2s +4
3 1
y(t) = (sen 2t − 2t cos 2t) + 2 cos 2t − sen 2t
8 2
1 3
= 2 cos 2t − sen 2t − t cos 2t
8 4
2
y
1.5
1
0.5
0
x
−0.5
−1
−1.5
−2
−2.5
−3
−1 0 1 2 3 4 5 6
(f)
1 e−πs/2
s2 Y (s) − sy(0) − y (0) + Y (s) = −
s s
Substituindo-se os valores y(0) = 0 e y (0) = 1 obtemos
1 e−πs/2
s2 + 1 Y (s) = − +1
s s
Assim,
1 1 e−πs/2
Y (s) = + 2 −
s(s2 + 1) s + 1 s(s2 + 1)
1
= 2 + H(s) − e−πs/2 H(s),
s +1
em que
1
H(s) =
s(s2 + 1)

20. y(t) = sen t + h(t) − h(t − π/2)uπ/2 (t).
A Bs + C
+ 2
H(s) = .
s s +1
Multiplicando-se H(s) por s(s2 + 2s + 2) obtemos
1 = A(s2 + 1) + (Bs + C)s = (A + B)s2 + Cs + A

 A + B = 0
C = 0
A = 1

que tem solu¸ao A = 1, B = −1 e C = 0. Assim,
c˜
1 s
H(s) = − 2
s s +1
De onde obtemos que a fun¸ao cuja transformada de Laplace ´ H(s) ´
c˜ e e
h(t) = 1 − cos t
e a solu¸ao do problema de valor inicial ´ dado por
c˜ e
y(t) = sen t + h(t) − h(t − π/2)uπ/2 (t) = 1 − cos t + sen t − uπ/2 (t)(1 − sen t).
2.5
y
2
1.5
1
0.5
0
x
−0.5
−1
−1.5
−2
−2.5
−2 0 2 4 6 8 10 12
(g)
e−πs e−2πs
s2 Y (s) − sy(0) − y (0) + 2 (sY (s) − y(0)) + 2Y (s) = 2 −2
s s

21. Substituindo-se os valores y(0) = 0 e y (0) = 1 obtemos
e−πs − e−2πs
s2 + 2s + 2 Y (s) = 2 +1
s
Assim,
e−πs − e−2πs 1
Y (s) = 2 2 + 2
s(s + 2s + 2) s + 2s + 2
1
= (e−πs − e−2πs )H(s) + ,
(s + 1)2 + 1
em que
2
H(s) =
s(s2 + 2s + 2)
y(t) = h(t − π)uπ (t) − h(t − 2π)u2π (t) + e−t sen t.
A Bs + C
H(s) = + 2 .
s s + 2s + 2
Multiplicando-se H(s) por s(s2 + 2s + 2) obtemos
2 = A(s2 + 2s + 2) + (Bs + C)s = (A + B)s2 + (2A + C)s + 2A

 A + B = 0
2A + C = 0
2A = 2

que tem solu¸ao A = 1, B = −1 e C = −2. Assim,
c˜
1 s+2 1 s+2
H(s) = − 2 = −
s s + 2s + 2 s (s + 1)2 + 1
1 s+1 1
= − 2+1
−
s (s + 1) (s + 1)2 + 1
De onde obtemos que a fun¸ao cuja transformada de Laplace ´ H(s) ´
c˜ e e
h(t) = 1 − e−t cos t − e−t sen t
e a solu¸ao do problema de valor inicial ´ dado por
c˜ e
y(t) = h(t − π)uπ (t) − h(t − 2π)u2π (t) + e−t sen t.

22. 1.2
y
1
0.8
0.6
0.4
0.2
0
x
−0.2
−2 0 2 4 6 8 10 12
(h)
1 1
s2 Y (s) − sy(0) − y (0) + 4Y (s) = − e−2πs 2
+1 s2
s +1
Substituindo-se os valores y(0) = 0 e y (0) = 0 obtemos
1 e−2πs
s2 + 4 Y (s) = − 2
s2 + 1 s + 1
Assim,
1 e−2πs
Y (s) = −
(s2 + 1)(s2 + 4) (s2 + 1)(s2 + 4)
= H(s) − e−2πs H(s)
em que
1
H(s) =
(s2 + 1)(s2 + 4)
y(t) = h(t) − u2π (t)h(t − 2π)
As + B Cs + D
H(s) = + 2
s2 + 1 s +4
Multiplicando-se por (s2 + 1)(s2 + 4):
1 = (As + B)(s2 + 4) + (Cs + D)(s2 + 1)
= (A + C)s3 + (B + D)s2 + (4A + C)s + (4B + D)

23. Comparando-se os termos de mesmo grau obtemos o sistema

 A
 + C = 0
B + D = 0

 4A
 + C = 0
4B + D = 1

Resolvendo-se o sistema obtemos a solu¸ao A = 0, B = 1/3, C = 0 e D = −1/3.
c˜
Assim,
1/3 −1/3
H(s) = + 2
s2 + 1 s + 4
1 1
h(t) = sen t − sen 2t
3 6
1 1 1 1
y(t) = h(t) − u2π (t)h(t − 2π) = sen t − sen 2t − u2π (t)( sen t − sen 2t)
3 6 3 6
0.5
y
0.4
0.3
0.2
0.1
0
x
−0.1
−0.2
−0.3
−0.4
−0.5
−1 0 1 2 3 4 5 6 7 8 9
(i)
1 1
s2 Y (s) − sy(0) − y (0) + 4Y (s) = + e−πs 2
s2 + 1 s +1
Substituindo-se os valores y(0) = 0 e y (0) = 0 obtemos
1 e−πs
s2 + 4 Y (s) = + 2
s2 + 1 s + 1
Assim,
1 e−πs
Y (s) = + 2
(s2 + 1)(s2 + 4) (s + 1)(s2 + 4)
= H(s) + e−πs H(s)

24. em que
1
H(s) =
(s2 + 1)(s2 + 4)
y(t) = h(t) + uπ (t)h(t − π)
Do exerc´ anterior temos que
ıcio
1/3 −1/3
H(s) = + 2
s2+1 s +4
Assim,
1 1
h(t) = sen t − sen 2t
3 6
e portanto
1 1 1 1
y(t) = h(t) + uπ (t)h(t − π) = sen t − sen 2t − uπ (t)( sen t + sen 2t)
3 6 3 6
0.5
y
0.4
0.3
0.2
0.1
0
x
−0.1
−0.2
−0.3
−0.4
−0.5
−1 0 1 2 3 4 5 6 7 8 9
(j)
1 e−10s
s2 Y (s) − sy(0) − y (0) + 3 (sY (s) − y(0)) + 2Y (s) = −
s s
Substituindo-se os valores y(0) = 0 e y (0) = 0 obtemos
1 e−10s
s2 + 3s + 2 Y (s) = −
s s
Assim,
1 e−10s
Y (s) = 2 + 3s + 2)
− 2 + 3s + 2)
= H(s) − e−10s H(s)
s (s s (s

25. em que
1
H(s) =
s (s2 + 3s + 2)
y(t) = h(t) − u10 (t)h(t − 10).
1 1 A B C
H(s) = = = + +
s (s2 + 3s + 2) s(s + 1)(s + 2) s s+1 s+2
Multiplicando H(s) por s (s2 + 3s + 2) obtemos
1 = A s2 + 3s + 2 +Bs(s+2)+Cs(s+1) = (A+B+C)s2 +(3A+2B+C)s+2A

 A + B + C = 0
3A + 2B + C = 0
2A = 1

que tem solu¸ao A = 1/2, B = −1 e C = 1/2. Assim,
c˜
11 1 1 1
H(s) = − +
2s s+1 2s+2
1 1
h(t) = − e−t + e−2t
2 2
y(t) = h(t) − u10 (t)h(t − 10)
y
0.4
0.3
0.2
0.1
0
x
−0.1
0 5 10 15 20
(k)
e−2s
s2 Y (s) − sy(0) − y (0) + 3 (sY (s) − y(0)) + 2Y (s) =
s

26. Substituindo-se os valores y(0) = 0 e y (0) = 1 obtemos
e−2s
s2 + 3s + 2 Y (s) = +1
s
Assim,
1 e−2s
Y (s) = + = Y1 (s) + e−2s H(s)
s2 + 3s + 2 s (s2 + 3s + 2)
em que
1 1
H(s) = e Y1 (s) =
s (s2 + 3s + 2) s2 + 3s + 2
y(t) = y1 (t) − u2 (t)h(t − 2).
1 1 A B
Y1 (s) = = Y1 (s) = = +
s2 + 3s + 2 (s + 1)(s + 2) s+1 s+2
Multiplicando Y1 (s) por s2 + 3s + 2:
1 = A(s + 2) + B(s + 1) = (A + B)s + (2A + B)
A + B = 0
2A + B = 1
que tem solu¸ao A = 1 e B = −1. Assim,
c˜
1 1
Y1 (s) = −
s+1 s+2
y1 (t) = e−t − e−2t .
Do exerc´ anterior
ıcio
11 1 1 1
H(s) = − +
2s s+1 2s+2
1 1
h(t) = − e−t + e−2t
2 2
y(t) = y1 (t) + u2 (t)h(t − 2) = e−t − e−2t + u2 (t)h(t − 2)

27. y
0.4
0.3
0.2
0.1
0
x
−0.1
−2 0 2 4 6 8 10
(l)
e−3πs
s2 Y (s) − sy(0) − y (0) + Y (s) =
s
Substituindo-se os valores y(0) = 0 e y (0) = 1 obtemos
e−3πs
s2 + 1 Y (s) = +1
s
Assim,
e−3πs 1
Y (s) = 2 + 1)
+ 2
s(s s +1
1
= e−3πs H(s) + 2 ,
s +1
em que
1
H(s) =
s(s2 + 1)
y(t) = sen t + h(t − 3π)u3π (t).
A Bs + C
H(s) = + 2 .
s s +1
Multiplicando-se H(s) por s(s2 + 2s + 2) obtemos
1 = A(s2 + 1) + (Bs + C)s = (A + B)s2 + Cs + A

 A + B = 0
C = 0
A = 1


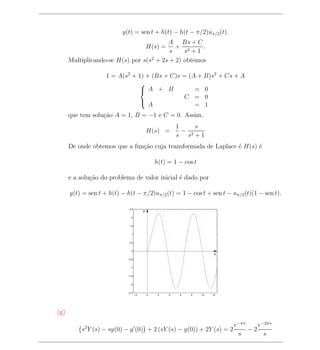
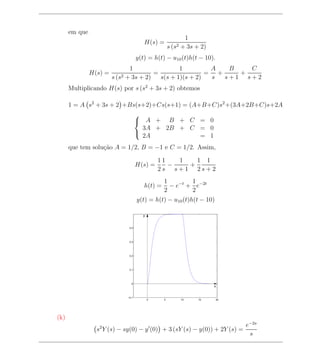
28. que tem solu¸ao A = 1, B = −1 e C = 0. Assim,
c˜
1 s
H(s) = − 2
s s +1
De onde obtemos que a fun¸ao cuja transformada de Laplace ´ H(s) ´
c˜ e e
h(t) = 1 − cos t
y(t) = sen t + h(t − 3π)u3π (t) = sen t + u3π (t)[1 − cos(t − 3π)]
2.5
y
2
1.5
1
0.5
0
x
−0.5
−1
−5 0 5 10 15 20 25
(m)
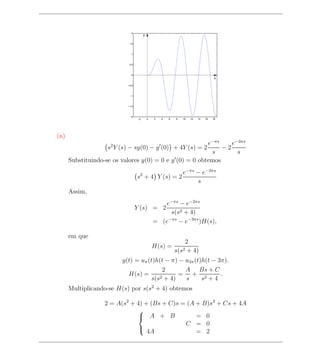
5 1 1
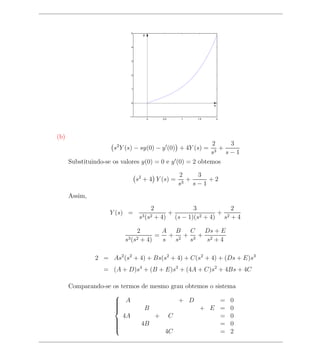
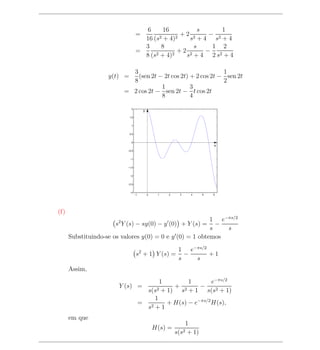
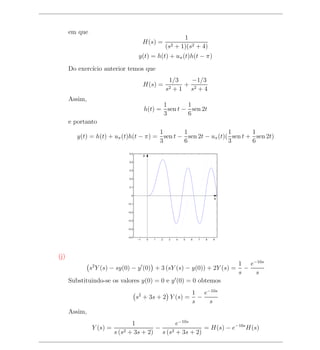
s2 Y (s) − sy(0) − y (0) + (sY (s) − y(0)) + Y (s) = 2 + e−πs 2
4 s +1 s +1
Substituindo-se os valores y(0) = 0 e y (0) = 0 obtemos
5 1 1
s2 + s + Y (s) = + e−πs 2
4 s2 + 1 s +1
Assim,
1 1
Y (s) = 5
+ e−πs 5
(s2
+ 1) s2 + s + 4
(s2 + 1) s2 + s + 4
= H(s) + e−πs H(s)
em que
1
H(s) = 5
(s2 + 1) s2 + s + 4

29. y(t) = h(t) + uπ (t)h(t − π)
1 As + B Cs + D
H(s) = = + 2
(s2 + 1) s2 + s + 5
4
s 2+1 s +s+ 5 4
5
Multiplicando-se H(s) por (s2 + 1) s2 + s + 4
:
5
1 = (As + B)(s2 + s + ) + (Cs + D)(s2 + 1)
4
5 5
= (A + C)s3 + (A + B + D)s2 + ( A + B + C)s + ( B + D)
4 4

 A
 + C = 0
A + B + D = 0

 5A +
 4 B + C = 0
5
B + D = 1

4
Resolvendo-se o sistema por escalonamento obtemos a solu¸ao A = −16/17,
c˜
B = 4/17, C = 16/17 e D = 12/17. Assim,
4 −4s + 1 4s + 3
H(s) = + 2
17 s 2+1 s +s+ 5 4
4 s 1 4s + 3
= −4 2 + 2 +
17 s + 1 s + 1 (s + 1/2)2 + 1
4 s 1 s + 3/4
= −4 2 + 2 +4
17 s +1 s +1 (s + 1/2)2 + 1
4 s 1 s + 1/2 1
= −4 2 + 2 +4 2+1
+
17 s +1 s +1 (s + 1/2) (s + 1/2)2 + 1
4
h(t) = −4 cos t + sen t + 4e−t/2 cos t + e−t/2 sen t
17
y(t) = h(t) + uπ (t)h(t − π)

30. 2
y
1.5
1
0.5
0
x
−0.5
−1
−1.5
−2
−2 0 2 4 6 8 10 12 14 16 18
(n)
e−πs e−3πs
s2 Y (s) − sy(0) − y (0) + 4Y (s) = 2 −2
s s
Substituindo-se os valores y(0) = 0 e y (0) = 0 obtemos
2 e−πs − e−3πs
s + 4 Y (s) = 2
s
Assim,
e−πs − e−2πs
Y (s) = 2
s(s2 + 4)
= (e−πs − e−3πs )H(s),
em que
2
H(s) =
s(s2 + 4)
y(t) = uπ (t)h(t − π) − u3π (t)h(t − 3π).
2 A Bs + C
H(s) = 2 + 4)
= + 2 .
s(s s s +4
Multiplicando-se H(s) por s(s2 + 4) obtemos
2 = A(s2 + 4) + (Bs + C)s = (A + B)s2 + Cs + 4A

 A + B = 0
C = 0
4A = 2


31. que tem solu¸ao A = 1/2, B = −1/2 e C = 0. Assim,
c˜
11 1 s
H(s) = −
2 s 2 s2 + 4
De onde obtemos que a fun¸ao cuja transformada de Laplace ´ H(s) ´
c˜ e e
1 1
h(t) = − cos 2t
4 4
y(t) = uπ (t)h(t − π) − u3π h(t − 3π)
y
0.4
0.3
0.2
0.1
0
x
−0.1
−2 0 2 4 6 8 10 12
(o)
s2 Y (s) − sy(0) − y (0) + Y (s) = e−2πs cos(2π)
Substituindo-se os valores y(0) = 0 e y (0) = 1 obtemos
s2 + 1 Y (s) = e−2πs + 1
Assim,
e−2πs 1
Y (s) = 2+1
+ 2
s s +1
e a solu¸ao do problema de valor inicial ´ dado por
c˜ e
y(t) = u2π (t) sen(t − 2π) + sen t = (u2π (t) + 1)sen t.

32. (p)
s2 Y (s) − sy(0) − y (0) + 4 (sY (s) − y(0)) + 4Y (s) = G(s)
Substituindo-se os valores y(0) = 2 e y (0) = −3 obtemos
s2 + 4s + 4 Y (s) = G(s) + 5 + 2s
Assim,
G(s) 5 + 2s
Y (s) = + 2
s2
+ 4s + 4 s + 4s + 4
G(s) 5 + 2s
= +
(s + 2) 2 (s + 2)2
5 + 2s A B
= +
(s + 2)2 s + 2 (s + 2)2
Multiplicando-se por (s + 2)2 obtemos
5 + 2s = A(s + 2) + B = As + (2A + B)
Comparando-se os termos de mesmo grau obtemos o sistema
A = 2
2A + B = 5
que tem solu¸ao A = 2 e B = 1. Assim,
c˜
G(s) 2 1
Y (s) = + +
(s + 2) 2 s + 2 (s + 2)2
y(t) = (e−2t t ∗ g)(t) + 2e−2t + e−2t t
t
= e−2(t−τ ) (t − τ )g(τ )dτ + 2e−2t + e−2t t
0
c˜ ıstica ´ r 2 − 6r + 8 = 0, que tem ra´ r1 = 2 e r2 = 4.
2. (a) A equa¸ao caracter´ e ızes
A equa¸ao homogˆnea correspondente tem solu¸ao geral
c˜ e c˜
y(t) = c1 e2t + c2 e4t .

33. Uma solu¸ao particular da equa¸ao n˜o homogˆnea ´ da forma yp (t) = A cos t+
c˜ c˜ a e e
B sin t. Substituindo-se yp (t), yp (t) e yp (t) na equa¸ao:
c˜
(7A − 6B) cos t + (6A + 7B) sin t = sin t
De onde obtemos A = 6/85 e B = 7/85. A solu¸ao geral da equa¸ao n˜o
c˜ c˜ a
homogˆnea ´
e e
6 7
y(t) = cos t + sin t + c1 e2t + c2 e4t
85 85
7
y (0) = 0 = + 2c1 + 4c2
85
6
y(0) = 0 = + c1 + c2
85
c1 = −1/10 e c2 = 1/34.
6 7 1 1
y(t) = cos t + sin t − e2t + e4t
85 85 10 34
(b)
1
s2 Y (s) − sy(0) − y (0) − 6 (sY (s) − y(0)) + 8Y (s) =
s2 + 1
Substituindo-se os valores y(0) = 0 e y (0) = 0 obtemos
1
s2 − 6s + 8 Y (s) =
s2 +1
Assim,
1
Y (s) =
(s2 − 6s + 8) (s2 + 1)
1 A B Cs + D
= + + 2
(s2 − 6s + 8) (s2 + 1) s−2 s−4 s +1
Multiplicando-se por (s2 − 6s + 8) (s2 + 1) obtemos
1 = A(s − 4)(s2 + 1) + B(s − 2)(s2 + 1) + (Cs + D)(s2 − 6s + 8)
= (A + B + C)s3 + (−4A − 2B − 6C + D)s2 +
+(A + B + 8C − 6D)s + (−4A − 2B + 8D)

34. Comparando-se os termos de mesmo grau obtemos o sistema


 A + B + C = 0
−4A − 2B − 6C + D = 0


 A + B + 8C − 6D = 0
−4A − 2B + 8D = 1

que tem solu¸ao A = −1/10, B = 1/34, C = 6/85 e D = 7/85. Assim,
c˜
1 1 1 1 6 s 7 1
Y (s) = − + + +
10 s − 2 34 s − 4 85 s 2−1 85 s2 − 1
1 2t 1 6 7
y(t) = − e + e4t + cos t + sin t
10 34 85 85

35. Referˆncias
e
[1] William E. Boyce and Richard C. DiPrima. Equa¸oes Diferenciais Elementares e
c˜
Problemas de Valores de Contorno. Livros T´cnicos e Cient´
e ıficos Editora S.A., Rio de
Janeiro, 7a. edition, 2002.
[2] Erwin Kreiszig. Matem´tica Superior. Livros T´cnicos e Cient´
a e ıficos Editora S.A., Rio
de Janeiro, 2a. edition, 1985.
[3] Dennis G. Zill and Michael R. Cullen. Equa¸oes Diferenciais. Makron Books, S˜o
c˜ a
Paulo, 3a. edition, 2001.