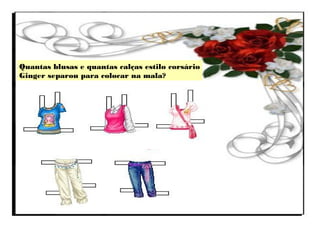
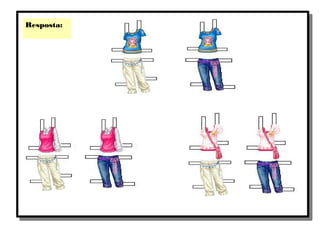
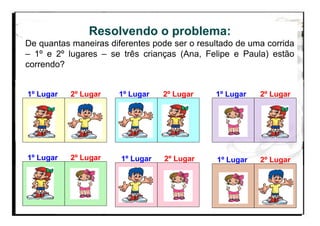
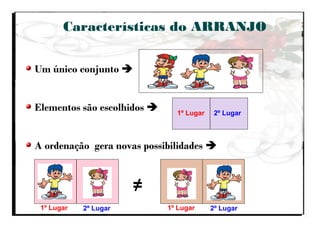
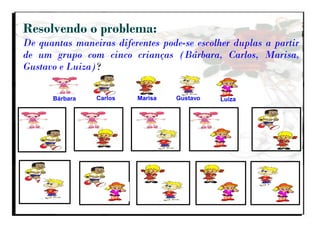
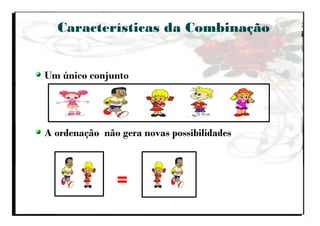
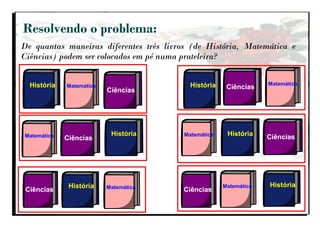
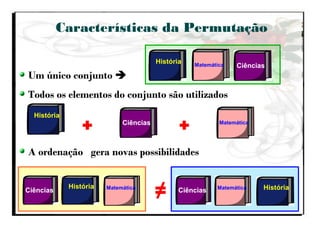
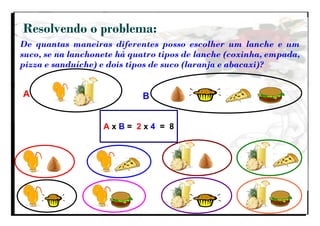
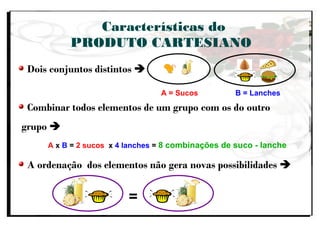
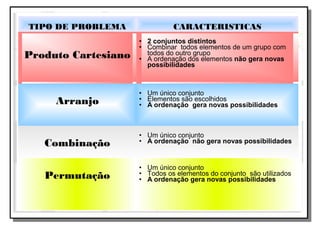
O documento aborda a importância do ensino de combinatória e probabilidade nos primeiros anos escolares, enfatizando a necessidade de superar a simples contagem e desenvolver estratégias mais complexas. Apresenta os quatro principais tipos de problemas combinatórios (arranjo, combinação, permutação e produto cartesiano) e discute as dificuldades enfrentadas por alunos nas etapas iniciais do aprendizado. A pesquisa destaca que, com o ensino adequado, as crianças podem entender e aplicar conceitos de combinatória de forma gradual e eficaz.

1. Superintendência Regional de Ensino de ItuiutabaSuperintendência Regional de Ensino de Ituiutaba
IXº Encontro – PNAIC MatemáticaIXº Encontro – PNAIC Matemática
““O Ensino de Combinatória e ProbabilidadeO Ensino de Combinatória e Probabilidade
Nos Primeiros Anos Escolares”Nos Primeiros Anos Escolares”
28 de março de 201528 de março de 2015

2. O ENSINO DE COMBINATÓRIA NOO ENSINO DE COMBINATÓRIA NO
CICLO DE ALFABETIZAÇÃOCICLO DE ALFABETIZAÇÃO
Cristiane Azevedo dos Santos PessoaCristiane Azevedo dos Santos Pessoa
Uma das primeiras aprendizagens matemáticas da criança consiste
em contar os elementos de diferentes conjuntos e enumerá-los para
determinar quantos são. Conhecida como a arte de contar, a
Combinatória, como um tipo de contagem, exige que seja superada
a ideia de enumeração de elementos isolados para se passar à
contagem de grupos de objetos, tendo como base o raciocínio
multiplicativo.
(Caderno 7 p.39)

3. Quantas blusas e quantas calças estilo corsário
Ginger separou para colocar na mala?

4. Quantas combinações de blusa e calça
Ginger pode fazer com estas roupas?

5. Resposta:

6. Na resolução de problemas pelas crianças observa-se que
uma das maiores dificuldades é a contagem de todas asmaiores dificuldades é a contagem de todas as
possibilidadespossibilidades. Isso ocorre porque o trabalho com a
Combinatória exige organização dos dados de modo
particular. Essa organização é realizada em níveis
diferenciados de abstração. Sabendo disso, podemos auxiliar
as crianças na sistematização de suas estratégias e no
desenvolvimento de ferramentas que podem ser úteis.
Maiores dificuldades das crianças...Maiores dificuldades das crianças...

7. ObservaçõesimportantesparaosProfessoresdo Ciclo daObservaçõesimportantesparaosProfessoresdo Ciclo da
AlfabetizaçãoAlfabetização
Uso de materiais manipulativos;
Situações com contextos próximos das
vivências das crianças;
O estimulo às diversas estratégias de resolução,
tais como desenhos, listagens ou árvores de
possibilidades;
Trabalho com problema que tenha número
total de possibilidades pequeno.

8. É uma parte da matemática que estuda os agrupamentos de elementos
sem precisar de enumerá-los.
A origem desse assunto está ligada ao estudo dos jogos de azar, tais
como: lançamento de dados, jogos de cartas, etc...
AnáliseCombinatória

9. Tipos de Problemas Combinatórios
Os problemas combinatórios normalmente trabalhados
na Educação Básica são de quatro tipos:
Arranjo
Combinação
Permutação
Produto Cartesiano
Uma característica comum a todos os tipos de problemas
é a necessidade de esgotar todas as possibilidades para se
chegar à resposta.

10. ARRANJO
De quantas maneiras diferentes pode ser o resultado de uma corrida –
1º e 2º lugares – se três crianças (Ana, Felipe e Paula) estão
correndo?
Esse tipo de problema caracteriza-se por ter apenas um conjunto a
partir do qual os elementos são escolhidos (no caso, o conjunto das
crianças) e a ordem de disposição dos elementos determina
possibilidades distintas. No problema citado há seis possibilidades
diferentes (AF, FA, FP, PF, AP e PA), considerando- -se que, por
exemplo, Ana em primeiro lugar e Felipe em segundo (AF) é diferente
de Felipe em primeiro lugar e Ana em segundo (FA).
(Texto: Salto para o Futuro p.7)
Ana Felipe Paula

11. Resolvendo o problema:
De quantas maneiras diferentes pode ser o resultado de uma corrida
– 1º e 2º lugares – se três crianças (Ana, Felipe e Paula) estão
correndo?
1º Lugar 2º Lugar 1º Lugar 2º Lugar 1º Lugar 2º Lugar
1º Lugar 2º Lugar 1º Lugar 2º Lugar 1º Lugar 2º Lugar

12. Características do ARRANJO
Um único conjunto 
Elementos são escolhidos 
A ordenação gera novas possibilidades 
1º Lugar 2º Lugar
1º Lugar 1º Lugar2º Lugar 2º Lugar
≠

13. Fórmula do Arranjo Simples
Ao trabalharmos com arranjos simples, com n elementos distintos,
agrupados p a p, com p ≤ n, podemos recorrer à seguinte fórmula:
A = n!
(n-p)!
No problema apresentado teríamos: n= 3 p=2
A = 3! = 3 x 2x1 = 6 = 6
(3-2)! 1! 1
n,pn,pn,p
3,2
Ao produto dos números naturais começando em n e decrescendo até 1 denominamos de fatorial de n e
representamos por n!.
Segundo tal definição, o fatorial de 5 é representado por 5! e lê-se 5 fatorial.
5! é igual a 5 . 4 . 3 . 2 . 1 que é igual a 120, assim como 4! é igual a 4 . 3 . 2 . 1 que é igual a 24, como 3! é igual a
3 . 2 . 1 que é igual a 6 e que 2! é igual a 2 . 1 que é igual a 2.
Por definição tanto 0!, quanto 1! são iguais a 1.

14. COMBINAÇÃO
De quantas maneiras diferentes pode-se escolher duplas a
partir de um grupo com cinco crianças (Bárbara, Carlos,
Marisa, Gustavo e Luiza)?
Nesse tipo de problema, a escolha também é a partir de um
conjunto único (como nos arranjos), mas a ordem de disposição dos
elementos não determina possibilidades distintas: a dupla Bárbara
e Gustavo (BG) é igual à dupla Gustavo e Bárbara (GB), por
exemplo. Tem-se, nesta situação, dez possibilidades: BC, BG, BM,
BS, CG, CM, CS, GM, GS e MS.
(Texto: Salto para o Futuro p.7)
Bárbara Carlos Marisa Gustavo Luiza

15. Resolvendo o problema:
De quantas maneiras diferentes pode-se escolher duplas a partir
de um grupo com cinco crianças (Bárbara, Carlos, Marisa,
Gustavo e Luiza)?
Bárbara Carlos Marisa Gustavo Luiza

16. Características da Combinação
Um único conjunto
A ordenação não gera novas possibilidades
=

17. Fórmula da Combinação Simples
Ao trabalharmos com combinações simples, com n elementos distintos,
agrupados p a p, com p ≤ n, podemos recorrer à seguinte fórmula:
C = n!
p!(n-p)!
No problema apresentado teríamos: n= 5 p=2
C = 5! = 5! = 5x4x3! = 20 = 10
2!(5-2)! 2!x3! 2! x 3! 2 x 1
n,pn,pn,p
5,2
Ao produto dos números naturais começando em n e decrescendo até 1 denominamos de fatorial de n e
representamos por n!.
Segundo tal definição, o fatorial de 5 é representado por 5! e lê-se 5 fatorial.
5! é igual a 5 . 4 . 3 . 2 . 1 que é igual a 120, assim como 4! é igual a 4 . 3 . 2 . 1 que é igual a 24, como 3! é igual a
3 . 2 . 1 que é igual a 6 e que 2! é igual a 2 . 1 que é igual a 2.
Por definição tanto 0!, quanto 1! são iguais a 1.

18. PERMUTAÇÃO
Permutação: De quantas maneiras diferentes três livros (de
História, Matemática e Ciências) podem ser colocados em pé
numa prateleira?
A permutação é um caso particular de arranjo. As escolhas
são feitas a partir de um conjunto único, com a diferença de
que todos os elementos do conjunto são utilizados, sendo a
ordem diferenciada, o que identifica cada possibilidade. Nesse
caso, há seis maneiras distintas de colocar os três livros em
uma prateleira: HMC, HCM, MHC, MCH, CHM e CMH.
(Texto: Salto para o Futuro p.7)
História Matemática Ciências

19. Resolvendo o problema:
De quantas maneiras diferentes três livros (de História, Matemática e
Ciências) podem ser colocados em pé numa prateleira?
História Matemática
Ciências
Matemática
Ciências
História
Ciências
História Matemática
História Matemática
Ciências
Matemática
Ciências
História Matemática
CiênciasHistória
Ciências
HistóriaMatemática

20. Características da Permutação
Um único conjunto 
Todos os elementos do conjunto são utilizados
A ordenação gera novas possibilidades
Ciências
História
MatemáticaCiências
Ciências
História Matemática
Ciências HistóriaMatemática
 
História Matemática
≠

21. Fórmula da Permutação Simples
A cada um dos agrupamentos que podemos formar com certo número de elementos
distintos, tal que a diferença entre um agrupamento e outro se dê apenas pela
mudança de posição entre seus elementos, damos o nome de permutação simples.
Neste caso o agrupamento de livros ( matemática, história, ciências ), difere do
agrupamento ( história, ciências, matemática ), pois embora os elementos de ambos
os grupos sejam os mesmos, há mudança no posicionamento de ao menos um dos
seus elementos.
Para resolver este problema podemos recorrer à fórmula: P = n!
No problema apresentado teríamos: n = 3
P = 3!  P = 3x 2x 1  P = 6n 3 3
n

22. PRODUTO CARTESIANO
O produto cartesiano de dois conjuntos A e B são todos os pares
ordenados (x, y), sendo que x pertence ao conjunto A e y pertence ao
conjunto B.
O produto cartesiano de A por B é igual a: AxB
Vejamos um problema que envolve análise combinatória com Produto
Cartesiano
De quantas maneiras diferentes posso escolher um lanche e
um suco, se na lanchonete há quatro tipos de lanche (coxinha,
empada, pizza e sanduíche) e dois tipos de suco (laranja e
abacaxi)?
Nesse tipo de problema, as escolhas são efetuadas a partir de
distintos conjuntos de elementos (no caso, o conjunto de lanches e
o conjunto de sucos)

23. Resolvendo o problema:
De quantas maneiras diferentes posso escolher um lanche e um
suco, se na lanchonete há quatro tipos de lanche (coxinha, empada,
pizza e sanduíche) e dois tipos de suco (laranja e abacaxi)?
A B
A x B = 2 x 4 = 8

24. Características do
PRODUTO CARTESIANO
Dois conjuntos distintos 
Combinar todos elementos de um grupo com os do outro
grupo 
A ordenação dos elementos não gera novas possibilidades 
A = Sucos B = Lanches
A x B = 2 sucos x 4 lanches = 8 combinações de suco - lanche
=

25. TIPO DE PROBLEMA CARACTERISTICAS
Produto Cartesiano
• 2 conjuntos distintos
• Combinar todos elementos de um grupo com
todos do outro grupo
• A ordenação dos elementos não gera novas
possibilidades
Arranjo
• Um único conjunto
• Elementos são escolhidos
• A ordenação gera novas possibilidades
Combinação
• Um único conjunto
• A ordenação não gera novas possibilidades
Permutação
• Um único conjunto
• Todos os elementos do conjunto são utilizados
• A ordenação gera novas possibilidades

26. Pessoa e Borba (2009) realizaram uma pesquisa de sondagem com
alunos da Educação Básica, observando o desempenho de
educandos do 2º e 3º Anos ao resolverem dois problemas
combinatórios de cada tipo (Arranjo; Combinação; Permutação e
Produto Cartesiano). Essa pesquisa demonstrou que estas crianças
conseguem perceber características dos problemas combinatórios.
Porém, os alunos do 2º Ano ainda apresentam dificuldade em
esgotar todas as possibilidades. Já os alunos do 3º Ano conseguem
chegar ao final das resoluções, mesmo quando os resultados são
maiores que 20.
(PNAIC, Caderno 7 – Educação Estatística, p. 42)

27. Se problemas variados de Combinatória forem
trabalhados desde os anos iniciais do Ensino
Fundamental, por meio de representações
simbólicas apropriadas e que possibilitem
uma gradual construção de procedimentos
mais formais, aumenta-se a possibilidade de se
chegar ao uso consciente das fórmulas de
Análise Combinatória no Ensino Médio.
(PNAIC, Caderno 7 – Educação Estatística, p.50)

28. Onde quer que haja mulhes e homens,
Há sempre o que fazer,
Há sempre o que ensinar,
Há sempre o que aprender.
Paulo Freire