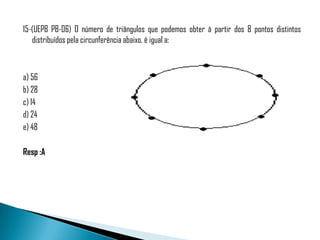
Este documento discute conceitos de análise combinatória, incluindo princípio de contagem, fatorial, arranjo simples, permutação simples, combinação simples, permutações com elementos repetidos e permutações circulares, ilustrando cada conceito com exemplos numéricos.