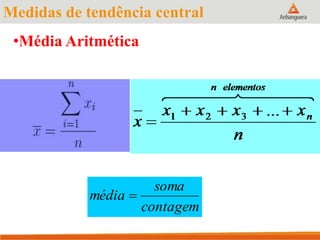
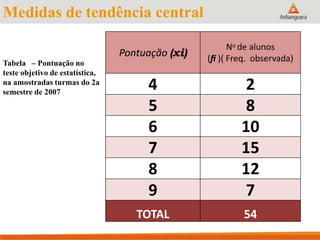
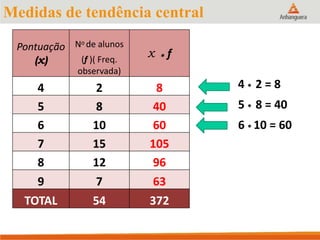
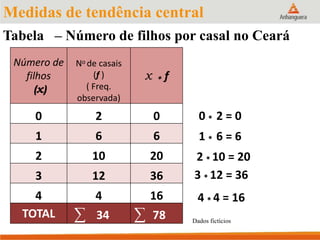
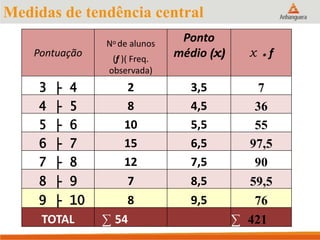
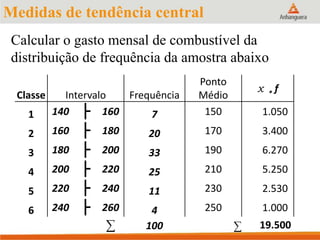
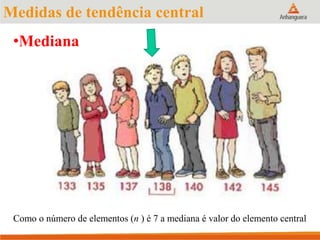
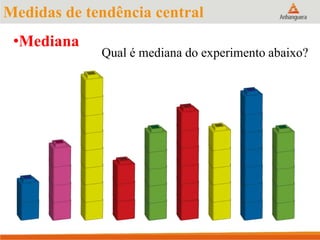
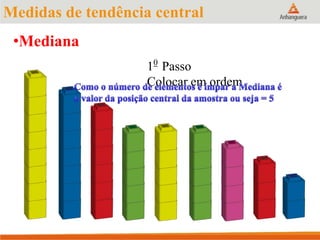
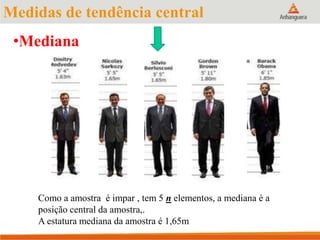
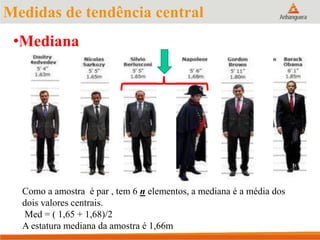
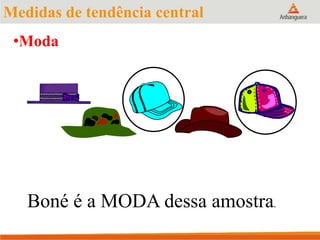
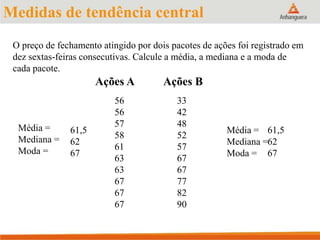
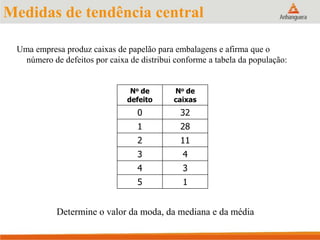
Este documento apresenta um resumo sobre medidas de tendência central em estatística, incluindo média, mediana e moda. Explica como calcular cada medida e fornece exemplos para ilustrar os cálculos. Também fornece referências adicionais para estudos sobre o tema.