Geometria espacial de posição
•Transferir como PPT, PDF•
4 gostaram•7,387 visualizações
Denunciar
Compartilhar
Denunciar
Compartilhar
Mais conteúdo relacionado
Mais procurados
Mais procurados (20)
8 ano-angulos-retas-paralelas-cortadas-por-uma-transversal-3

8 ano-angulos-retas-paralelas-cortadas-por-uma-transversal-3
Destaque
Destaque (8)
Semelhante a Geometria espacial de posição
Semelhante a Geometria espacial de posição (20)
Geométria espacial autor antonio carlos carneiro barroso

Geométria espacial autor antonio carlos carneiro barroso
Mais de ELIZEU GODOY JR
Mais de ELIZEU GODOY JR (19)
Último
Último (20)
O que é arte. Definição de arte. História da arte.

O que é arte. Definição de arte. História da arte.
Cópia de AULA 2- ENSINO FUNDAMENTAL ANOS INICIAIS - LÍNGUA PORTUGUESA.pptx

Cópia de AULA 2- ENSINO FUNDAMENTAL ANOS INICIAIS - LÍNGUA PORTUGUESA.pptx
Slides Lição 6, CPAD, As Nossas Armas Espirituais, 2Tr24.pptx

Slides Lição 6, CPAD, As Nossas Armas Espirituais, 2Tr24.pptx
Considerando as pesquisas de Gallahue, Ozmun e Goodway (2013) os bebês até an...

Considerando as pesquisas de Gallahue, Ozmun e Goodway (2013) os bebês até an...
Educação Financeira - Cartão de crédito665933.pptx

Educação Financeira - Cartão de crédito665933.pptx
Polígonos, Diagonais de um Polígono, SOMA DOS ANGULOS INTERNOS DE UM POLÍGON...

Polígonos, Diagonais de um Polígono, SOMA DOS ANGULOS INTERNOS DE UM POLÍGON...
Slides Lição 6, Betel, Ordenança para uma vida de obediência e submissão.pptx

Slides Lição 6, Betel, Ordenança para uma vida de obediência e submissão.pptx
aula de bioquímica bioquímica dos carboidratos.ppt

aula de bioquímica bioquímica dos carboidratos.ppt
Introdução às Funções 9º ano: Diagrama de flexas, Valor numérico de uma funçã...

Introdução às Funções 9º ano: Diagrama de flexas, Valor numérico de uma funçã...
Poesiamodernismo fase dois. 1930 prosa e poesiapptx

Poesiamodernismo fase dois. 1930 prosa e poesiapptx
Geometria espacial de posição
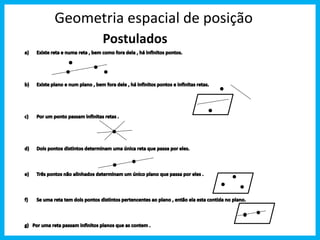
- 1. Geometria espacial de posição Postulados
- 2. Posições relativas entre duas retas Retas não coplanares ou reversas: não existe plano que as contem ao mesmo tempo Paralelas distintas r s rs Paralelas coincidentes r s r s Concorrentes r s rs {P} P Obliquas r s Ortogonais r s rs Retas coplanares : existe plano que as contem ao mesmo tempo
- 3. Posições relativas entre reta e plano Reta contida no plano Concorrente ou secante ao plano r r P r {P} r {r} Reta paralela ao plano r r Obs : reta fura o plano
- 4. Observações : Reta perpendicular ou ortogonal ao plano r Reta paralela ao plano r
- 5. Posições relativas entre dois planos Concorrentes Paralelas Coincidentes r {r}
- 6. Geometria Espacial Poliedros Prof: ELIZEU
- 7. Poliedros Prof: ELIZEU - A superfície de um poliedro é formada por polígonos, chamados FACES do poliedro; - Os lados dos polígonos são chamados ARESTAS do poliedro; - Os vértices dos polígonos são os VÉRTICES do poliedro.
- 8. Poliedros Prof: ELIZEU Num poliedro convexo uma aresta é sempre comum a apenas duas faces Num poliedro convexo cada face esta contida em planos diferentes
- 9. Relação de Euller . V + F = A + 2 Obs1: Válido para todo poliedro convexo Prof: ELIZEU
- 10. Prof: ELIZEU Ex1: Um poliedro convexo possui 12 faces e 8 vértices. Determine o número de arestas desse poliedro. Ex2: Um poliedro convexo possui exatamente 4 faces pentagonais e 6 faces triangulares. Determine o número de vértices desse sólido.
- 11. Poliedros de Platão Existem apenas cinco poliedros de Platão: - Tetraedro; - Hexaedro; -Octaedro; -Dodecaedro; -Icosaedro. Prof: ELIZEU Obs2: Se um poliedro convexo possui todas as faces formadas por polígonos regulares e congruentes, então ele é chamado de POLIEDRO REGULAR.
