O documento descreve que o vetor (1, 0, 0) gera o subespaço unidimensional correspondente à reta horizontal no plano cartesiano R2. Além disso, explica que qualquer vetor em R3 pode ser escrito como uma combinação linear dos vetores da base canônica {(1,0,0), (0,1,0), (0,0,1)}.

1. Qual o subespaço gerado pelo vetor
(1, 0, 0) , ou seja, [ (1, 0, 0) ] ?

2. { ( 1, 0, 0 ) , ( 0,1, 0 ) , ( 0, 0,1) }
3
é um conjunto de Geradores para R
Porque todo vetor ( x, y, z ) ∈ R
3
Pode ser escrito da forma:
( x, y, z ) = x ( 1,0,0 ) + y ( 0,1,0 ) + z ( 0,0,1)
Assim, escrevemos:
R =  ( 1,0,0 ) , ( 0,1,0 ) , ( 0,0,1) 
3
 

3. (1, 0) = e1 Vetor canônico, gerador da
reta horizontal
(0,1) = e2 Vetor canônico, gerador da
reta vertical
( 5,0) = 5 ⋅ (1,0)
∈ [ e1 ] ∈ [ e1 , e2 ]
(−1,0) = −1 ⋅ (1,0)
( 0, −3) = −3 ⋅ (0,1)
(0, 2) = 2 ⋅ (0, 2)
∈ [ e2 ]
(2,3) = 2 ⋅ (1, 0) + 3 ⋅ (0,1)
123 123
∈[ e1 ] ∈[ e2 ]

4. ( a, b)
R = [ e1 , e2 ]
e2 = ( 0 ,1) 2
e1 = (1, 0 )
pois ∀ (a, b)∈ R 2
(a, b) = a (1,0) + b (0,1)
R = [ e1 , e2 , (2,0)] pois ∀ (a, b)∈ R
2 2
(a, b) = a (1,0) + b (0,1) + 0.(2,0)

5. E por que estes 2 conjuntos
têm quantidades diferentes de
geradores, se são geradores
do mesmo espaço?

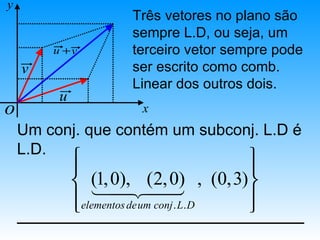
6. Os elementos chamados geradores ou
sistemas de geradores de V podem
ser um conjunto L.I ou L.D.
R = [ e1 , e2 ]
2 { e1 , e2 } Conj. L.I
R = [ e1 , e2 , (2,0)] { e1 , e2 , (2,0)} Conj. L.D
2

7. Dependência e não dependência Linear
y u
y r r
v = αu
u
v
v
o y x
o x
r r
u +v
u +v
v Depende
r r
de u e v
u
o x

8. Um ponto representa o vetor nulo.
Vetor qualquer
 Um único vetor diferente do vetor
nulo é sempre L.I
 Dois vetores são L.D quando um
é múltiplo por um escalar do outro
u u = (1, 0)
v v = 2u
v = (2, 0)

9. y
Três vetores no plano são
sempre L.D, ou seja, um
u +v terceiro vetor sempre pode
v ser escrito como comb.
Linear dos outros dois.
u
o x
Um conj. que contém um subconj. L.D é
L.D.

 

 (1, 0),244 , (0,3) 
14 4
(2, 0)
3
elementos deum conj . L. D
 


10. De um conjunto L.D podemos extrair um
subconjunto. L.I
 Se um conjunto é L.I, todos os seus
subconjuntos são L.I
 Um conjunto que possui o vetor nulo é sempre
L.D.

11. - conjunto ordenado:
- formado por um conjunto de vetores L.I.
- gera V.
Proposição: De um conjunto de geradores
de um espaço ou subespaço vetorial V é
sempre possível extrair uma base.

12. Processo prático para determinar uma
base de um subespaço do ¡ .
n
Consiste em escalonar a matriz cujas linhas
são os vetores geradores do subespaço.
As linhas que não “zerarem” correspondem
aos vetores geradores que forem LI.
Determinar uma base para o seguinte
2
subespaço do espaço do R :
W =  ( 1,1) , ( 1,0 ) , ( 0, − 1) 
 

13. 1 1  1 1 
A =  1 0  uuuuuuuuuuuuur
 
L2 ↔ L2 − L1u
u
 0 −1
L2 → − Lu
  uuuuuuuuuu2
r
 0 − 1
   0 −1
 
1 1   1 0
 0 1  B = { ( 1,1) , (0,1)}
L1 → L1 − Lu
uuuuuuuuuuuuu
r
0 1  2
  L3 → L3 + Lu   ( BASE )
uuuuuuuuuuuuur2
 0 0
 0 − 1
   
Portanto, os vetores (1,1) e (1,0)
(correspondentes às linhas que não se
anularam na matriz escalonada) formam a
base para W.

14. Dimensão
Proposição: Seja V um espaço vetorial
finitamente gerado. Então, qualquer base
de V tem o mesmo número de elementos
(cardinalidade).
A este número de elementos dá-se o
nome de Dimensão de V.
Portanto, se V é finitamente gerado,
podemos dizer que ele tem
dimensão finita.

15. Resultados importantes
Seja V um espaço de dimensão finita n. Então:
 Qualquer conjunto com mais de n elementos
em V é LD.
 Qualquer conjunto L.I de V pode ser completado
para formar uma base de V.
 Qualquer conjunto L.I de V tem no máximo n
elementos.
 Qualquer conjunto L.I com n elementos é uma
base de V.

16. Dimensão da Soma de 2 Subespaços
Seja V um espaço vetorial de dimensão
finita e U, W subespaços de V. Então
dim ( U + W ) = dim U + dim W − dim ( U ∩ W )

17. Determine um conjunto de geradores, a
base e a dimensão para os seguintes
subespaços:
a ) U = { ( x, y, z ) ∈ R ; x − y − z = 0}
3
b) V = { ( x, y, z ) ∈ R ; x − 2 y = 0}
3
c) U + V
d )U ∩ V

18. ( x, y , z ) ∈ V ⇔
x− y−z =0
Ou seja, x= y+z
Assim, um genérico vetor de U é da forma:
( y + z, y, z )
y (1,1, 0) + z (1, 0,1)
Assim:
U = [ (1,1, 0) , (1, 0,1) ]

19. U=[(1,1,0),(1,0,1)].
(1,1, 0) não é múltiplo de (1, 0,1)
O conjunto { (1,1, 0), (1, 0,1)} é L.I
Logo constitui uma base para o
subespaço U
Assim dim(U ) = 2

20. ( x, y , z ) ∈ V ⇔
x − 2y = 0
Ou seja, x = 2 y e z é qualquer.
Assim, um genérico vetor de V é da forma:
(2 y, y, z ) = y (2,1, 0) + z (0, 0,1)
V = [ (2,1, 0) , (0, 0,1)]

21. V = [ (2,1, 0) , (0, 0,1) ]
(2,1, 0) não é múltiplo de (0, 0,1)
O conjunto { (2,1, 0), (0, 0,1)} é L.I
Logo constitui uma base para o
subespaço V
Assim dim(V ) = 2

22. Um conjunto de geradores para U+V è
dado pela uniao dos dois conjuntos, i.e.,:
U = [ (1,1, 0) , (1, 0,1) ]
V = [ (2,1, 0) , (0, 0,1)]
U + V = [(1,1, 0) , (1, 0,1), (2,1, 0), (0, 0,1)]
Para extrair uma base usaremos o processo
prático de determinação de uma base.

23. U + W =  ( 1,1,0 ) , ( 1,0,1) , ( 2,1,0 ) , ( 0,0,1) 
 
1 1 0 1 1 0
1  L2 → L2 − L1 0 −1 
1
 0 1 
2 1 0  L3 → L3 − 2 L1 0 −1 0
   
0 0 1 0 0 1
L2 → − L2
 1 1 0 1 0 1
0 1 −1 L1 → L1 − L2 0 
 1 −1
 
0 −1 0  L3 → L3 + L2 0 0 0
   
0 0 1 0 0 1

24. U + W =  ( 1,1,0 ) , ( 1,0,1) , ( 2,1,0 ) , ( 0,0,1) 
 
{ (1,1, 0), (1, 0,1), (0, 0,1)}
Constituem uma base para U +W
1 0 1 Ou ainda
0 
1 −1

0 0 0 { (1, 0,1), (0,1, −1), (0, 0,1)}
 
0 0 1 (Vetores restantes)
dim (U + V ) = 3

25. Precisamos encontrar um conjunto de vetores que
satisfaça a ambas as condições:
x − y − z = 0

x − 2 y = 0 ⇒ x = 2 y
Substituindo na 1ª equação temos:
2y − y − z = 0 ⇒ y − z = 0 ⇒ y = z
(2 y, y, y ) = y (2,1,1)
U ∩ V = [ (2,1,1) ] ⇒ dim(U ∩ V ) =1

26. Portanto, utilizando a relação podemos
coomprovar a dimensão do espaço soma.
dim(U + W ) = dim U + dim W − dim (U ∩ W )
dim ( U + V ) = 2 + 2 − 1 = 3

28. { ( 1, 0, 0 ) , ( 0,1, 0 ) , ( 0, 0,1) }
3
é um conjunto de Geradores para R
R =  ( 1,0,0 ) , ( 0,1,0 ) , ( 0,0,1) 
3
 
e é linearmente independente (L.I)
Logo { ( 1, 0, 0 ) , ( 0,1, 0 ) , ( 0, 0,1) }
É uma base de R3
Como possui 3 elementos, Dim R3 = 3

29. O vetor u = (1, −3,5)pode ser escrito da
seguinte forma:
u = 1(1, 0, 0) − 3(0,1, 0) + 5(0, 0,1)
Portanto, dizemos que o vetor u é
uma combinação linear dos vetores
(1, 0, 0) , (0,1, 0), (0, 0,1)
com os escalares 1, -3, 5 (coord. do vetor)

30. r r r r
v = ( 1,-3,5 ) = 1i - 3j + 5k
r
i = ( 1,0,0 )
5k
r P
j = ( 0,1,0 ) r
k v
r j -3j
k = ( 0,0,1 ) i o
r r r
{
β = i , j, k } 1i
[ v] β = (1, −3,5)

31. Se mudássemos a base de referência
r r r
{
β = i , j, k }
ou
β = { (1, 0, 0), (0,1, 0), (0, 0,1)}
As coordenadas dos vetores
continuariam a mesma?

32. V =R 3
Encontre as coordenadas do vetor
v = ( 1, − 3,5 )
Na base B = { ( 1,1,1) , ( 1,0,1) , ( 1,0, − 1) }
'

33. B = { ( 1,1,1) , ( 1,0,1) , ( 1,0, − 1) }
'
Por definição, às coordenadas de v na
base B´ é dado pelos coeficientes a,b e c
abaixo:
( 1, − 3,5) = a ( 1,1,1) + b ( 1,0,1) + c ( 1,0, − 1)

34. ( 1, − 3,5) = a ( 1,1,1) + b ( 1,0,1) + c ( 1,0, − 1)
⇓
a +b + c = 1

a = −3 ⇒ a = −3
a +b −c = 5


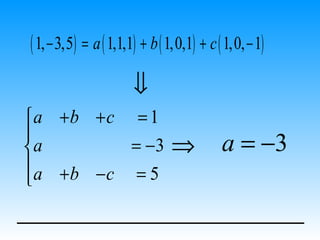
35. b + c = 4
 ⇒ 2b = 12 ⇒ b = 6
b − c = 8
⇓
c = −2 ⇐ 6+c = 4
As coordenadas de v são -3,6 e -2
 −3
A matriz das coordenadas 6
de v na base B´ é [ v] B ' = 
 −2 
 

36. As coordenadas de v dependem da
base B escolhida e da ordem dos de
seus elementos.

37. Bibliografia Básica
ANTON, H.; RORRES, C.: Álgebra Linear com
Aplicações. Bookman, 8ª ed.
Porto Alegre: RS, 2001.
CALLIOLI, C. A.; DOMINGUES,
HYGINO H.; COSTA, Roberto C. F.
Álgebra Linear e Aplicações. Atual, 7ª
ed. São Paulo: SP, 2000.
HOFFMAN, K.;KUNZE,R.: Álgebra Linear. LTC
editora, 1979