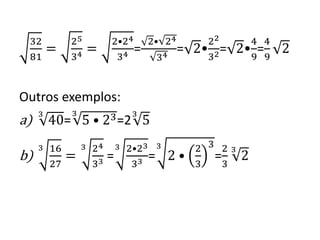1) O documento explica como passar fatores para dentro e para fora de radicais. 2) É possível decompor números inteiros nos seus fatores primos e usar essa decomposição para mover fatores entre o radicando e o exterior do radical. 3) A regra para mover um fator é dividir seu expoente pelo índice da raiz.

1. Passar um factor para dentro do radical
Da expressão 2 7a=2• 7a;
onde 2 e 7a são factores
O factor 2 chama-se coeficiente
7a é radicando
A operação efectuada é multiplicação, só que por
convenção não se escreve o sinal de multiplicação
(entre 2 e 7a assim como entre 7 e a.

2. Agora presta atênção á seguinte explicação:
2• 7𝑎= 2
2
• 7𝑎
= 22• 7𝑎
= 7𝑎 • 22
= 4 • 7𝑎

3. De acordo com a regra da multiplicação de
raízes quadradas.
Conforme a explicação dada no exemplo
anterior qualquer número pode ser escrito na
forma de um radical de índice n.
Por exemplo podemos escrever o número 5 na
forma de radical.
De índice 2, fica: 5=
2
5; de índice 6, fica 5=
6
5

4. Com base no que acabamos de afirmar, é
possível, dada uma expressão do tipo a
n
b
passar a para factor do radicando,isto é, para
dentro do radical, assim como se mostra:
a
n
b=
𝑛
𝑎 𝑛 • 𝑏

5. Consideremos a expressão:
3 2 Vamos passar o coeficiente (factor) três
(3) para dentro do radical.
Para passar o factor 3 para dentro do radical em
3 2, vamos fazer como se mostra na caixa de
generalização anterior.
3 2= 32 • 2= 9 • 2= 18

6. Outros exemplos:
𝑎) 32
5= 32 2 • 5= 34 • 5= 81 • 5= 405
b) 𝑎3
•p•x4
a7= 𝑎7 • 𝑎3 2 • 𝑝1 2 • x4 2
= 𝑎7 • 𝑎6 • 𝑝2 • x8
= 𝑎13 • 𝑝2 • x8

7. Passagem de um factor de dentro para fora do
radical
Para passar o factor de dentro para fora do
radical, tem que saber como decompor um
número inteiro em factores primos.
Com efeito, apresentamos já a seguir alguns
aspectos fundamentais à aprendizagem desta
lição.

8. Para melhor compreender esta lição primeiro
deve rever o conceito e a definição sobre
decomposição de números inteiros em factores
primos.
Números primos são todos números que
admitem apenas dois divisores, a unidade e o
próprio número.
Exemplo de números primos
{2;3;5;7;11;13;17;19;23;29;31;37;41;47;...}

10. Para os casos em que se tem letras ou se
apresenta na forma de potência, pode se
representar como se segue:
𝑎6
= 𝑎 • 𝑎 • 𝑎 • 𝑎 •a•a
𝑚7
=m•m•m•m•m•m•m
𝑥3
=x•x•x
25
=2•2•2•2•2

11. Passagem de Factores do Radicando para fora
do radical
Considere: 25 ; porque o índice da raíz é 2 ,
podemos decompor o radicando em potências
de expoente igual ou inferir ao índice da raíz.
25 = 22 • 22 • 2= 22• 22 • 2

12. Pela regra do produto de raízes quadradas e porque
22 = 2. Assim:
25 = 2 • 2 • 2=22
2
Pode-se concluir que:
Na passagem de um factor do radicando para fora
do radical, divide-se o expoente do radicando pelo
índice da raíz. O quociente desta divisão fica
expoente do factor que sai e o resto, o expoente do
factor que fica no radicando.

13. Por outro lado para a 25, usando a regra
prática, onde é necessário tomar em
consideração que o índice da raiz é 2.
Assim teremos:
Na Prática

14. Daqui se conclui que: 25=22
2=4 2
Atenção:
Na decomposição dos radicandos deve-se
observar que os factores a considerar, devem ser
aqueles que produzem um expoente igual ao
índice do radical.

15. Consideremos o radical:
32
81
, passemos os
factores possíveis para fora do radical.
Para tal seguiremos o mesmo procedimento
como no caso anterior. Só que desta vez
devemos tomar em consideração que o
radicando é um número fraccionário.
Sendo assim deve-se decompor o numerador e
o denominador.

16. 32
81
=
25
34 =
2•24
34 =
2• 24
34
= 2•
22
32= 2•
4
9
=
4
9
2
Outros exemplos:
a)
3
40=
3
5 • 23=2
3
5
b)
3 16
27
=
3 24
33 =
3 2•23
33 =
3
2 •
2
3
3
=
2
3
3
2