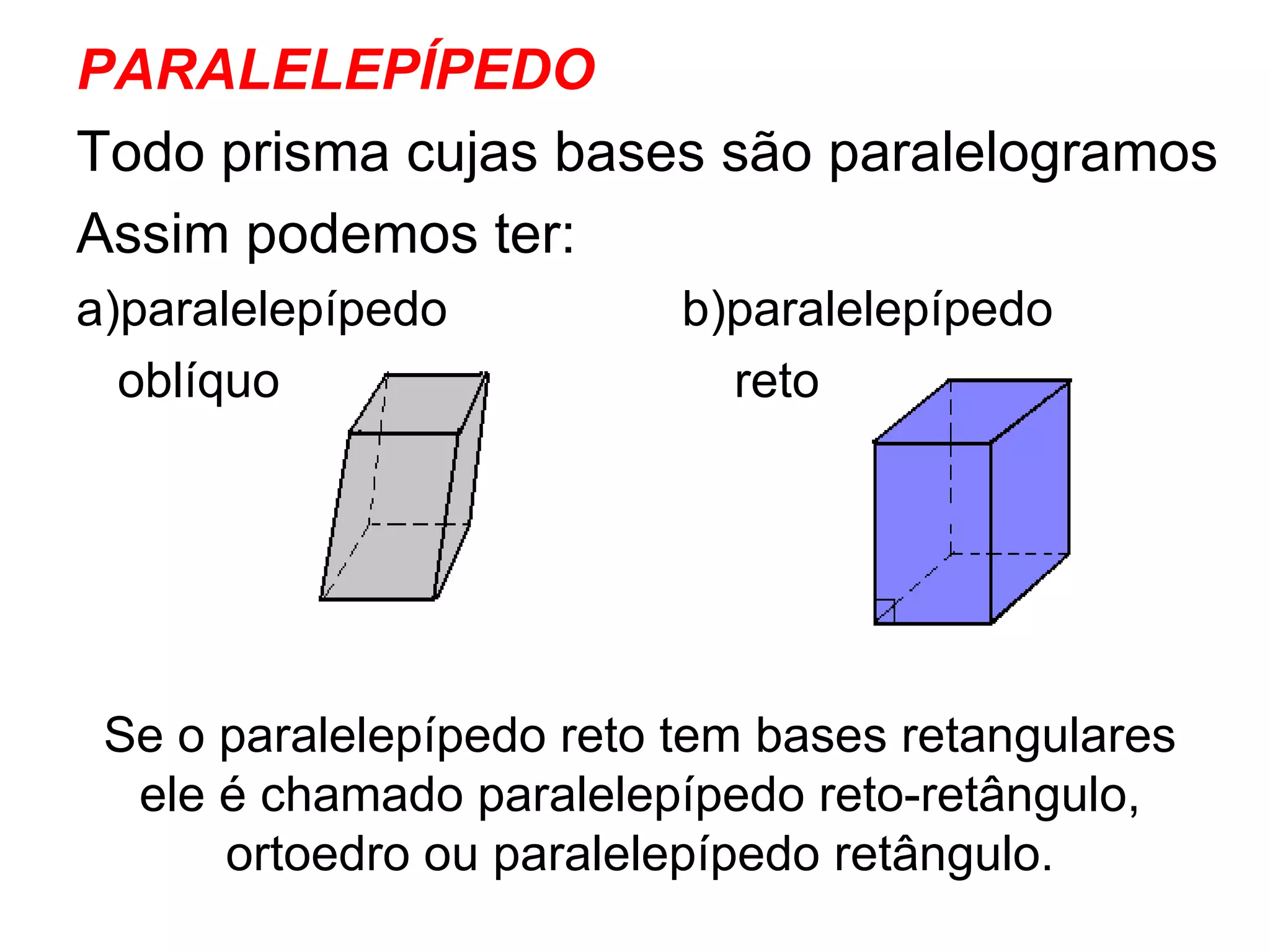
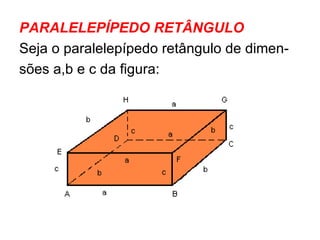
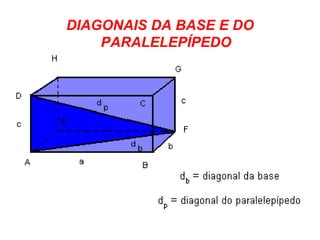
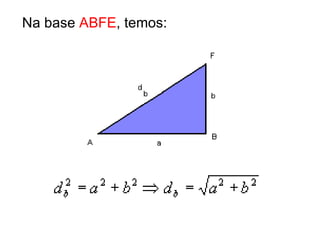
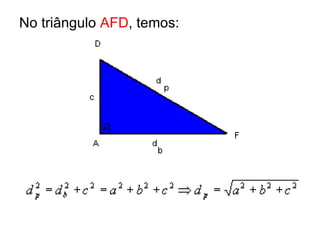
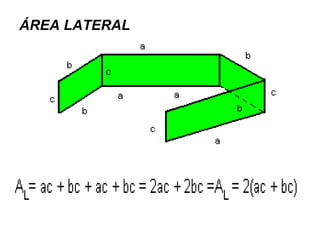
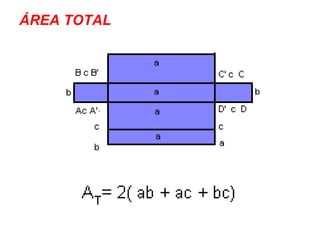
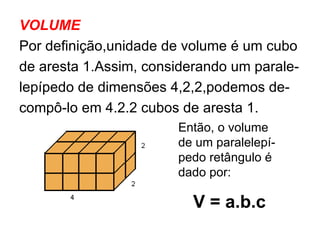
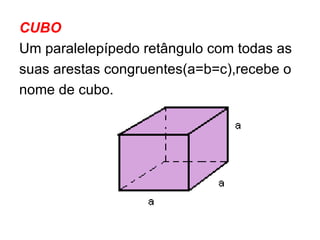
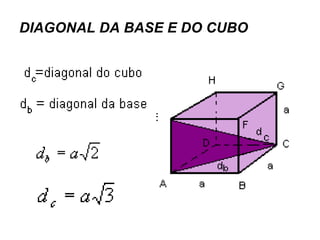
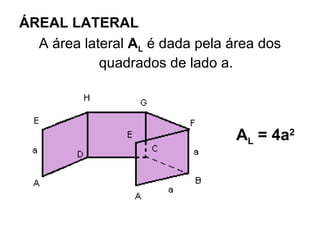
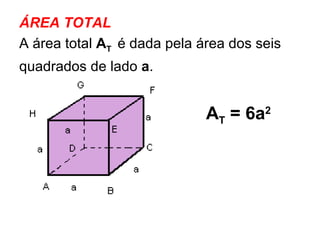
O documento descreve as propriedades geométricas do paralelepípedo e do cubo. Explica que um paralelepípedo é um prisma cujas bases são paralelogramos e pode ser reto ou oblíquo. Um paralelepípedo reto-retângulo tem bases retangulares. Fornece fórmulas para calcular a área lateral, área total e volume de um paralelepípedo retângulo e cubo. Inclui também exercícios resolvidos como exemplos.

1. PARALELEPÍPEDO Todo prisma cujas bases são paralelogramos Assim podemos ter: a)paralelepípedo b)paralelepípedo oblíquo reto Se o paralelepípedo reto tem bases retangulares ele é chamado paralelepípedo reto-retângulo, ortoedro ou paralelepípedo retângulo.

2. PARALELEPÍPEDO RETÂNGULO Seja o paralelepípedo retângulo de dimen- sões a,b e c da figura:

3. DIAGONAIS DA BASE E DO PARALELEPÍPEDO

4. Na base ABFE , temos:

5. No triângulo AFD , temos:

6. ÁREA LATERAL

7. ÁREA TOTAL

8. VOLUME Por definição,unidade de volume é um cubo de aresta 1.Assim, considerando um parale- lepípedo de dimensões 4,2,2,podemos de- compô-lo em 4.2.2 cubos de aresta 1. Então, o volume de um paralelepí-pedo retângulo é dado por: V = a.b.c

9. EXERCÍCIO RESOLVIDO Página 391- (R 2 ) As dimensões,comprimento,largura e altura, de um paralelepípedo reto-retângulo são 20 cm,12cm e 9 cm.Calcule a medida de uma diagonal desse paralelepípedo. R 3 )Calcular a área total de um paralelepípedo reto-retângulo cujas dimensões,comprimento largura e altura são 6m,5m e 2m.

10. EXERCÍCIO RESOLVIDO Página 392 – (R 4 ) Calcular o volume V de um paralelepípedo reto-retângulo de área total 198 cm 2 e de dimensões diretamente proporcionais a 1,2 e 3.

11. CUBO Um paralelepípedo retângulo com todas as suas arestas congruentes(a=b=c),recebe o nome de cubo.

12. DIAGONAL DA BASE E DO CUBO

13. ÁREAL LATERAL A área lateral A L é dada pela área dos quadrados de lado a. A L = 4a 2

14. ÁREA TOTAL A área total A T é dada pela área dos seis quadrados de lado a . A T = 6a 2

15. VOLUME De forma semelhante ao volume ao paralele pípedo retângulo,o volume de um cubo de aresta a , é dado por: V = a.a.a = a 3

16. EXERCÍCIO RESOLVIDO Página 393 – (R 5 ) Sabendo que uma diagonal de uma face de Um cubo mede 5√2 cm ,calcular,desse cubo A medida de uma diagonal; b) A área total; c) O volume ATIVIDADE PROPOSTA Página 393 e 394(exercício 3 ao 11)