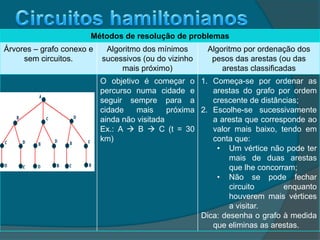
O documento define e explica conceitos básicos sobre grafos, incluindo suas partes constituintes (vértices e arestas), tipos de grafos (conexo, digrafo, completo), características dos vértices (grau, par ou ímpar) e problemas relacionados a grafos (euleriano, hamiltoniano). Também apresenta métodos para resolver esses problemas, como algoritmos para encontrar caminhos mínimos ou árvores geradoras.

1. Por: Joana Pinto

2. São representações esquemáticas
constituídas por conjuntos finitos de pontos
(vértices) e por segmentos (arestas), que
unem os pontos.
No quotidiano, os grafos são utilizados para
encontrar soluções ótimas para
determinadas situações: na definição de
redes de distribuição de mercadorias, na
organização de roteiros, na definição de
horários ou de sequências de tarefas.

3.  Grafo conexo1 – grafo onde existe sempre uma
sequência de arestas a unir quaisquer dois dos seus
vértices.
 Digrafo (ou grafo orientado)2 – grafo em que as
arestas têm orientações (sentidos) definidas (com
setas).
 Grafo completo3 – grafo em que cada um dos
vértices é adjacente a todos os outros.
Por exemplo, o grafo 3 é de ordem 5 pois tem 5
vértices
1
2 3

4.  Grau (ou valência) de um vértice é o número de
arestas que nele concorrem. Diz-se que um vértice
tem grau par se nele concorre um número par de
arestas e que tem grau ímpar no caso de esses
números ser ímpar.
 Passeio – sequência de vértices em que cada dois
vértices consecutivos estão ligados por uma
aresta, podendo haver repetição;
 Caminho – passeio em que apenas se passa uma
vez em cada vértice;
 Trajeto (ou trilho) – é um passeio em que apenas
se passa uma vez por cada aresta;
 Circuito (ou ciclo) – é um caminho que começa e
acaba no mesmo vértice.

5. Trajeto euleriano – percorre todas as arestas e
um grafo uma única vez.
 Regra: Num grafo conexo, podemos encontrar um
trajeto euleriano se e só se existirem, no máximo,
dois vértices de grau ímpar.
Circuito euleriano – é um trajeto euleriano (ou
seja, percorre todas as arestas do grafo uma
única vez) que começa e acaba no mesmo
vértice
 Regra: Num grafo conexo podemos encontrar um
circuito euleriano se e só se todos os vértices
tiverem grau par.
Problemas eulerianos – problemas que
envolvem as arestas de um grafo.

6. Eulerização de grafos – eulerizar um grafo
consiste em acrescentar-lhe arestas, por forma a
tornar possível encontrar um circuito euleriano.
Se pretendermos eulerizar um grafo, devemos:
1. Verificar o grau de cada vértice para localizar
os que têm grau ímpar;
2. Adicionar arestas sempre com o objetivo de
que todos os vértices fiquem com grau par.
No entanto, adicionar arestas corretamente significa
que só podemos duplicar uma aresta já existente
entre dois vértices. A melhor eulerização é sempre
aquela que acrescenta o menor número de arestas.

7. Circuito hamiltoniano é um caminho que
começa e acaba no mesmo vértice
percorrendo todos os vértices uma só
vez. Um grafo diz-se hamiltoniano se
nele se pode encontrar, pelo menos, um
circuito hamiltoniano.
Pesos – número que se atribui a cada
uma das arestas de um grafo. Pode
representar distâncias, custos, tempo,
etc. A um grafo com pesos atribuídos
chamamos grafo ponderado.

8. Métodos de resolução de problemas
Árvores – grafo conexo e
sem circuitos.
Algoritmo dos mínimos
sucessivos (ou do vizinho
mais próximo)
Algoritmo por ordenação dos
pesos das arestas (ou das
arestas classificadas
(Com valores e totais)
O objetivo é começar o
percurso numa cidade e
seguir sempre para a
cidade mais próxima
ainda não visitada
Ex.: A  B  C (t = 30
km)
1. Começa-se por ordenar as
arestas do grafo por ordem
crescente de distâncias;
2. Escolhe-se sucessivamente
a aresta que corresponde ao
valor mais baixo, tendo em
conta que:
• Um vértice não pode ter
mais de duas arestas
que lhe concorram;
• Não se pode fechar
circuito enquanto
houverem mais vértices
a visitar.
Dica: desenha o grafo à medida
que eliminas as arestas.

9.  Árvore abrangente (ou árvore geradora)
é uma árvore que contém todos os
vértices de um grafo dado.
 Árvore abrangente mínima – árvore
em que a soma dos pesos das arestas
é mínima.
 Nos tipos de problemas que compreendem
as árvores abrangentes mínimas, não temos
de regressar ao ponto de partida: só temos
de encontrar um percurso que visite todos
os vértices sem criar circuitos. Por isso, os
vértices podem ter tantas retas a concorrer-
lhes quantas necessárias.

10. Para descobrir a árvore abrangente
mínima num grafo existe o Algoritmo de
Kruskal.
Algoritmo de Kurskal: Vão-se unindo as
arestas do grafo por ordem crescente
dos pesos, desde que não formem
circuitos e se garanta que no final todos
os vértices estão na árvore.

11. Caminho crítico é uma
sequência de tarefas que
deve ser realizada no tempo
previsto, de forma que
determinado trabalho ou
projeto seja concretizado
dentro do prazo. A sua
duração é aquela que
determina o menor tempo
para a conclusão do projeto e
corresponde à maior duração
global
Tarefa Tempo (dias) Dependências
T1 1 Nenhuma
T2 2 T1
T3 3 T2
T4 4 T2
T5 5 T2
T6 7 T3 e T5
T7 6 T4 e T5
T8 8 T5
T9 9 T8

12.  Crescimento populacional positivo: há
um aumento da população;
 Crescimento populacional negativo: há
uma diminuição/declínio da população
 Crescimento contínuo – as mudanças
acontecem a todo o instante;
 Crescimento discreto – as mudanças
acontecem de tempos a tempos e
sempre que se dá uma mudança, diz-se
que ocorreu uma transição

13. Progressão aritmética – sucessão em que a
diferença entre transições é constante, à
qual chamamos razão, r, da progressão.
No caso de crescimento populacional, a
razão representa a taxa de crescimento da
população.
Modelo de crescimento linear discreto: é
um modelo em que a evolução da
população é descrita por uma progressão
aritmética (Pn + 1 – Pn = r)  diferença
entre cada termo e o anterior é constante.
Para um modelo linear discreto:
Pn = P0 + n x r ou y = ax + b