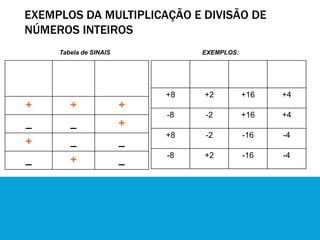
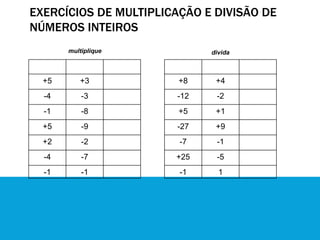
1) O documento apresenta as regras de sinais para realizar operações com números inteiros, incluindo adição, subtração, multiplicação e divisão. 2) São explicadas as regras de sinais para adição e subtração, onde o sinal do resultado segue o sinal do número de maior valor absoluto. 3) Para multiplicação e divisão, o sinal do resultado é positivo quando os sinais forem iguais e negativo quando forem diferentes.

1. MATEMÁTICA DO GENTE
Professor Marcelo Lorio

2. Descritor 01.Efetuar cálculos com números inteiros, envolvendo
as operações de adição, subtração, multiplicação, divisão e/ou
potenciação.
Você já sabe fazer essas contas, não é mesmo?
8 + 2 = 10
8 – 2 = 6
8 x 2 = 16
8 : 2 = 4
Agora ,vejamos essas outras :
-8 -2 = -10 -8 x -2 = +16 8 x -2 = -16 -8 : -2 = +4 -8 : 2 = -4
2 – 8 = -6 -8 x 2 = -16 8 : -2 = -4
Note que alguns resultados mudaram de sinal. Por isso, é importante que
aprendamos as
Regras de Sinais para sabermos Somar, Diminuir, Multiplicar e Dividir
números inteiros. Vamos lá?

3. REGRAS DE SINAIS PARA A ADIÇÃO E
SUBTRAÇÃO de números inteiros.
Adição e Subtração :
Na adição ou na subtração, quando os números possuirem sinais contrários,
iremos manter o sinal do número que possuir o MAIOR VALOR ABSOLUTO.
Exemplos :
i)+2 +4 = +6 (Somas desse tipo já aprendemos! Claro, o resultado é sempre
positivo!)
ii)(+3) + (-8) = -5 ( O sinal é o mesmo do número com MAIOR VALOR
ABSOLUTO, no caso, o sinal de -8).
iii)3 -8 = -5 ( Note que essa conta é a mesma do item acima. Por quê?)
iv)-3 – 5 = -8 ( Perceba que os números , quando possuem sinais iguais,o
resultado seguirá o sinal dos números. Foi o que aconteceu também no item i).
VAMOS EXERCITAR UM POUCO?

4. EXERCÍCIOS de fixação
1.Efetue
a)+7 +3 = f) +2 +11 +3 =
b)-7 + 3 = g) -3 -5 -10 =
c)-7 – (+3) = h) +4 -11 +2 -4 =
d)-7 + (-3) = i) (-7) + (3) –(-4) + (5) =
e)-7 -3 = j) -7 +3 +4 +5 =
OBS : -(-x) = + x. Por exemplo : -(-3) = +3
Observe os itens i e j. O que você pode concluir ?

5. REGRAS DE SINAIS DA MULTIPLICAÇÃO E
DIVISÃO DE NÚMEROS INTEIROS.
A REGRA É BASTANTE SIMPLES :
Números com sinais iguais o resultado da multiplicação ou
divisão
terá :
SINAL POSITIVO.
Números com sinais diferentes o resultado da multiplicação ou
divisão terá:
SINAL NEGATIVO.
VAMOS AOS EXEMPLOS :

6. EXEMPLOS DA MULTIPLICAÇÃO E DIVISÃO DE
NÚMEROS INTEIROS
Tabela de SINAIS
Sinal X Sinal Y Resultado
X.Y ou X/Y
+ + +
_ _ +
+ _ _
_ + _
EXEMPLOS:
X Y X.Y X/Y
+8 +2 +16 +4
-8 -2 +16 +4
+8 -2 -16 -4
-8 +2 -16 -4

7. EXERCÍCIOS DE MULTIPLICAÇÃO E DIVISÃO DE
NÚMEROS INTEIROS
multiplique
X Y X.Y
+5 +3
-4 -3
-1 -8
+5 -9
+2 -2
-4 -7
-1 -1
divida
X Y X/Y
+8 +4
-12 -2
+5 +1
-27 +9
-7 -1
+25 -5
-1 1

8. Expressões Numéricas
Agora iremos resolver expressões que possuem contas de somar,
diminuir, multiplicar e dividir. Para isso, podemos seguir algumas
estratégias. Vejamos :
1)Estratégia do agrupamento :
Exemplo : Efetue a expressão : +2 -3 +5 +7 -5 -8 -12 + 10. Agrupamos os
números com sinais positivos e os números com sinais negativos. Teremos
(+2 +5 +7 +10) e (-3 -5 -8 – 12). Obtemos os resultados de cada
agrupamento, ou seja, (+24) e (-28). Agora basta somarmos os dois
agrupamentos :
(+24) + (-28) = 24 – 28 = -4. Fácil, não é mesmo?

9. Expressões Numéricas
2) Estratégia da redução por pares :
Exemplo : Efetue +2 -3 +5 -7. Reduzimos as 4 parcelas em
duas :
(+2 -3) + (+5 -7) = (-1) + (-2) = -3
OBS: Com a prática você irá resolver em um processo
direto, somando e subtraindo conforme a ordem dos
números.

10. Expressões Numéricas
Mas como poderemos resolver uma expressão como
essa ?
8 + { 7 - [ (+4) . (-2) + 4 ] – 3 }
Devemos seguir algumas regras :
1º) Resolver todas as raízes e/ou potências;
2º) As operações de multiplicação e/ou divisão;
3º) Adição e subtração;
Sempre seguindo a ordem:
1º) Resolver tudo o que se encontra dentro dos
parênteses ( );
2º) Em seguida o que está dentro do colchete [ ];
3º) E, por último, o que está dentro da chave { }

11. Expressões numéricas
8 + { 7 - [ (+4) . (-2) + 4 ] – 3 }.
•Resolvemos primeiro o que está dentro dos colchetes, começando pela
MULTIPLICAÇÃO. [ (-8) + 4 ] = [-4].
•Agora vamos resolver o que ficou entre chaves , que é uma SOMA DE
INTEIROS: {7 – [-4)]– 3} = {7 +4 -3} = 8
•Finalmente, somaremos o resultado encontrado com o 8 que está fora das
chaves. Portanto, o resultado final será : 8 + 8 =16.