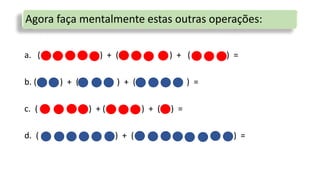
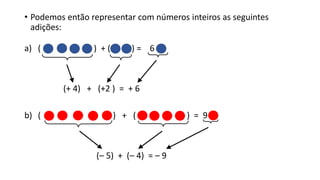
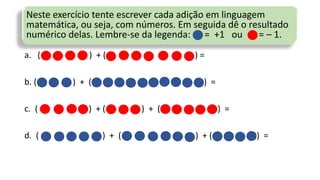
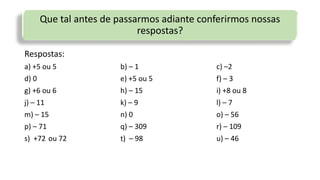
O documento discute operações com números inteiros positivos e negativos, começando com adição e subtração. Ele apresenta exemplos usando bolas azuis e vermelhas para representar números positivos e negativos, respectivamente, e ensina a técnica do cancelamento para simplificar operações. O documento também fornece respostas para exercícios propostos.

1. Operações com números
inteiros positivos e negativos.
Adição e subtração.
Professor Adriano Augusto
Rede Municipal de Ensino de Belo Horizonte - MG

2. Adição de números inteiros:
• Antes das operações com esses números preste atenção às seguintes
situações e tente respondê-las mentalmente:
• ( ) + ( ) =
• ( ) + ( ) =

3. Agora confira se você acertou.
• ( ) + ( ) = 5 ou Cinco bolas azuis.
• ( ) + ( ) = 7 ou sete bolas vermelhas.

4. Agora faça mentalmente estas outras operações:
a. ( ) + ( ) + ( ) =
b. ( ) + ( ) + ( ) =
c. ( ) + ( ) + ( ) =
d. ( ) + ( ) =

5. Confira seus acertos.
a. 12
b. 9
Simples assim!
c. 8
d. 14

6. Vamos agora convencionar o seguinte:
• Legenda:
a) = +1 ou seja, uma bola azul equivale a um positivo.
Então:
= + 3 (três bolas azuis equivalem a +3.)
b) = – 1 ou seja, uma bola vermelha equivale a um negativo.
Do mesmo modo:
= – 5 (cinco bolas vermelhas equivalem a – 5).

7. • Podemos então representar com números inteiros as seguintes
adições:
a) ( ) + ( ) = 6
(+ 4) + (+2 ) = + 6
b) ( ) + ( ) = 9
(– 5) + (– 4) = – 9

8. a. ( ) + ( ) =
b. ( ) + ( ) =
c. ( ) + ( ) + ( ) =
d. ( ) + ( ) + ( ) =
Neste exercício tente escrever cada adição em linguagem
matemática, ou seja, com números. Em seguida dê o resultado
numérico delas. Lembre-se da legenda: = +1 ou = – 1.

9. Confira seus resultados antes de passar adiante!
a. (– 4) + (– 7) = –11 ou 11 .
b. (+ 3) + (+ 10) = 13 ou + 13 ou ainda 13 .
c. (– 4) + (– 3) + (– 5) = –12 ou 12 .
d. (+ 5) + (+6) + (+ 4) = 15 ou + 15 ou ainda 15 .

10. Podemos então pensar em somar bolas de cores diferente.
Antes vamos combinar o seguinte: uma bola azul com uma bola
vermelha se cancelam (dá resultado zero), e vice-versa, ou seja:
• ( ) + ( ) = 0 ou em linguagem matemática: (–1) + (+1) = 0.
Do mesmo modo:
• ( ) + ( ) = 0, ou seja, (+3) + (–3) = 0.
• Agora é sua vez, represente em linguagem matemática e dê o
resultado de:
• ( ) + ( ) =
• ( ) + ( ) =

11. • Veja como podemos usar isso a nosso favor na adição de bolas de
cores diferentes ou de números inteiros de sinais contrários:
• ( ) + ( ) =
• Com o traço estamos cancelando uma bola vermelha com uma
azul, ou vice versa. Essa é a técnica do cancelamento.
• Prosseguindo com essa ação:
• ( ) + ( ) =
• Do mesmo modo, podemos pensar na técnica do cancelamento para
números:
• (–5) + (+3) = (–2 –3) + (+3) = – 2
Preste atenção à maneira como reescrevemos o –5 = –2 –3.

12. Agora tente exercitar sem as bolas coloridas! Use e abuse da
técnica do cancelamento.
1) Efetue as seguintes adições:
a) (+7) + (- 2) = b) (- 3) + (+ 2) = c) (+4) + (- 6) =
d) (+5) + (- 5) = e) (+1) + (+ 4) = f) (- 2) + (- 1) =
g) 7 + (- 1) = h) - 6 + (- 9) = i) +3 + (+ 5) =
j) (-10) + (- 1) = k) (+1) + (- 10) = l) (- 3) + (- 4) =
m) (- 7) + (- 8) = n) (+12) + (- 12) = o) (- 32) + (- 24) =
p) (+27) + (- 98) = q) (- 735) + (+426) = r) (- 17) + (- 92) =
s) (+ 74) + (- 6) = t) (- 56) + (- 42) = u) – 74 + ( +28) =

13. Que tal antes de passarmos adiante conferirmos nossas
respostas?
Respostas:
a) +5 ou 5 b) – 1 c) –2
d) 0 e) +5 ou 5 f) – 3
g) +6 ou 6 h) – 15 i) +8 ou 8
j) – 11 k) – 9 l) – 7
m) – 15 n) 0 o) – 56
p) – 71 q) – 309 r) – 109
s) +72 ou 72 t) – 98 u) – 46

14. Antes da subtração, vamos trabalhar o conceito de número
oposto ou simétrico como “ o contrário de”!
Por exemplo:
O contrário de uma bolinha azul é uma bolinha vermelha, que indicamos:
– ( ) = ou em linguagem matemática: – (+1) = –1.
Do mesmo modo:
O contrário de uma bolinha vermelha é uma bolinha azul.
– ( ) = ou em linguagem matemática: – (–1) = +1.
Pelo que acabamos de ver, a maneira de indicarmos o simétrico ou o
contrário de um número é colocando o sinal de menos “–” na frente desse
número.
/

15. Vamos exercitar um pouco mais isso que acabamos de ver!
Pelo que combinamos anteriormente, teremos então:
a. – ( ) = ( ) ou seja: – (+3) = ( – 3).
b. – ( ) = ( ) ou seja: – (– 2) = (+2).
Agora tente representar matematicamente as seguintes situações:
– ( ) = ( ) ou seja: – (___) =(___).
– ( ) = ( ) ou seja: – (___) = (___).

16. Chegamos finalmente onde precisávamos: a subtração.
Veja como enxergar a subtração de números inteiros a partir de nossas
convenções anteriores:
a. ( ) – ( ) = que ficará assim:
( ) + ( ) = Em seguida vamos usar a técnica do
cancelamento.
( ) + = Ou em números:
(+2 +3) + (– 3) = 2 ou +2

17. Veja agora a subtração entre números de sinais contrários a partir da
nossa convenção:
( ) – ( ) = que ficará assim:
Lembre-se que o contrário de bolas azuis são
bolas vermelhas.
( ) + ( ) = – 10
(– 3) + (– 7) = – 10
Que tal agora nos livrarmos da bolas azuis e vermelhas e passarmos
diretamente para os números? Mas lembre-se de que podemos voltar
a utilizá-las sempre para melhorar o entendimento.

18. 2) Convido-te agora a tentar resolver as seguintes subtrações:
(Use e abuse da técnica do cancelamento para facilitar!)
a) (+7) – (– 4) = b) (– 3) – (– 8) = c) (+4) – (– 11) =
d) (– 5) – (– 5) = e) (+2) – (+ 4) = f) (–2) – (– 3) =
g) 7 – (– 5) = h) – 6 – (–10) = i) +3 – (+ 9) =
j) (– 10) – (+21) = k) (+1) – (– 9) = l) (+3) – (–10) =
m) (– 7) – (– 8) = n) (+12) – (– 12) = o) (–32) – (– 23) =
p) (+27) – (–98) = q) (– 735) – (+426) = r) (– 17) – (– 92) =
s) (+71) – (– 16) = t) (–54) – (– 41) = u) – 74 – ( +58) =
Daremos continuidade às demais operações. Se gostou continue nos
Seguindo.

19. • Convido-te agora a dar prosseguimento aos estudos desse assunto e
passar às operações de multiplicação e divisão de números inteiros.
Bons estudos!
• Obs.: Em caso de dúvida procure pela apresentação: “Operações com
números inteiros positivos e negativos: multiplicação e divisão -
Professor Adriano Augusto – Rede Municipal de Ensino de Belo
Horizonte MG”.