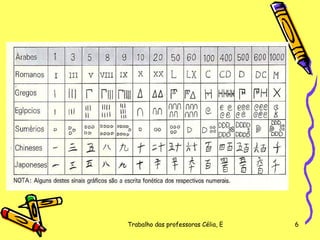
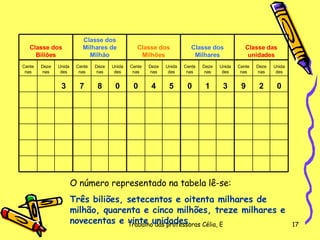
O documento explica a origem dos algarismos numerais de 0 a 9 e como o sistema numeral indo-arábico se desenvolveu e espalhou pelo mundo. O sistema foi criado na Índia no século VI e introduzido na Europa apenas no século XVI depois de ser divulgado pelos árabes, daí o nome "indo-arábico". O sistema representa números usando 10 símbolos e permite cálculos rápidos e precisos.

1. Números Inteiros

3. Por que é que os símbolos 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 se chamam algarismos? Porque derivam do nome do matemático al-Khowarizmi, que originou o termo latino algorismus .

4. Um pouco de história…

5. Muitas civilizações surgidas ao longo da Humanidade criaram ou desenvolveram sistemas de numeração próprios. Os registos dos símbolos usados nesses sistemas constituem o inicio da história da Matemática Eis alguns exemplos de numeração de outros tempos…

7. E chegámos aos nossos dias… No século VI, alguns centros de cultura grega foram fundados na Síria. Ao participar de uma conferência num desses clubes, em 662, o bispo local Severus Sebokt, irritado com o facto de as pessoas elogiarem qualquer coisa vinda dos gregos, explodiu: “ Existem outros povos que também sabem alguma coisa! Os hindus, por exemplo, têm valiosos métodos de cálculo. São métodos fantásticos! E imaginem que os cálculos são feitos por apenas 9 sinais!”

8. A referência a 9 símbolos significa que, na Índia, havia sido inventado no século VI, também, um símbolo para a posição vazio: o zero , que era representado na forma de um ovo de ganso. Pronto, estava completo o sistema de numeração dos algarismos “indo-arábicos”.

9. Ao traduzir livros de matemática indianos para a língua árabe, al-Khowarizmi surpreendeu-se com estranhos símbolos, como o do ovo de ganso. Ao ver que, com aquele sistema de numeração, todos os cálculos seriam feitos de um modo mais rápido e seguro, decidiu contar ao mundo as boas novas, no livro Sobre a Arte Hindu de Calcular . Números Inteiros

10. Por ter sido criado pelos hindus e divulgado pelos árabes é que o sistema é chamado de “indo-arábico” Apesar de completo, só no século XVI seria aceite na Europa.

11. O sistema de numeração árabe ou decimal, (ou de base 10), é o mais utilizado nos dias de hoje. Para representar todos os números, emprega apenas 10 símbolos diferentes, os chamados algarismos árabes. Estes símbolos são: 1, 2, 3, 4, 5, 6, 7, 8, 9 e zero (ou cifra - 0).

13. O símbolo correspondente a um número qualquer compõe-se de vários algarismos dispostos, uns a seguir aos outros, correspondendo, os seus lugares, às diferentes ordens, a começar pela direita.

14. Estes lugares denominam-se por casas: casa das unidades, casa das dezenas, ...

15. Cada algarismo é, também, valorizado segundo a casa que ocupa, indicando a ordem dessas unidades , segundo a casa em que está situado.

16. No quadro seguinte estão indicadas as várias casas, as classes e os grupos, segundo a nomenclatura correspondente ao Sistema de Numeração Árabe (ou decimal):

17. O número representado na tabela lê-se: Três biliões, setecentos e oitenta milhares de milhão, quarenta e cinco milhões, treze milhares e novecentas e vinte unidades. 0 2 9 3 1 0 5 4 0 0 8 7 3 Unidades Dezenas Centenas Unidades Dezenas Centenas Unidades Dezenas Centenas Unidades Dezenas Centenas Unidades Dezenas Centenas Classe das unidades Classe dos Milhares Classe dos Milhões Classe dos Milhares de Milhão Classe dos Biliões

18. Completa a tabela com os seguintes números: 463 055 289 32 392 391 456 2 000 569 127 200 325 000 80 339

19. quinhentos e quarenta e sete mil, novecentos e vinte três unidades 903040037 Três milhões, cinco mil e oito unidades 70003000 Representação fonética Representação gráfica

20. E para terminar não se esqueçam de praticar… Fim