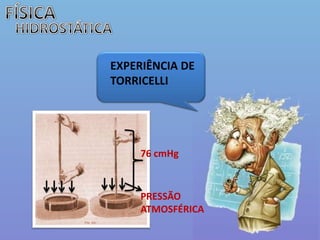
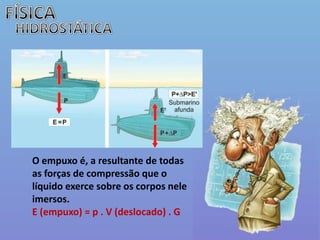
O documento descreve conceitos básicos de hidrostática, incluindo: 1) Hidrostática estuda líquidos e gases em equilíbrio estático; 2) Pressão e densidade são grandezas fundamentais para o estudo; 3) São apresentadas definições, unidades e exemplos de pressão e densidade.

1. FÍSICA HIDROSTÁTICA WGG

2. FÍSICA HIDROSTÁTICA PRIMEIRAMENTE, É NECESSÁRIO SABERMOS QUE, HIDROSTÁTICA É UM RAMO DA MECÂNICA DOS FLUIDOS QUE ESTUDA OS LÍQUIDOS E OS GASES EM EQUILÍBRIO ESTÁTICO.

3. FÍSICA HIDROSTÁTICA PARA DESENVOLVER ESSE ESTUDO, É FUNDAMENTAL O CONHECIMENTO DE DUAS GRANDEZAS FÍSICAS BÁSICAS: PRESSÃO E DENSIDADE ABSOLUTA. E SÃO ELAS QUE VAMOS ESTUDAR A SEGUIR...

4. FÍSICA HIDROSTÁTICA CONCEITOS SOBRE PRESSÃO -CONCEITO DE PRESSÃO PARA WIKIPÉDIA: “A pressão ou tensão mecânica (símbolo: p) é a força normal (perpendicular à área) exercida por unidade de área.” -PARA OS TEÓLOGOS: “Pressão é o grau de penetrabilidade de um objeto em uma superfície.” -PARA OS FUNKEIROS “ A menina quer pressão então” Não foge muito do conceito a cima, mas com outros sentidos...

5. FÍSICA HIDROSTÁTICA Fisicamente, pressão representa a distribuição de uma força normal sobre uma superfície através de uma área do contato com essa superfície. O ELEFANTE ESTÁ FAZENDO UMA PRESSÃO SOBRE A ÁREA EM QUE SE ENCONTRA P= F(n) _ A (m²)

6. FÍSICA HIDROSTÁTICA Um exemplo básico é quando você afia a lâmina de uma faca. Seu objetivo é diminuir a área da faca para que, esta penetre com maior força. Logo pressão e área são grandezas inversamente proporcionais P= F(n) _ A (m²)

7. FÍSICA HIDROSTÁTICA UNIDADES DE MEDIDA A unidade que mede-se pressão é N/m², que pode ser chamado também de Pa(Pascal). 1 atm  1,01 x 10 ou 1 x 10 1 atm  760 cmHg 76 cmHg  1 Pa 5 5

8. FÍSICA HIDROSTÁTICA EXERCÍCIO RESOLVIDO Imagine que uma bailarina, cujo peso é de 480 N, apóia na ponta de um de seus pés, de modo que a área de contato com o solo seja 2,0 cm². Determine a pressão exercida pela bailarina no solo P= F/A  P= 480 N/ 2 cm² P= 240 N/cm² ( NÃO ESTA NO SI) Explique o que ocorrerá com a pressão se ela apoiar-se sobre as pontas de ambos os pés A área de contato com o solo irá aumentar para 4 cm², logo a pressão diminuirá.

9. FÍSICA HIDROSTÁTICA EXERCÍCIO RESOLVIDO Um pingüim muito inteligente estava em um bloco de gelo brincando. Seu desejo era chegar do outro lado do rio desgelado, com apenas alguns blocos de gelo. Mas quando percebeu, seu bloco partiu ao meio, e se ele não tomasse alguma providencia iria afundar. Como ele é provido de inteligência, deitou-se no bloco de gelo, o que o possibilitou de atravessar o rio. Explique por que isso foi possível. Quando ele está de pé, a área de contato dele com o bloco era pequena, o que gera um aumento de pressão. Quando ele deitou, sua área aumentou, diminuindo a pressão.

10. FÍSICA HIDROSTÁTICA A densidade absoluta de um corpo é a razão entre sua massa e seu volume. _ D= M(kg) V (cm³) Normalmente é muito usado g/cm³, porém o correto é kg/m³. Por isso vale lembrar que 1 g/cm³ 10³ kg/m³

11. FÍSICA HIDROSTÁTICA Normalmente, densidade pode vir escrita com a letra grega rô (p) DENSIDADES IMPORTANTES Gasolina: 0,70 g/cm³ Gelo: 0,92 g/cm³ Água: 1 g/cm³ Água do mar: 1,3 g/cm³ Mercúrio: 13,6 g/cm³

12. FÍSICA HIDROSTÁTICA Normalmente, densidade pode vir escrita com a letra grega rô (p) DENSIDADES IMPORTANTES Gasolina: 0,70 g/cm³ Gelo: 0,92 g/cm³ Água: 1 g/cm³ Água do mar: 1,3 g/cm³ Mercúrio: 13,6 g/cm³

13. FÍSICA HIDROSTÁTICA PRESSÃO ATMOSFÉRICA Vivemos mergulhados em um intensa massa de ar,que é nossa atmosfera, constituída de gases como o O2. Essa massa de ar tem uma altura de aproximadamente 50 km. Quanto mais alto, mais rarefeito, ou seja, menos atmosfera.

14. FÍSICA HIDROSTÁTICA EXPERIÊNCIA DE TORRICELLI 76 cmHg PRESSÃO ATMOSFÉRICA

15. FÍSICA HIDROSTÁTICA EXPERIÊNCIA DE TORRICELLI Ao fazer esse experimento, observou-se que a coluna de mercúrio (Hg), em seu interior desceu até atingir uma altura igual a 76 cmHg ficando estática. Assim, conclui-se que era a pressão atmosférica externa sobre o líquido a responsável pelo equilíbrio da coluna de Hg, ou seja, a pressão exercida pela coluna de Hg era igual à exercida pela atmosférica. 1 atm  76 cmHg

16. FÍSICA HIDROSTÁTICA EXERCÍCIO RESOLVIDO Um estudante, ao realizar a experiência de Torricelli em sua cidade, observou que a coluna de Hg atingiu o equilíbrio quando apresentou um altura de 68 cmHg. O que se pode dizer sobre esse experimento? Houve erro em sua realização? Não pode se dizer que foi errado, mas a altitude do local do experimento é inferior a de 1 atm. A cidade deve ser 800 m a nivel do mar, isso porque a cada 100m diminuísse 1cmHg.

17. FÍSICA HIDROSTÁTICA QUEREMOS CALCULAR A PRESSÃO NA BOLINHA. PARA ISSO É NECESSÁRIO SABERMOS: GRAVIDADE É 10 m/s² VAMOS LÁ: Pbolinha= Patmosférica + Pliquido Pb= Pa + FL/ A  Pa + PL/ A Pb= Pa + m.g/ A  Pa + dL. V.g/ A Pb= Pa + dL . A. H.g/ A Pb= Pa + dL . H . g PRESSÃO ATMOSFÉRICA ALTURA P= Pa + dL . H . g

18. FÍSICA HIDROSTÁTICA Essas equações apresentadas anteriormente, são para calcular a pressão em qualquer ponto de um líquido, mudando sempre a altura referente a ele. Claro que você pode só usar a equação final não precisa de tudo aquilo.

19. FÍSICA HIDROSTÁTICA É bom saber também que, se altura em qualquer ponto do liquido for a mesma, a pressão também será a mesma. E = = > > A B C D E D A C B

20. FÍSICA HIDROSTÁTICA É bom saber também que, se altura em qualquer ponto do liquido for a mesma, a pressão também será a mesma. E = = > > A B C D E D A C B

21. FÍSICA HIDROSTÁTICA ENGRAÇADO MAIS É VERDADE EMBORA NÃO PARECE A PRESSÃO NOS TRÊS PONTOS É IGUAL POIS A PRESSÃO ATMOSFÉRICA E pgh É A MESMA A B C

22. FÍSICA HIDROSTÁTICA É BOM SABER.. A PRESSÃO NO GÁS É IGUAL A ATMOSFÉRICA MAIS O DESNÍVEL DE MERCÚRIO POR EXEMPLO 140 cm PG= PA + (130) PG= 76 + 130 PG= 206 LEMBRANDO QUE 1 atm 76 cmHg 10 cm

23. FÍSICA HIDROSTÁTICA EXERCÍCIO RESOLVIDO Lembrando-se que a pressão exercida por um liquido é igual ao produto pgh, qual seria o comprimento da coluna de liquido se a experiência de Torricelli fosse feita com água no lugar de mercúrio. (DENSIDADE DO HG 13,6 g/cm² / DENSIDADE DA ÁGUA 1 g/cm²) Phidrostática = pgH Ph = págua . g. H pmercúrio . g. h’ = págua . g. H H= pmercúrio. H’ / págua H= 13,6. 76 / 1  H = 1034 cm

24. FÍSICA HIDROSTÁTICA EXERCÍCIO RESOLVIDO Qual a pressão em N/m² no fundo de um lago com 10 m de profundidade? Considere: Patm=10 N/m² Densidade da água = 10³ kg/m³ Gravidade= 10 m/s² P= Pa + dgh P= 10 + 10³ . 10 . 10 P= 10 + 10 P= 2 x 10 N/m² 5 5 5 5

25. FÍSICA HIDROSTÁTICA VASOS COMUNICANTES- SE O RECIPIENTE CONTEM O MESMO LÍQUIDO, SÃO IGUAL AS COLUNAS DE LÍQUIDOS NOS DIFERENTES TIPOS DE VASOS. CASO OS LÍQUIDOS NÃO SEJAM O MESMO, AS ALTURAS SERÃO DIFERENTES A B C D = = = A B C D

26. FÍSICA HIDROSTÁTICA EXERCÍCIO RESOLVIDO Dois líquidos estão em equilíbrio num tubo em U conforme a imagem. Sabendo que o liquido A tem densidade de 1,0 g/cm³ , qual a densidade do liquido B P1= P2 Pa + d. g. h = Pa + d’. G. h’ 10³ . 0,05 = d’ . 0,10 50= d. 0,10 d= 500 kg/m³

27. FÍSICA HIDROSTÁTICA PRINCÍPIO DE PASCAL- Se um ponto qualquer de um líquido em equilíbrio sofrer uma variação de pressão, todos os pontos desse líquido sofrerão a mesma variação.

28. FÍSICA HIDROSTÁTICA PRINCÍPIO DE PASCAL F1/A1 = f2/a2

29. FÍSICA HIDROSTÁTICA PRINCÍPIO DE ARQUIMEDES- Todo corpo imerso num fluido, total ou parcialmente, recebe desse uma força de empuxo vertical para cima, igual ao peso do fluido deslocado.

30. FÍSICA HIDROSTÁTICA Um corpo quando mergulhado em um líquido, torna-se aparentemente mais leve. Essa perda aparente de peso deve-se ao fato de que todo liquido exerce sobre os corpos nele imersos uma força resultante.

31. FÍSICA HIDROSTÁTICA O empuxo é, a resultante de todas as forças de compressão que o líquido exerce sobre os corpos nele imersos. E (empuxo) = p . V (deslocado) . G