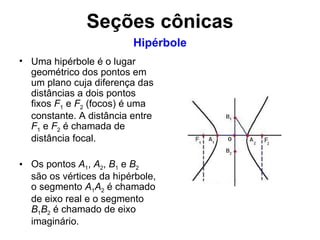
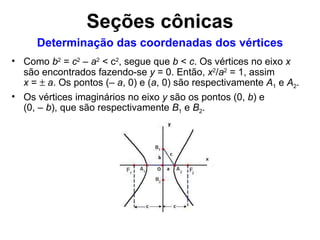
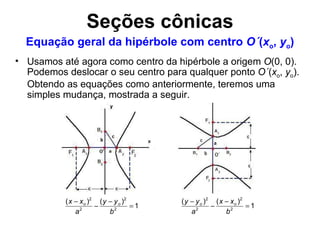
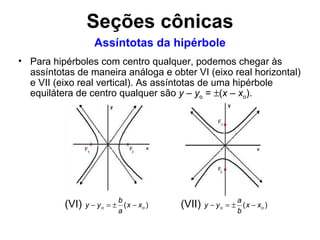
O documento descreve as propriedades geométricas e algébricas da hipérbole, incluindo sua definição como o lugar geométrico dos pontos cuja diferença das distâncias a dois focos é constante. Detalha como obter a equação da hipérbole colocando os focos no eixo x e determinar as coordenadas dos vértices e assíntotas. Apresenta exemplos resolvidos de encontrar focos, vértices e assíntotas dadas equações de hipérboles.

1. Seções cônicas: hipérbole

2. Uma hipérbole é o lugar geométrico dos pontos em um plano cuja diferença das distâncias a dois pontos fixos F 1 e F 2 (focos) é uma constante. A distância entre F 1 e F 2 é chamada de distância focal. Os pontos A 1 , A 2 , B 1 e B 2 são os vértices da hipérbole, o segmento A 1 A 2 é chamado de eixo real e o segmento B 1 B 2 é chamado de eixo imaginário. Hipérbole Seções cônicas

3. Podemos facilitar a obtenção da equação de uma hipérbole colocando seus focos no eixo x, de modo que a origem O (0, 0) fique na metade do caminho entre os focos. Estabelecendo os focos como F 1 (– c , 0) e F 2 ( c , 0) e chamando de 2 a a diferença das distâncias de um ponto genérico P ( x , y ) da hipérbole aos focos, obtemos a equação demonstrada ao lado. Equação da hipérbole no plano cartesiano Seções cônicas

4. Podemos facilitar a obtenção da equação de uma hipérbole colocando seus focos no eixo x, de modo que a origem O (0, 0) fique na metade do caminho entre os focos. Estabelecendo os focos como F 1 (– c , 0) e F 2 ( c , 0) e chamando de 2 a a diferença das distâncias de um ponto genérico P ( x , y ) da hipérbole aos focos, obtemos a equação demonstrada ao lado. Equação da hipérbole no plano cartesiano Seções cônicas

5. Como b 2 = c 2 – a 2 < c 2 , segue que b < c . Os vértices no eixo x são encontrados fazendo-se y = 0. Então, x 2 / a 2 = 1, assim x =  a . Os pontos (– a , 0) e ( a , 0) são respectivamente A 1 e A 2 . Os vértices imaginários no eixo y são os pontos (0, b ) e (0, – b ), que são respectivamente B 1 e B 2 . Determinação das coordenadas dos vértices Seções cônicas

6. Se transferirmos o eixo real de uma hipérbole para o eixo y , obteremos resultados análogos. Observe que todos os pontos notáveis da hipérbole trocam de lugar, passando a ser F 1 (0, c ), F 2 (0, – c ), A 1 (0, a ), A 2 (0, – a ), B 1 (– b , 0) e B 2 ( b , 0). Chamando de 2 a a diferença das distâncias de um ponto genérico P ( x , y ) da hipérbole aos focos, obtemos a equação ao lado (a demonstração é análoga ao caso anterior). Invertendo o eixo Seções cônicas

7. Usamos até agora como centro da hipérbole a origem O (0, 0). Podemos deslocar o seu centro para qualquer ponto O´ ( x o , y o ). Obtendo as equações como anteriormente, teremos uma simples mudança, mostrada a seguir. Equação geral da hipérbole com centro O´ ( x o , y o ) Seções cônicas

8. Isolando o y na equação da hipérbole com eixo real sobre o eixo x e com centro na origem, obtemos as retas mostradas em I. Como a é um valor fixo, vemos que, conforme x vai ficando muito grande, os valores de x 2 – a 2 vão se aproximando de x 2 porque a 2 vai se tornando desprezível. Podemos concluir que y sempre se aproximará das retas II e III, mas nunca as tocará. As retas II e III são as assíntotas da hipérbole. Assíntotas da hipérbole Seções cônicas

9. Quando o eixo real está sobre o eixo y e o centro na origem, as retas IV e V são as assíntotas da hipérbole. Um caso especial é o de hipérbole equilátera: quando o centro está na origem, a é igual a b e suas assíntotas são y =  x . Assíntotas da hipérbole Seções cônicas

10. Para hipérboles com centro qualquer, podemos chegar às assíntotas de maneira análoga e obter VI (eixo real horizontal) e VII (eixo real vertical). A s assíntotas de uma hipérbole equilátera de centro qualquer são y – y o =  ( x – x o ). Assíntotas da hipérbole Seções cônicas

11. 1. Encontre os focos e as assíntotas da hipérbole x 2 /16 – y 2 /9 = 1. Resolução : a = 4 e b = 3. O centro da hipérbole está na origem e seu eixo real sobre o eixo x , então suas assíntotas são y =  3 x /4 . Como c 2 = a 2 + b 2 , então c = 5 . Os focos são (– 5, 0) e (5, 0). 2. Encontre os focos e a equação da hipérbole com vértices (0, 1) e (0, –1) e assíntota y = 2 x . Resolução : O centro da elipse está na origem e seu eixo real sobre o eixo y , então a sua equação é da forma y 2 / a 2 – x 2 / b 2 = 1. Temos que a = 1 e b = 1/2. Como c 2 = a 2 + b 2 , então c = √ 5/2. Os focos são (0, √ 5/2) e (0, – √ 5/2) e a equação é y 2 – 4 x 2 = 1 . Exercícios resolvidos Seções cônicas

12. 1. Encontre os vértices, os focos e as assíntotas da hipérbole 2 y 2 – 3 x 2 – 4 y + 12 x + 8 = 0. 2. Esboce o gráfico de y 2 – x 2 = 4. 3. (Fuvest-SP) A equação de uma das assíntotas da hipérbole de equação x 2 /16 – y 2 /64 = 1 é: a) y = 2 x – 1 b) y = 4 x c) y = x d) y = 2 x + 1 e) y = 2 x 4. (Fuvest-SP) Determine as equações das retas do plano que passam pela origem do sistema de coordenadas e que não intersectam a curva do plano dada pela equação x 2 /4 – y 2 /9 = 1. Exercícios propostos Seções cônicas