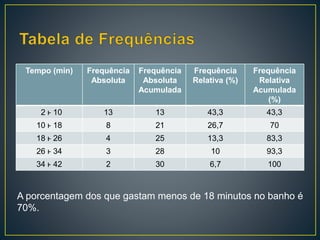
1) O documento apresenta os conceitos de tabela de frequências, média aritmética, média ponderada e medidas de tendência central como mediana e moda. 2) Exemplos ilustram o cálculo da média aritmética, média ponderada, mediana e moda a partir de conjuntos de dados reais. 3) As medidas de tendência central descrevem como os dados se agrupam em torno de determinados valores dentro de uma distribuição.

1. Parte II

2. Os tempos (em minutos) que 30 pessoas gastam no banho são:
• Para construir uma tabela de frequências, devemos agrupar
os valores em um número (escolhido) de intervalos (ou
classes).
• Como o maior valor coletado é 38 e o menor é 2, calcula-se a
diferença entre eles e obtém-se a amplitude total de 36
minutos.
• Podemos dividir a amplitude total por 5, por exemplo. O
quociente é a amplitude do intervalo (ou da classe).
• Assim, 36 : 5 = 7,2 e para facilitar, utilizaremos amplitude de 8
minutos.
3
0
2
0
1
4
5 1
0
1
2
1
6
6 3 2 8 8 8 5 1
0
3
8
3
5
2
8
2
5
5 7 1
4
2
5
2
3
4 3
2
5 9 1
2
1
4

3. Tempo (min) Frequência
Absoluta
Frequência
Absoluta
Acumulada
Frequência
Relativa (%)
Frequência
Relativa
Acumulada
(%)
2 ⱶ 10 13 13 43,3 43,3
10 ⱶ 18 8 21 26,7 70
18 ⱶ 26 4 25 13,3 83,3
26 ⱶ 34 3 28 10 93,3
34 ⱶ 42 2 30 6,7 100
A porcentagem dos que gastam menos de 18 minutos no banho é
70%.

4. • São medidas que descrevem a tendência que os dados
tem de agrupamento em torno de certos valores.
• MÉDIA ARITMÉTICA: é o quociente entre a soma dos
valores observados e o número de observações.
n
x
n
xxx
x
i
n
in 121 ... 





5. Os valores a seguir referem-se às notas obtidas por um
aluno em oito disciplinas de um exame vestibular:
7,5 – 6,0 – 4,2 – 3,9 – 4,8 – 6,2 – 8,0 – 5,4
Calcular a média aritmética desse aluno.
75,5
8
4,50,82,68,49,32,40,65,7
8
8
1






i
i
x
x

6. • Média Aritmética Ponderada: é a média aritmética
calculada com o uso de pesos. Peso é o número de
vezes que o valor se repete.
Sendo xi os valores da variável e pi os respectivos pesos.
i
n
i
ii
n
i
n
nn
p
xp
ppp
xpxpxp
x
1
1
21
2211
...
...









7. As notas de João nos três trimestres do ano letivo em
Matemática foram 6,2; 8,0 e 7,0. Sabendo que o primeiro
trimestre tem peso 1, o segundo peso 2 e o terceiro peso
3, calcule sua média anual.
2,7
6
2,43
321
73822,61
3
1
3
1









i
ii
i
xp
x

8. • MEDIANA: é o valor que divide um grupo de valores previamente
ordenados de modo crescente ou decrescente em duas partes com
o mesmo número de termos. Ou seja, é o termo central do rol. É
representada por Me.
Sejam x1 ≤ x2 ≤ ... ≤ xn os n valores ordenados de uma variável x.
Isto é, se o rol tem quantidade
a) ímpar de elementos, há um que ocupa a posição central, então esse
é a mediana.
b) par de termos, há dois que ocupam a posição central, então a
mediana é a média aritmética desses dois valores.

























 
parénse
XX
ímparénseX
Me nn
n
,
2
,
1
22
2
1

9. Considere os preços do litro de gasolina coletados em seis
postos de gasolina:
R$ 1,99 R$ 2,08 R$ 2,03 R$ 2,05 R$ 1,98 R$ 1,99
Para determinar a Me, vamos colocar os dados em ordem
crescente.
1,98 1,99 1,99 2,03 2,05 2,08
Logo, Me = (1,99 + 2,03)/2 = 2,01

10. • MODA: é (ou são) o valor (ou valores) que aparece(m)
com maior frequência no conjunto de valores
observados. É representada por Mo.
Os salários de seis pessoas que trabalham em uma
empresa são: R$ 700,00, R$ 800,00, R$ 900,00, R$
1000,00, R$ 1000,00 e R$ 5600,00. Determine o salário
modal, o salário médio e o salário mediano.
Mo = 1000

11. 00,666.1
6
000.10
6
600.51000000.1900800700


x
O salário médio é de R$ 1 666,00.
Me = (900 + 1000)/2 = 950
Observe os resultados obtidos e discuta com seus colegas
qual das medidas de centralidade fornece a melhor análise
do problema.