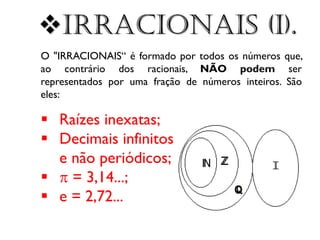
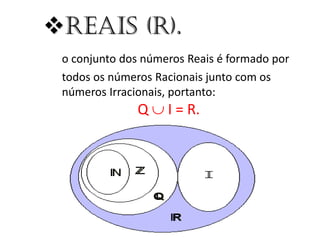
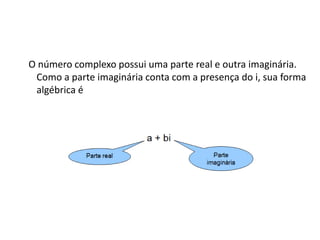
1) O documento discute diferentes conjuntos numéricos, incluindo números naturais, inteiros, racionais, irracionais e complexos. 2) Os números complexos surgiram para resolver equações como x2 + 1 = 0, levando à criação do número i cujo quadrado é igual a -1. 3) Um número complexo possui parte real e imaginária da forma a + bi, onde a é a parte real e b a parte imaginária multiplicada por i.

1. Conjuntos numéricos

2. A história nos mostra que desde muito tempo o
homem sempre teve a preocupação em contar objetos
e ter registros numéricos. Seja através de pedras, ossos,
desenhos, dos dedos ou outra forma qualquer, em que
procurava abstrair a natureza por meio de processos de
determinação de quantidades.
E essa procura pela abstração da natureza foi
fundamental para a evolução, não só, mas também, dos
conjuntos numéricos

3. Naturais (N)
N = {0,1,2,3,4,...}
Problemas do conjunto:
- Subtração: 3 – 4 = ?
- Divisão: 1 : 2 = ?
Como o zero originou-se depois dos outros números e
possui algumas propriedades próprias, algumas vezes
teremos a necessidade de representar o conjunto dos
números naturais sem incluir o zero. Para isso foi definido
que o símbolo * (asterisco) empregado ao lado do símbolo
do conjunto, iria representar a ausência do zero.Veja o
exemplo abaixo:

4. Inteiros (Z)
Z = {...,-2,-1,0,1,2,...}
Problema no conjunto:
Divisão: 1 : 2 = ?
Assim como no conjunto dos naturais, podemos representar
todos os inteiros sem o ZERO com a mesma notação usada
para os NATURAIS.
Inteiros não negativos sem o zero
Inteiros não positivos sem o zero

5. Racionais (Q).
Q = {a/b | a, b  Z e b  0}.
Todo número que pode ser escrito em forma de
fração.
Exemplos:
- Decimais finitos;
- Dízimas periódicas;
- Raízes exatas;
Problema no Conjunto:
Como escrever  em forma de fração?

6. 3,14159265...
Este não é um número Racional, pois possui infinitos
algarismos após a vírgula (representados pelas
reticências)
2,252
Este é um número Racional, pois possui finitos
algarismos após a vírgula.
2,252525...
Este número possui infinitos números após a vírgula,
mas é racional, é chamado de dízima periódica.
Reconhecemos um número destes quando, após a
vírgula, ele sempre repetir um número (no caso 25).
= {Todos os racionais sem o zero}
= {Todos os racionais NÃO NEGATIVOS}
= {Todos os racionais NÃO NEGATIVOS sem o zero, ou seja, os positivos}
= {Todos os racionais NÃO POSITIVOS}
= {Todos os racionais NÃO POSITIVOS sem o zero, ou seja, os negativos}

7. Irracionais (I).
O "IRRACIONAIS“ é formado por todos os números que,
ao contrário dos racionais, NÃO podem ser
representados por uma fração de números inteiros. São
eles:
 Raízes inexatas;
 Decimais infinitos
e não periódicos;
  = 3,14...;
 e = 2,72...

8. Reais (R).
o conjunto dos números Reais é formado por
todos os números Racionais junto com os
números Irracionais, portanto:
Q  I = R.

9. Números Complexos
R
Os números complexos surgiram para sanar
uma das maiores dúvidas que
atormentavam os matemáticos: Qual o
resultado da operação X² + 1 = 0 ?
X² = -1  X =± −1
C

10. Por isso, foi criado um número especial, que
denominamos algebricamente como i, que
elevado ao quadrado resulte em -1,
matematicamente:
I² = -1 i = −1
Esse novo conceito possibilitou a resolução da
equação mostrada anteriormente

11. Desse modo:
X² + 1 = 0
X = ± −1
(como i = ± −1)
X = ±i
Assim, foi criado um novo conjunto numérico
denominado conjunto dos números complexos ou
conjunto dos números imaginários, que
representamos pela letra C.
Conjunto dos números complexos = C

12. O conjunto dos números complexos possui, desse modo, a relação
fundamental onde:
I² = -1
Ou i = √-1

13. O número complexo possui uma parte real e outra imaginária.
Como a parte imaginária conta com a presença do i, sua forma
algébrica é

14. Um número complexo que não possui parte real
(a = 0) é denominado número complexo puro. Um
número complexo que não possua a parte
imaginária (b = 0) é denominado número real e os
números imaginários que possui ambas as partes
são simplesmente chamados de números
complexos.

15. Exemplos
2 + 4i → número complexo
8 - i√2 → número complexo
6i → número complexo puro
4 → número real
-i → número complexo puro
i² → número real