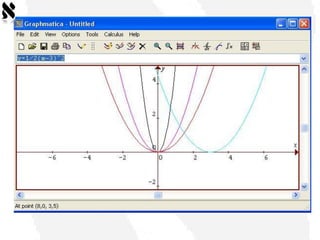
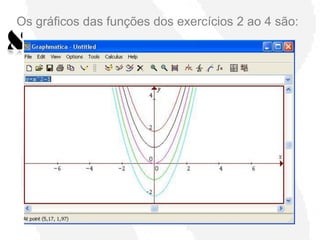
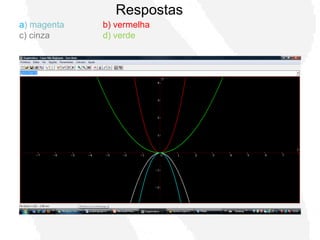
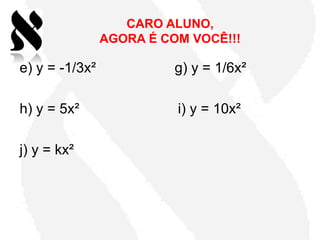
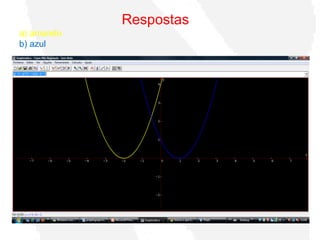
Este documento propõe uma atividade para auxiliar alunos do ensino médio a compreenderem gráficos de funções quadráticas utilizando o software Graphmática. A atividade guiará os alunos a reconstruírem gráficos de funções através de translações, compressões, alongamentos e reflexões da função-mãe y=x2, desenvolvendo entendimento sobre como as equações se relacionam aos gráficos. Uma lista de exercícios irá pedir aos alunos que comparem gráficos de funções modificadas

1. Objetivo
Aula 5 – Apresentação do Graphmática
‫ א‬Desenvolver uma proposta de aula utilizando
alguns recursos do software graphmática (na
verdade o utilizaremos apenas para a
construção e comparação de gráficos), que
possa ser adotada por qualquer professor de
matemática que tenha a sua disposição um
laboratório de informática.

2. ‫ א‬A ideia é desenvolver uma alternativa para a
construção de gráficos, além daquela que é
usualmente vista nas escolas, onde os alunos
constroem o gráfico a partir de uma tabela com
alguns pares ordenados, uma vez que essa
medida é suscetível ao erro, pois, por exemplo,
o gráfico de y = x³ poderia ser confundido com o
gráfico da reta y = x, se considerarmos apenas
os pares ordenados (0,0), (1,1) e (-1,-1).

3. Para Quem?
‫א‬ Preparamos essa proposta pensando no
primeiro ano do Ensino Médio, sendo ela um
complemento ao estudo de funções. No entanto,
vale ressaltar que nessa aula não seriam
abordados conceitos de funções como relação
entre variáveis, domínio e imagem, sendo esses
conhecimentos prévios para esta aula.

4. A Proposta
‫א‬ Nossa proposta é desenvolver uma
atividade simples para auxiliar os alunos
na compreensão dos gráficos de funções
quadráticas.
‫א‬ Partindo de uma função-mãe (y=x²),
iremos usar translações, compressões,
alongamento e reflexões no gráfico desta
função, chegando assim em qualquer
gráfico de função quadrática.

5. ‫א‬ Trabalharemos apenas com funções
quadráticas, pois acreditamos que com
elas já é possível desenvolver os
conceitos envolvidos na construção das
demais funções.

6. ‫א‬ Para desenvolvermos esta proposta,
usaremos o método de completar
quadrados, o que comumente não é
ensinado nas escolas, que acabam
ensinando apenas o método da Fórmula
de Bhaskara para encontrar as raízes das
funções.
‫א‬ Acreditamos que esse método pode
facilitar a compreensão tanto das funções
quanto de seus gráficos, característica
que a Fórmula de Bhaskara não atinge.

7. Recurso
‫א‬ O recurso será o Graphmática, rico
para visualizar a construção de gráficos,
na medida em que mostra as diferenças
entre os gráficos das funções em relação
ao gráfico da função-mãe, y=x².

8. ‫א‬ No caso dos gráficos que sofrem um
alongamento ou uma compressão, por
exemplo, essas alterações são bastante
visíveis com o recurso do software, o que
pode não ser tão evidente ou ser menos
preciso se feito à mão.
‫ א‬Outra vantagem é a rapidez com que o
gráfico é feito, pois se feito a mão, o
tempo despendido para realizar tal tarefa,
talvez desviasse o foco do objetivo, que é
a comparação dos gráficos.
Obs: a função x² no Graphmática é escrito x^2

10. Exercícios Propostos
1) Reconhecimento do programa
‫א‬ Inicialmente iremos propor aos alunos
um momento de contato com o
programa para que, aqueles que não o
conhecem, possam reconhecer suas
funções básicas, bem como sua
linguagem.

11. 2) Desenhe o gráfico da função y = x².
3) Como você imagina que seria o gráfico
da função y = x² + 1 ?
Desenhe o gráfico e veja se sua
suposição estava correta. Qual foi a
modificação que ocorreu? Tente explicar o
porquê desta alteração.

12. 4) Faça o mesmo para as seguintes
funções, comparando-as com y = x².
a) y = x² + 2
b) y = x² – 2
c) y = x² – 1

13. 5) Como você espera que seja o gráfico da
função y = x² + k, sendo k um número
inteiro qualquer?

14. Os gráficos das funções dos exercícios 2 ao 4 são:

15. 6)
Queremos, agora, entender o que
acontece quando multiplicamos a função y =
x² por uma constante. Para isso, compare o
gráfico das seguintes funções com o gráfico
de y = x² e escreva as modificações
ocorridas em cada um deles.
a) y = -x² b) y = 2x²
c) y = -2x² d) y = 1/3x²

16. Respostas
a) magenta b) vermelha
c) cinza d) verde

17. CARO ALUNO,
AGORA É COM VOCÊ!!!
e) y = -1/3x² g) y = 1/6x²
h) y = 5x² i) y = 10x²
j) y = kx²

18. 7)Reescreva as funções a seguir, completando quadrados.
a) y = x² + 4x + 4
b) y = x² - 2x + 1
c) y = x² + 6x + 9
d) y = x² - 8x + 16

19. Respostas
a) amarelo
b) azul

20. 8) A partir de suas respostas, como você
imagina que serão os gráficos das
funções C e D? Utilize o Graphmática
para verificar suas deduções. Compare,
então, cada um dos itens do exercício
anterior com o gráfico de y = x² e escreva
as modificações ocorridas.

21. Com essa lista de exercícios é
esperado que o aluno utilize o software
graphmática e empiricamente possa
fazer deduções sobre a relação entre os
gráficos e as equações de suas
respectivas funções.