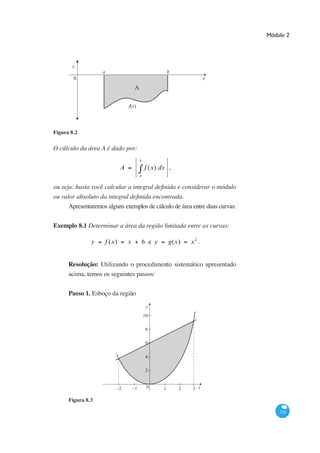
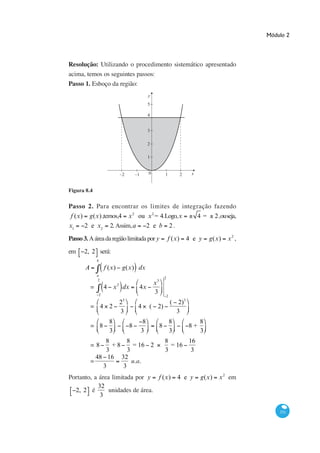
1) O documento apresenta o cálculo da área entre duas curvas através da integral definida. 2) A área é dada pela fórmula A = ∫ab f(x) - g(x) dx, onde f(x) é a curva superior e g(x) a inferior. 3) Dois exemplos ilustram o procedimento passo-a-passo para calcular a área entre diferentes pares de curvas.

1. Módulo 2
Aplicações da Integral
A partir deste momento
Nesta seção vamos abordar uma das aplicações
passaremos a examinar
as aplicações do conteúdo
estudado na Unidade anterior.
matemático – a determinação da área de uma região R do plano, que
estudamos na Unidade 7.
f (x) e g(x) sejam funções con-
a, b e que f (x) g(x) para todo x em
a, b . Então, a área da região limitada acima por y f (x) , abaixo por
y g(x) , à esquerda pela reta x a e à direita pela reta x b , confor-
b
A f (x) g(x) dx .
a
327

2. Curso de Graduação em Administração a Distância
y
f(x)
A
g(x)
[ ]
0 a b x
Figura 8.1
-
de integração. Segue abaixo um procedimento sistemático que podemos
seguir para estabelecer a fórmula, utilizando os seguintes passos.
Passo 1.
acima e qual limita abaixo.
Passo 2. a e b serão
as abscissas x dos dois pontos de interseção das curvas y f (x)
e y g(x) . Para tanto iguala-se f (x) e g(x) , ou seja, faz
f (x) g(x) e resolve-se a equação resultante em relação a x.
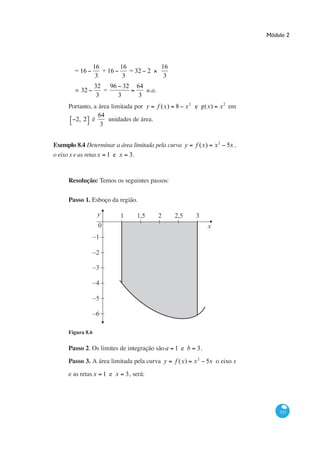
Passo 3.
curvas.
Observação
f (x) , pelas retas x a e x b e o eixo x, onde f (x) é uma
função contínua sendo f (x) 0 , para todo x em a, b , conforme
328

3. Módulo 2
y
a b
0 x
A
f(x)
Figura 8.2
O cálculo da área A é dado por:
b
A f (x) dx ,
a
Apresentaremos alguns exemplos de cálculo de área entre duas curvas:
Exemplo 8.1 Determinar a área da região limitada entre as curvas:
y f (x) x 6 e y g(x) x2 .
Resolução: Utilizando o procedimento sistemático apresentado
acima, temos os seguintes passos:
Passo 1. Esboço da região
y
10
8
6
4
2
−2 −1 0 1 2 3 x
Figura 8.3
329

4. Curso de Graduação em Administração a Distância
Passo 2. Para encontrar os limites de integração ,fazemos
f (x) g(x) , isto é, x 6 x 2 ou x 2 x 6, que fornece
2
x x 6 0
da equação acima, x 2 e x 3 , que serão os limites de inte-
gração. Observe, pelo x 6 x 2 , para todo
x em 2, 3 .
Passo 3. Calculando a área da região limitada por:
y f (x) x 6 e y g(x) x 2 em 2, 3 temos :
b
A f (x) g(x) dx
a
3 3
2
= x 6 x dx x 6 x 2 dx
2 2
3
x2 x3
= 6x
2 3
2
32 33 ( 2)2 ( 2)3
= 6 3 6 ( 2)
2 3 2 3
9 4 8
= + 18 32 12
2 2 3
9 8
= + 18 9 2 12 +
2 3
9 8 9 18 30 8
9 10
2 3 2 3
27 22 27 22 81 + 44 125
= = u.a.
2 3 2 3 6 6
Portanto, a área limitada por
125
y f (x) x 6 e y g(x) x 2 em 2, 3 é
6
unidades de área.
Exemplo 8.2 Determinar a área da região limitada por
y f (x) 4 e y g(x) x2 .
330

5. Módulo 2
Resolução: Utilizando o procedimento sistemático apresentado
acima, temos os seguintes passos:
Passo 1. Esboço da região:
y
5
4
3
2
1
−2 −1 0 1 2 x
Figura 8.4
Passo 2. Para encontrar os limites de integração fazendo
f (x) g(x) ,temos,4 x 2 ou x 2 = 4.Logo,x 4= 2,ouseja,
x1 2 e x2 2. Assim, a 2 e b 2.
Passo 3. A área da região limitada por y f (x) 4 e y g(x) x2 ,
em 2, 2 será:
b
A f (x) g(x) dx
a
2
2
2 x3
= 4 x dx 4x
2
3
2
23 ( 2)3
= 4 2 4 ( 2)
3 3
8 8 8 8
= 8 8 8 8+
3 3 3 3
8 8 8 16
=8 +8 = 16 2 = 16
3 3 3 3
48 16 32
= u.a.
3 3
Portanto, a área limitada por y f (x) 4 e y g(x) x 2 em
32
2, 2 é unidades de área.
3
331

6. Curso de Graduação em Administração a Distância
Exemplo 8.3 Determinar a área da região limitada por
y f (x) 8 x 2 e g(x) x2 .
Resolução: Temos os seguintes passos:
Passo 1. Esboço da região:
y
8
7
6
5
4
3
2
1
−2 −1 0 1 2 x
Figura 8.5
Passo 2. Para encontrar os limites de integração, fazemos
f (x) g(x) , isto é, 8 x 2 x 2 , que fornece 8 2 x2 e
x1 2 e x2 2 . Assim, a 2 e b 2.
Passo 3. A área da região limitada por y f (x) 8 x 2 e g(x) x2
será:
b 2
A f (x) g(x) dx 8 x2 x 2 dx
a 2
2
2
2 x3
= 8 2 x dx 8x 2
2
3
2
3
2 ( 2)3
= 8 2 2 8 ( 2) 2
3 3
8 8
= 16 2 16 2
3 3
332

7. Módulo 2
16 16 16
= 16 + 16 = 32 2
3 3 3
32 96 32 64
= 32 = u.a.
3 3 3
Portanto, a área limitada por y f (x) 8 x 2 e g(x) x 2 em
64
2, 2 é unidades de área.
3
Exemplo 8.4 Determinar a área limitada pela curva y f (x) x2 5x ,
o eixo x e as retas x 1 e x 3.
Resolução: Temos os seguintes passos:
Passo 1. Esboço da região.
y 1 1,5 2 2,5 3
0 x
−1
−2
−3
−4
−5
−6
Figura 8.6
Passo 2. Os limites de integração são a 1 e b 3.
Passo 3. A área limitada pela curva y f (x) x2 5x o eixo x
e as retas x 1 e x 3, será:
333

8. Curso de Graduação em Administração a Distância
3
3
2 x3 x2
A x 5x dx 5
1
3 2
1
33 32 13 12
= 5 5
3 2 3 2
27 9 1 1
= 5 5
3 2 3 2
45 1 5 18 45 2 15
= 9
2 3 2 2 6
27 13 27 13
=
2 6 2 6
81 + 13 68 34 34
= u.a.
6 6 3 3
Portanto, a área limitada pela curva y f (x) x 2 5x , o eixo x
34
e as retas x 1 e x 3 é unidades de área.
3
Exemplo 8.5 Encontrar a área da região limitada pela curva
y f (x) sen x e pelo eixo x de 0 a 2 .
Resolução:
Passo 1. Esboço da região:
y
1
0 x
2 2
1
Figura 8.7
334

9. Módulo 2
Passo 2. Para determinar os limites de integração, temos, pelo
0, , f (x) sen x 0 e no interva-
lo ,2 , f (x) sen x 0.
Passo 3. A área da região limitada pela curva f (x) sen x , e pelo
eixo x de 0 até 2 será:
2
2
A sen x dx sen x dx c os x 0 cos x
0
= cos ( cos 0) + cos 2 ( cos
= ( 1) ( 1) + 1 ( 1)
= 1+1+ 1 1 =2+ 2 = 2 + 2 = 4 u.a.
Portanto, a área da região limitada pela curva f (x) sen x e pelo eixo
x de 0 até 2 é 4 unidades de área.
dúvidas, busque orientação junto ao
Exercícios propostos – 1
y
a)
5
4
3
2
1
0 1 2 3 4 x
Figura 8.8
335

10. Curso de Graduação em Administração a Distância
Onde y f (x) x 1.
b) y
4
3
2
1
0 1 2 3 4 x
Figura 8.9
Onde y f (x) x.
2) Determinar a área da região limitada por:
y f (x) x e y g(x) x2 x.
3) Determinar a área da região limitada por y f (x) x 1, o eixo
x e as retas x 2 e x 0.
4) Determinar a área da região limitada por
2 2
y f (x) x e y g(x) x 4x .
1
5) Calcular a área da região limitada por y f (x) , o eixo x e
x
as retas x 1 e x 4.
Volume de sólido de revolução
-
centro de
massa e de momento de inércia. Como é difícil determinar o volume de
um sólido de forma irregular, começaremos com objetos que apresentam
formas simples. Incluídos nesta categoria estão os sólidos de revolução.
336

11. Módulo 2
Um sólido de revolução é gerado pela rotação de uma região do pla-
eixo de revolução, contida no plano.
Seja S o sólido gerado pela rotação da região do plano limitada
por y f (x) , o eixo x , x a e x b em torno do eixo x . Então o
volume V deste sólido é dado por:
b 2
V f (x) dx.
a
-
tes aos usados para calcular a área de uma região plana e limitada, mas
y
y = f(x)
a 0 b x
Figura 8.10
337

12. Curso de Graduação em Administração a Distância
y
x
Figura 8.11
Analogamente, quando o eixo de revolução é o eixo y e a frontei-
ra da região plana é dada pela curva x g(y) e o eixo y entre y c e
y d , então o volume V do sólido de revolução é dado por
d 2
V g y dy.
c
y
d
x = g(y)
0 x
c
Figura 8.12
338

13. Módulo 2
Sejam f x e g x funções contínuas no intervalo a,b e su -
mos que f x g x 0 para todo x a,b . Então o volume do sólido
de revolução gerado pela rotação em torno do eixo x , da região limitada
pelas curvas y f x e y g x e as retas x a e x b é dado por:
b 2 2
V f x g x dx.
a
y
y = f(x)
y = g(x)
a 0 b x
Figura 8.13
y
x
Figura 8.14
339

14. Curso de Graduação em Administração a Distância
Exemplo 8.6 A região limitada pela curva y x 2 , o eixo x e as retas
x 1 e x 2 , sofrem uma rotação em torno do eixo x . Encontre o
volume do sólido de revolução gerado.
Resolução:
y
y = f(x)
4
1
0 1 2 x
Figura 8.15
Temos:
b 2 2 2
V f x dx x 2 dx
a 1
2
x5
32 1
5 1 5
31
, unidades de volume (u.v.).
5
Exemplo 8.7 Calcule o volume do sólido que se obtém por rotação da
região limitada por y x 3 , y 0 e x 1 em torno do eixo y .
340

15. Módulo 2
Resolução:
y
2 y = x3
1,5
1
0,5
−1 −0,5 0 0,5 1 1,5 2 x
−0,5
−1
Figura 8.16
De y x 3 temos x y1/ 3 . Logo, o volume do sólido obtido pela
revolução em torno do eixo y é dado por
d 2 1
V g y dy y 2/ 3dy
c 0
3 5/ 3 1 3
y u.v.
5 0 5
Exemplo 8.8 Calcule o volume do sólido que se obtém por rotação da
região limitada por x 2 y 2 , 2y x 2 0,x 0 e x 1em torno
do eixo x .
341

16. Curso de Graduação em Administração a Distância
Resolução:
y
5
x² = y−2
4
3
2 2y−x−2 = 0
1
x
−2 0 2 4
−1
Figura 8.17
(a) Volume do sólido em torno do eixo x . Neste caso, temos
b 2 2
V f x g x dx
a
2
1
2
2 1
x 2 x 1 dx
0 2
1 15 2
x4 x x 3 dx
0 4
1
x5 5x 3 x2
3x
5 4 2
0
1 5 1 79
3 u.v.
5 4 2 20
342

17. Módulo 2
Exercícios propostos – 2
1) Determine o volume do sólido de revolução gerado pela rotação em
torno do eixo x , de região limitada por:
a) y 2x 1, x 0, x 3e y 0.
b) y x 2 1, x 1, x 3e y 0.
2) Determine o volume do sólido de revolução gerado pela rotação
em torno do eixo y , de região limitada por: y ln x, y 1, y 3
e x 0.
3) Calcule o volume do sólido obtido girando cada região limitada
pelas curvas e retas dadas em torno do eixo indicado:
a) y 2x 2 , y 0, x 0, x 5 ; em torno do eixo dos x .
b) y x2 5x 6, y 0 ; em torno do eixo dos x .
c) y2 2x , x 0, y 0 ey 3; em torno do eixo dos y .
d) y 2x 1, x 0, x 3 ey 0 ; em torno do eixo dos x .
343

18. Curso de Graduação em Administração a Distância
Comprimento de arco
A seguir, apresentaremos o comprimento de arco de uma curva
plana em coordenadas cartesianas. Seja f uma função contínua no in-
[a,b] y f (x) .
y
B = (b,ƒ(b))
y = ƒ(x)
A = (a,ƒ(a))
a b x
Figura 8.18
Sejam A a, f (a) e B(b, f (b)) dois pontos na curva y f (x) .
ª
Seja s o comprimento da curva AB y f (x) .
Então, s é dado por
b 2
s 1 f '(x) dx.
a
A seguir, apresentaremos alguns exemplos.
x
Exemplo 8.9 Determinar o comprimento de arco da curva y 1,
2
0 x 3.
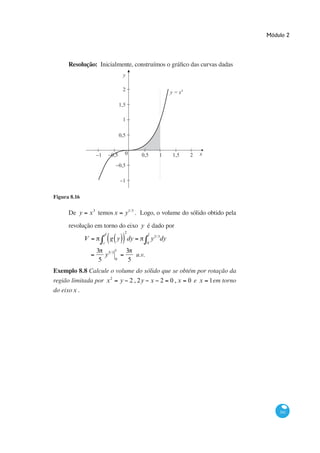
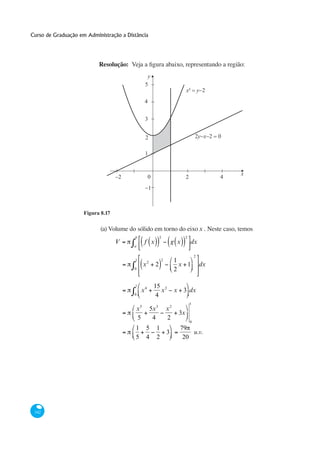
Resolução: Temos,
x 1
y 1 y' .
2 2
344

19. Módulo 2
Logo,
b 2
s 1 f '(x) dx
a
3 1
1 dx
0 4
3 5 3 5 3
dx 5. x
0 4 2 4 0
x
Portanto, o comprimento de f (x) 1, para 0 x 3 é dada
2
3
por s 5 u.c.
2
Exemplo 8.10 Calcule o comprimento do arco da curva 24xy x4 48
de x 2ax 4
Resolução: Temos,
24xy x4 48
1 3 2
y x
24 x
2
3x 2 x 4 16
y' .
24 x 2 8x 2
Agora, 2
b 2 4 x 4 16
s 1 y' dx 1 dx
a 2 8x 2
4 1
1 4
x8 256 32x 4 dx
2 64x
4 x8 32x 4 256
dx
2 64x 4
4 (x 4 16)2 4 (x 4 16)2
dx dx
2 (32x 2 )2 2
(32x 2 )2
4 x 4 16
dx
2 8x 2
4
1 4
2 2 1 x3 16
x 16x dx
8 2 8 3 x
2
1 64 8 1 56 17
4 8 4 u.v.
8 3 3 8 3 6
345

20. Curso de Graduação em Administração a Distância
compreendeu estas importantes
e para isto tente resolver os
exercícios propostos a seguir. Se
las antes de seguir adiante.
Exercícios propostos – 3
Determine o comprimento das curvas dadas por:
x2 1
1) y ln x, 2 x 4.
2 4
1 3
2) y ln 1 x 2 de x ax .
4 4
1 4 1
3) y x de x 1 a x 2.
4 8x 2
4) y 1 ln sen x de x ax .
6 4
1 x
5) y e e x
de x 0 a x 1.
2
Saiba Mais...
Para aprofundar os conteúdos abordados neste capítulo consulte:
FLEMMING, D. M.; GONÇALVES, M. B. Cálculo A: Fun-
ções, Limite, Derivação, Integração, 5ª ed. São Paulo: Makron
Books, 1992.
LEITHOLD, Louis. O cálculo com geometria analítica. 2. ed.
São Paulo: Harbra, 1994. Vol. 1.
346

21. Módulo 2
RESUMO
do sólido de revolução, e no comprimento de arco de uma curva
utilizando o sistema de coordenadas cartesianas.
347

22. Curso de Graduação em Administração a Distância
RESPOSTAS
• Exercícios propostos – 1
16
1) a) 12 unidades de área. b) unidades de área.
3
4
2) unidades de área.
3
3) 4 unidades de área.
8
4) unidades de área.
3
5) 2 unidades de área.
• Exercícios propostos – 2
1016
1) a) 57 u.v.; b) u.v.
15
1
2) e6 u.v.;
2 e2
3) a) 2500 u.v. b) u.v.
30
243
c) u.v. d) 21 u.v.
20
• Exercícios propostos – 3
1
1) 6+ ln 2 6,173u.c.
4
21 1 123
2) ln u.c. 3) u.c.
5 2 32
1
4) ln 2 ln 2 2 ln 2 3 u.c.
2
1 2
5) e 1 u.c.
2e
348