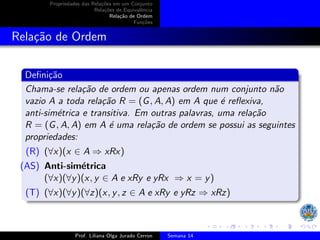
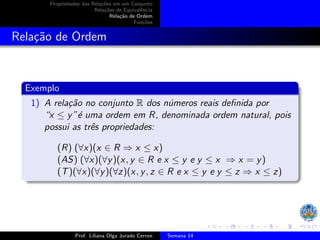
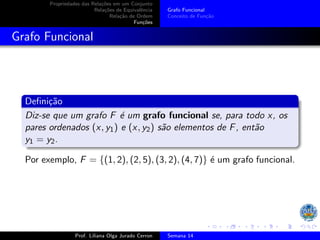
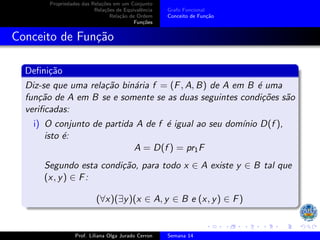
O documento discute as propriedades de relações em conjuntos, incluindo: (1) relações de equivalência, que são reflexivas, simétricas e transitivas; (2) relações de ordem, que são reflexivas, antissimétricas e transitivas; e (3) exemplos de relações que satisfazem essas propriedades, como igualdade e divisibilidade.