O documento discute grafos e suas propriedades. Em três frases ou menos:
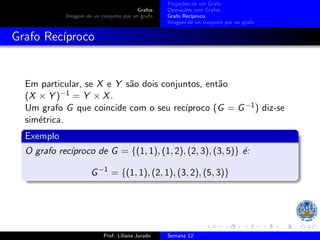
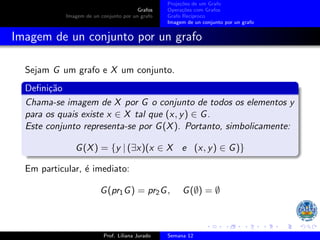
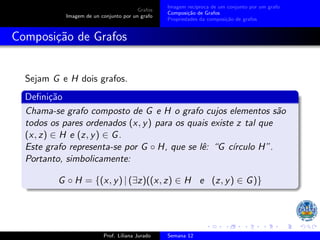
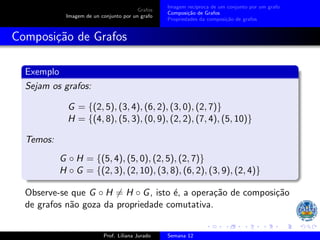
1) Grafos são conjuntos de pares ordenados e exemplos incluem {(a,1), (3,(3,4))} e {(1,2), (2,3), (1,4)}. 2) As projeções de um grafo G são os conjuntos pr1G e pr2G de seus primeiros e segundos elementos. 3) A composição de grafos G e H é o grafo G ◦ H cujos elementos são pares (x,y) tal que existe z com (x,z) em H