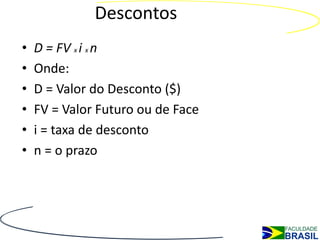
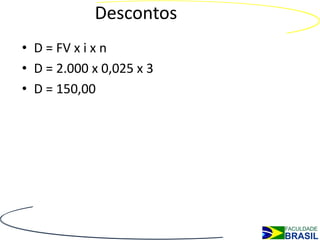
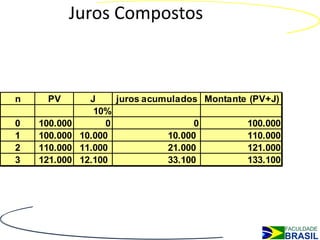
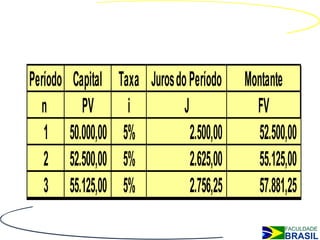
O documento explica os conceitos de descontos e juros compostos. No desconto, o valor presente de um título é calculado a partir do seu valor futuro, usando taxas de desconto. Nos juros compostos, os juros de cada período são incorporados ao capital e geram juros sobre juros, resultando em montantes maiores. Fórmulas para cálculo de descontos, taxas efetivas e montantes em juros compostos são apresentadas.

1. Material de Apoio

2. Descontos
• Conceito: a chamada operação de desconto
normalmente é realizada quando se conhece o
valor futuro de um título (valor nominal, valor de
face ou valor de resgate) e se quer determinar o
seu valor atual.

3. Descontos
• Fórmula: D = FV – PV
• Onde:
• D = valor monetário do desconto
• FV = Valor Futuro (Valor de Face)
• PV = Valor Presente (Valor creditado ou pago ao
seu titular)

4. Descontos
• O critério mais utilizado pelo mercado é o
chamado desconto simples, que envolve cálculos
lineares, com um detalhe: o taxa no período
incide sobre o valor futuro e não sobre o valor
presente (como são as demais operações)

5. Descontos
• Conhecido no mercado financeiro como
desconto bancário ou comercial, o desconto
simples é obtido multiplicando-se o valor de
resgate do título pela taxa de desconto e pelo
prazo a decorrer até o seu vencimento, ou seja:

6. Descontos
• D = FV x i x n
• Onde:
• D = Valor do Desconto ($)
• FV = Valor Futuro ou de Face
• i = taxa de desconto
• n = o prazo

7. Descontos
• Para se obter o chamado valor descontado (ou
valor presente), basta subtrair o valor do
desconto do valor futuro do título, como segue:
• PV = FV - D

8. Descontos
• Assim, temos as duas fórmulas básicas:
• D = FV x i x n
• PV = FV - D

9. Descontos
• Exemplos:
• 1- Qual o valor do desconto simples de um título de $ 2.000,00,
com vencimento para 90 dias, à taxa de 2,5% ao mês?
• Dados:
• FV = 2.000,00
• n = 90 dias = 3 meses
• i = 2,5% ao mês

10. Descontos
• D = FV x i x n
• D = 2.000 x 0,025 x 3
• D = 150,00

11. Descontos
Cálculo do valor do desconto simples para séries
de títulos de mesmo valor:
Fórmulas:
PVt = FV x N - Dt
Dt = FV x N x i x (t1 + t2)/2

12. Descontos
• Onde:
• Dt = valor do desconto total
• N = número de títulos
• i = taxa de juros
• t1 + t2 = prazo médio dos títulos
2

13. Descontos
• Exemplo: Calcular o valor líquido
correspondente ao desconto bancário de 12
títulos, no valor de $ 1.680,00 cada um,
vencíveis de 30 a 360 dias, respectivamente,
sendo a taxa de desconto cobrada pelo banco de
2,5% ao mês.

14. Descontos
• Dados:
• FV = 1.680,00
• N = 12
• t1 = 1
• tn = 12
• Pt = ?
• i = 2,5%

15. Descontos
• Solução:
• Dt = 1.680,00 x 12 x 0,025 x (1 + 12)/2
• Dt = 3.276,00
• Pt = (1.680,00 x 12) – 3.276,00
• Pt = 16.884,00

16. Descontos
• Taxa Efetiva de Desconto (ie)
• É aquela que, como o próprio nome diz, remunera efetivamente
uma operação de desconto.
• Há uma mudança de enfoque, veja:
• A loja de eletrodomésticos, ao permitir que seus clientes paguem
30 dias após a compra, está realidade, abdicando de receber $
900,00, hoje, para receber $ 1.000,00 daqui a um mês. Quanto
ganhará com isso?

17. Descontos
• O rendimento será de $ 100,00 sobre os $
900,00 de hoje. A taxa de remuneração ou taxa
efetiva será:
• Ie = 100/900 x 100 = 11,11%.

18. Descontos
• Assim podemos dizer:
• A taxa nominal de desconto (id) incide sobre o
valor nominal do título. Já a taxa efetiva de
desconto (ie) é aplicada sobre o valor líquido da
operação.

19. Descontos
• ie = id x 100
100 – id
Onde:
ie = taxa efetiva de desconto
id = taxa nominal de desconto

20. Juros Compostos
• No regime de juros compostos, os juros obtidos a cada novo
período são incorporados ao capital, formando um montante que
passará a participar da geração de juros no período seguinte, e
assim sucessivamente. Dessa forma, não apenas o capital inicial
rende juros, mas eles são devidos a cada período de forma
cumulativa. Daí serem chamados juros capitalizados.

21. Juros Compostos
• PV = Capital inicial
• n = Números de períodos
• FV = Montante no regime de juros compostos
• No regime de juros compostos, a taxa de juros (i) incide sobre o
montante (PV+J) do período anterior. Portanto, difere do regime
de juros simples, em que a incidência é sempre sobre o capital
inicial (PV).

22. Juros Compostos
• Exemplo 1: Para um capital de $ 100.000,00,
aplicado à taxa de 10% ao mês, em juros
compostos, por 3 meses, teríamos:

23. Juros Compostos
n PV J juros acumulados Montante (PV+J)
10%
0 100.000 0 0 100.000
1 100.000 10.000 10.000 110.000
2 110.000 11.000 21.000 121.000
3 121.000 12.100 33.100 133.100

24. Juros Compostos
• Observe que os juros são cobrados a cada
período de capitalização que, neste caso, é
mensal. No período n=0, o capital ainda não
rendeu juros, pois é nesse momento que a
aplicação se inicia. A remuneração (juros) de
cada período é obtida pela multiplicação do
montante do período anterior pela taxa de juros.

25. Juros Compostos
• A) Primeiro período:
• Juros: J1 = PV x i
100
J1 = 100.000 x 10/100 = 10.000
Montante: FV1 = PV + PV x i
100
FV1 = PV ( 1 + i )
100
Montante do primeiro período

26. Juros Compostos
• B) Segundo Período
• Juros: J2 = FV1 x i
100
J2 = 110.000 x 10/100 = 11.000
Verifique que o juro aumentou em 1.000, que corresponde à
parcela incidente sobre os juros do período anterior (10.000 x
10/100). Por isso os juros compostos são chamados de juros
sobre juros.

27. Juros Compostos
• Montante: FV2 = FV1 + J2
• FV2 = FV1 + FV1 x i
100
• FV2 = FV1 ( 1 + i )
100
• FV2 = PV ( 1 + i ) x ( 1 + i )
100 100
• FV2 = PV ( 1 + i )2 Montante 2.º período
100

28. Juros Compostos
• C) Terceiro Período:
• Juros: J3 = FV2 x i
100
J3 = 121.000 x 10/100 = 12.100
• Montante: FV3 = FV2 + J3
• FV3 = FV2 + FV2 x i
100
• FV3 = PV ( 1 + i ) 2 x ( 1 + i )
100 100
• FV3 = PV ( 1 + i )3 Montante 3.º período
100

29. Juros Compostos
• Portanto, generalizando a fórmula para “n”
períodos, temos:
• FVn = PV ( 1 + i )n
100
ESTA É A FÓRMULA GERAL DE JUROS
COMPOSTOS.

30. Juros Compostos
• Observação:
• A unidade de tempo utilizada para o período (n)
deve ser a mesma da taxa de juros (i), ou seja, se
o período (n) é dado em:
• Dia – taxa em dia (i% a.d.);
• Mês – taxa em mês (i% a.m.);
• Ano – taxa em ano (i% a.a.)

31. Juros Compostos
• Outro exemplo: Uma aplicação de $ 50.000,00,
pelo prazo de 3 meses, a uma taxa de 5% a.m.
(0,05 a.m.), capitalizável mensalmente, quanto
renderá?
• FVn = PV ( 1 + i )n
100

32. Juros Compostos
• FV = 50.000 ( 1,05 )3
• FV = 57.881,25
• Esse é montante, os juros (rendimentos) são:
• J = MONTANTE – CAPITAL INICIAL
• J = 57.881,25 – 50.000,00
• J = 7.881,25
• Veja o que ocorreu em cada período no quadro a seguir:

33. Juros Compostos
Período Capital Taxa Juros do Período Montante
n PV i J FV
1 50.000,00 5% 2.500,00 52.500,00
2 52.500,00 5% 2.625,00 55.125,00
3 55.125,00 5% 2.756,25 57.881,25