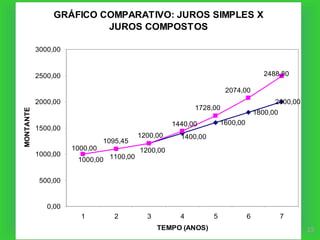
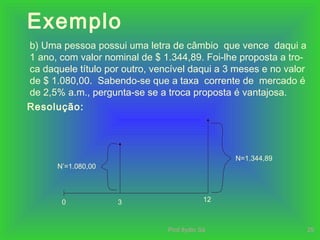
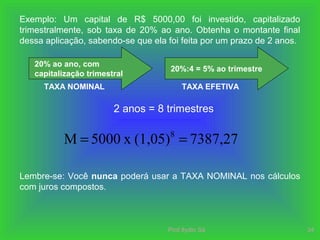
O documento discute os conceitos de juros simples e juros compostos. Apresenta as fórmulas para calcular juros e montantes em cada regime, destacando que os juros compostos geram montantes maiores devido à incorporação dos juros ao capital a cada período.

1. Prof.Ilydio Sá 1
Matemática
Financeira(Juros Simples x Juros Compostos)

2. Prof.Ilydio Sá 2
Taxa de Juros
FORMA PORCENTUALFORMA PORCENTUAL
• Na forma porcentual a taxa de juros é aplicada a centos do
capital.
Ex.: 12% ao ano.
FORMA UNITÁRIAFORMA UNITÁRIA
• Na forma unitária a taxa de juros é aplicada a unidades do
capital.
Ex.: 0,12 ao ano.

3. Prof.Ilydio Sá 3
JUROS SIMPLES

4. Prof.Ilydio Sá 4
CÁLCULO DO JURO
- Ao valor aplicado;
- Ao tempo de aplicação.
- Ao valor aplicado;
- Ao tempo de aplicação.
JURO SIMPLES
• A remuneração pelo capital inicial
(o principal) é diretamente proporcional:

5. Prof.Ilydio Sá 5
CÁLCULO DO JURO
• FÓRMULA BÁSICA:
J = C . i . nJ = C . i . nJ = C . i . nJ = C . i . n
onde:
J = Juro
C = Capital inicial (Principal)
i = Taxa de Juros (na forma unitária)
n = prazo de aplicação (na mesma unidade que a taxa)
EXEMPLO

6. Prof.Ilydio Sá 7
MONTANTE
JURO SIMPLES
• Montante é a soma do juro mais o capital
aplicado.
M = C + J
onde:
C= principal
n= prazo de aplicação
i = taxa de juros
M = C(1 + in) = C. FATOR
EXEMPLO

7. Prof.Ilydio Sá 9
TAXA PROPORCIONAL
JURO SIMPLES
A taxa i1 (referida ao período n1) é proporcional à taxa i2 (referida ao
período n2) se:
2
1
2
1
n
n
i
i
=
Ou, do mesmo modo, se:
Ou ainda:
2
2
1
1
n
i
n
i
=
EXEMPLO
1221 .nin.i =

8. Prof.Ilydio Sá 12
TAXAS EQUIVALENTES
Duas taxas de juros são equivalentes se:
• aplicadas ao mesmo capital;
• pelo mesmo intervalo de tempo.
=> Ambas produzem o mesmo juro.
No regime de juros simples, as taxas de juros
proporcionais são igualmente equivalentes.

9. Prof.Ilydio Sá 13
JURO EXATO
Juro Exato é aquele em que:
• o período a que se refere a taxa está expresso em
dias.
• é adotada a convenção do ano civil.
EXEMPLO

10. Prof.Ilydio Sá 15
JURO COMERCIAL
Juro comercial é aquele em que:
• o período a que se refere a taxa está expresso em dias.
• é adotada a convenção do ano comercial (360 dias):
EXEMPLO

11. Prof.Ilydio Sá 17
JUROS COMPOSTOS

12. Prof.Ilydio Sá 18
Juros Compostos
Juros Simples:
• Apenas o capital inicial rende juros;
• O Juro é diretamente proporcional ao tempo e à taxa.
Juros Compostos:
• O Juro gerado pela aplicação, em um período, será
incorporado;
• No período seguinte, o capital mais o juro passa a ge-
rar novos juros;
• O regime de juros compostos é mais importante, por-
que retrata melhor a nossa realidade.

13. Prof.Ilydio Sá 19
Diferença entre os regimes
de capitalização
Co= 1000,00
i= 20 % a.a.
n= 5 anos
n
Juro por Período Montante Juro por período Montante
0 0 1000,00 0 1000,00
1 1000 x 0,2 = 200 1200,00 1000 x 0,2 = 200 1200,00
2 1000 x 0,2 = 200 1400,00 1200 x 0,2 = 240 1440,00
3 1000 x 0,2 = 200 1600,00 1440 x 0,2 = 288 1728,00
4 1000 x 0,2 = 200 1800,00 1728 x 0,2 = 346 2074,00
5 1000 x 0,2 = 200 2000,00 2074 x 0,2 = 414,80 2488,80
Juros Simples Juros Compostos

14. Prof.Ilydio Sá 20
GRÁFICO COMPARATIVO: JUROS SIMPLES X
JUROS COMPOSTOS
1800,00
2000,002074,00
2488,80
1400,00
1200,001000,00
1600,00
1200,00
1440,00
1000,00
1728,00
0,00
500,00
1000,00
1500,00
2000,00
2500,00
3000,00
1 2 3 4 5 6
TEMPO (ANOS)
MONTANTE

15. Prof.Ilydio Sá 21
Uma questão: Será que, pelo que vimos no
gráfico anterior, podemos então concluir que os
montantes gerados, sob as mesmas condições
e sobre o mesmo capital, a juros simples e a
juros compostos ou são iguais ou o montante
dos juros compostos será maior?
Para ajudar na resposta, vamos incluir na
tabela e no gráfico anterior mais uma linha.
Vamos calcular os dois montantes para um
prazo de 15 dias após o início da aplicação, ou
seja, após meio mês.

16. Prof.Ilydio Sá 22
JUROS SIMPLES JUROS COMPOSTOS
Montante Montante
0 1000,00 1000,00
0,5 1000 x 1,1 = 1100 1000 x 1,2^0,5= 1095,45
1 1000 x 1,2 = 1200 1000 x 1,2 = 1200
2 1000 x 1,4 = 1400 1000 x 1,2^2 = 1440
3 1000 x 1,6 = 1600 1000 x 1,2^3 =1728
4 1000 x 1,8 = 1800 1000 x 1,2^4 =2074
5 1000 x 2,0 = 2000 1000 x 1,2^5 = 2488,8

17. Prof.Ilydio Sá 23
GRÁFICO COMPARATIVO: JUROS SIMPLES X
JUROS COMPOSTOS
1600,00
1800,00
2000,00
1200,00
1100,00
1000,00
1400,00
1095,45
1200,00
1000,00
1440,00
2488,80
2074,00
1728,00
0,00
500,00
1000,00
1500,00
2000,00
2500,00
3000,00
1 2 3 4 5 6 7
TEMPO (ANOS)
MONTANTE

18. Prof.Ilydio Sá 24
Montante
O cálculo do montante, em juros compostos é
dado pela fórmula:
n
)i.(CM += 1
M = montante ao fim de “n” períodos
C = capital inicial
n = número de períodos
i = taxa de juros por período, efetiva
F = fator de correção da taxa i
n
C.FM =

19. Prof.Ilydio Sá 25
Exemplo
Uma pessoa toma $ 1.000,00 emprestado sob taxa efetiva
2% a.m. pelo prazo de 10 meses com capitalização
composta. Qual o montante a ser devolvido ?
Resolução: C = 1.000
i = 2% a .m.
n = 10 meses
Temos:
$1.218,99M
2)1.000.(1,0M
C.FM
i)C.(1M
10
10
0
n
=∴
=
=
+=

20. Prof.Ilydio Sá 26
Valor Atual e Valor
Nominal
• O Valor Atual corresponde ao valor da aplicação
em uma data inferior à do vencimento.
• O Valor Nominal é o valor do título na data do
seu vencimento.
V = valor atual
N = valor nominal
i = taxa de juros
n = número de períodos que antecedem o vencimento do título
n
i
N
V
)1( +
=

21. Prof.Ilydio Sá 27
Exemplo
a) Por quanto devo comprar um título, vencível daqui a 5 me-
ses, com valor nominal de $ 1.131,40, se a taxa de juros com-
postos corrente for de 2,5% a.m. ?
Resolução:
n = 5 Meses
N=1.131,40
V

22. Prof.Ilydio Sá 28
N = 1.131,40
i = 2,5 % a.m.
n = 5 meses
00,000.1$
131408,1
40,131.1
)025,1(
40,131.1
)1(
5
≅
≅=
+
=
V
V
i
N
V n
Portanto, se comprar o título por $ 1.000,00, não esta-
rei fazendo mau negócio.

23. Prof.Ilydio Sá 29
Exemplo
b) Uma pessoa possui uma letra de câmbio que vence daqui a
1 ano, com valor nominal de $ 1.344,89. Foi-lhe proposta a tro-
ca daquele título por outro, vencível daqui a 3 meses e no valor
de $ 1.080,00. Sabendo-se que a taxa corrente de mercado é
de 2,5% a.m., pergunta-se se a troca proposta é vantajosa.
Resolução:
N=1.344,89
N*
=1.080,00
0 3 12

24. Prof.Ilydio Sá 30
Exemplo
O valor atual na data focal zero da letra de câmbio que vence
em 12 meses é dado por:
1
12 12
1
1
1344,89
(1 ) (1,025)
1.344,89
1.000,00
1,344889
$1.000,00
N
V
i
V
V
= =
+
= ≅
∴ =
Calculemos agora o valor atual na data zero, da letra que vence
em 3 meses:
2
3 3
* 1080,00
(1 ) (1,025)
N
V
i
= =
+

25. Prof.Ilydio Sá 31
Comparando os dois valores atuais constatamos que:
12 VV >
89,002.1$
076891,1
00,080.1
2
2
=∴
=
V
V
Ou seja, o título que vence em 3 meses tem um valor atual um
pouco maior que o que vence em 12 meses. Portanto, a troca
seria vantajosa.

26. TAXAS COMPOSTAS
Os diversos tipos de taxas para juros
compostos.

27. Prof.Ilydio Sá 33
TAXA NOMINAL
É uma taxa “simbólica” para juros compostos e usada apenas como
referência para cálculos rápidos da taxa efetiva. É fácil determinar
quando a taxa é nominal, pois ela estará sempre referida a uma
unidade de tempo, distinta da unidade que define o período de
capitalização. Ex: 24% ao ano, com capitalização mensal.
TAXA EFETIVA
É a taxa de juros compostos que já está referida à mesma unidade de
tempo que o período de capitalização. Ex: 1% ao mês, com
capitalização mensal; 24% ao ano, com capitalização anual; 0,5%
quinzenal, com capitalização quinzenal.
Importante: A passagem da taxa nominal para a taxa efetiva (que é a
usada na fórmula dos juros compostos) é feita de modo proporcional,
como nos juros simples, por convenção, para facilitar os cálculos.
24% ao ano, com
capitalização mensal
TAXA NOMINAL
24%:12 = 2% ao mês, com
capitalização mensal
TAXA EFETIVA

28. Prof.Ilydio Sá 34
Exemplo: Um capital de R$ 5000,00 foi investido, capitalizado
trimestralmente, sob taxa de 20% ao ano. Obtenha o montante final
dessa aplicação, sabendo-se que ela foi feita por um prazo de 2 anos.
20% ao ano, com
capitalização trimestral
TAXA NOMINAL
20%:4 = 5% ao trimestre
TAXA EFETIVA
7387,27(1,05)x5000M 8
==
2 anos = 8 trimestres
Lembre-se: Você nunca poderá usar a TAXA NOMINAL nos cálculos
com juros compostos.

29. Prof.Ilydio Sá 35
TAXAS EQUIVALENTES
São taxas efetivas, que geram montantes iguais, aplicadas ao mesmo
capital e no mesmo prazo.
Exemplo: 4% ao mês é equivalente a 8,16% ao bimestre. Veja, por
exemplo, que se aplicarmos essas duas taxas sobre um capital de
R$ 1000,0, para um investimento de um ano, vão gerar os seguintes
montantes:
4% ao mês
1601,03(1,04)x1000M 12
==
8,16% ao bimestre
1601,03(1,0816)x1000M 6
==
Na prática, quando queremos determinar uma taxa que seja
equivalente a outra, com capitalização distinta, usamos apenas os
fatores de correção, já que ao igualar os montantes, os capitais (que
são iguais) serão cancelados. Vejamos dois exemplos disso.

30. Prof.Ilydio Sá 36
EX. 1: Qual a taxa bimestral equivalente a 15,9693% ao
ano?
Como um ano tem 6 bimestres, é claro que o fator
bimestral (procurado), elevado ao expoente 6, terá de ser
igual ao fator anual, vejamos:
a.b2,5%procuradataxa
1,0251,159693F
1,159693FFF
6
b
6
ba
6
b
=
≅=
=⇒=
EX. 2: Qual a taxa mensal equivalente a 0,05% ao dia?
1,51%mensaltaxa
1,0151(1,0005)F
FF
30
m
30
dm
=
≅=
=