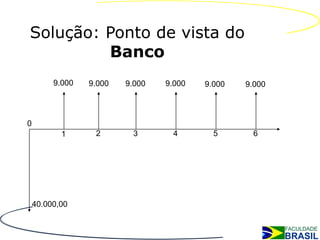
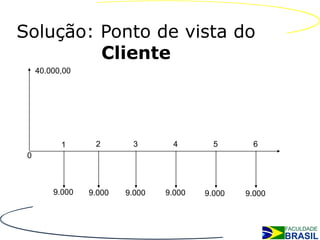
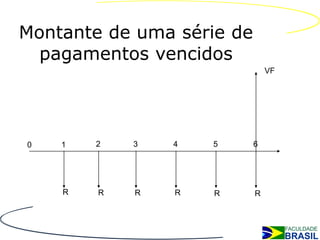
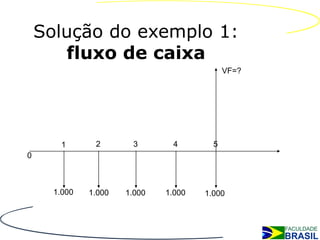
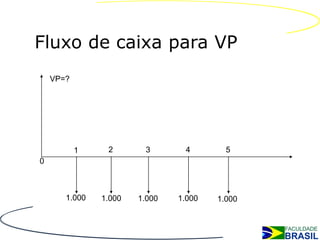
O documento discute séries de pagamentos, apresentando exemplos de fluxo de caixa do ponto de vista do banco e do cliente em um empréstimo de $40.000 em 6 parcelas iguais. Também apresenta tipos de séries de pagamentos, aplicações e cálculos como montante, valor presente e valor das parcelas.

1. Séries de Pagamentos

2. Noções de Fluxo de Caixa
• É uma sucessão de pagamentos e
recebimentos em dinheiro previstos
para uma determinada data ou período.
• O fluxo de caixa é representado por um
gráfico que indica o recebimento com
uma seta para cima e o pagamento com
uma seta para baixo.

3. Exemplo de fluxo de caixa
• Um banco concede um empréstimo de
$40.000,00 a um cliente, para pagamento
em seis parcelas iguais de $9.000,00.
• Representar o fluxo de caixa (a) do ponto
de vista do banco e (b) do ponto de vista do
cliente.

4. Solução: Ponto de vista do
Banco
9.000 9.000 9.000 9.000 9.000 9.000
0
1 2 3 4 5 6
40.000,00

5. Solução: Ponto de vista do
Cliente
40.000,00
1 2 3 4 5 6
0
9.000 9.000 9.000 9.000 9.000 9.000

6. Tipos de Séries de Pagamentos
1. Série de pagamentos iguais com termos
vencidos (postecipadas);
2. Série de pagamentos iguais com termos
antecipados;
3. Série de pagamentos variáveis com termos
vencidos;
4. Série de pagamentos variáveis com termos
antecipados.

7. Observações
1. A diferença de prazo entre dois termos
consecutivos é sempre constante;
2. O número de termos é finito (quando o
número de termos é infinito trata-se de
rendas perpétuas que não será tratado neste
tópico).
3. Os cálculos são baseados no sistema de
capitalização composta (juros compostos).

8. Aplicações das séries de
pagamentos
 Financiamento de veículos e imóveis
Investimento em poupança, fundos, etc
Compras com pagamento parcelado
Empréstimos

9. Exemplo 1

10. Exemplo 2

11. Tipos de cálculos que
podemos efetuar
• Montante acumulado após uma série de
aplicações;
• O valor de cada termo para formar um
montante desejado;
• Valor presente de uma série de pagamentos;
• Número de termos para formar um montante
com taxa e prestações conhecidas;
• Taxa de juros de uma série de pagamentos.

12. Montante de uma série de
pagamentos vencidos
VF
0 1 2 3 4 5 6
R R R R R R

13. Cálculo do montante de uma
série de pagamentos vencidos
VF  R
1  i  n
1
i
R = valor de cada parcela
i = taxa de juros
n = número de parcelas

14. Exemplo 1
Determinar o valor do montante, no final do
5º mês, de uma série de 5 aplicações
mensais, iguais e consecutivas, no valor de
$1000,00 cada uma, a uma taxa de 4% ao
mês, sabendo-se que a primeira parcela é
aplicada no final do primeiro mês, ou seja, a
30 dias da data tomada como base, e que a
última, no final do 5º mês, é coincidente com
o momento em que é pedido o montante.

15. Solução do exemplo 1:
fluxo de caixa
VF=?
1 2 3 4 5
0
1.000 1.000 1.000 1.000 1.000

16. Continuação da solução
VF  R
1  i  n
1
 1000
1  0,04  5
1
 5416 ,32
i 0,04

17. Exercícios
01. Qual o montante, no final de 8 meses,
referente a uma aplicação de $ 1.000,00 por
mês, à taxa de 3% a.m.? $ 8.892,34
02. Quanto deverá ser aplicado, a cada 2
meses, em um “Fundo de Renda Fixa”, à taxa
de 5% a.b., durante 3 anos e meio, para que
se obtenha, no final desse prazo, um
montante de $ 175.000,00?
$ 4.899,32

18. Cálculo do VP para série de
pagamentos constantes
postecipados
• E se no exemplo anterior, ao invés
do Valor Futuro (VF) pedíssemos o
Valor Presente (VP)?
• Como encontrar VP?

19. Fluxo de caixa para VP
VP=?
1 2 3 4 5
0
1.000 1.000 1.000 1.000 1.000

20. Mais uma Fórmula!!!
• Sabemos que VF = VP (1+i)n .
• Sabemos também que
VF  R
1  i n  1
i
• Assim
VP(1  i ) n
R
1  i  n
1
i

21. Portanto:
VP  R
1  i n
1
i (1  i ) n

22. E em nosso exemplo:
VP  R
1  i   1  1000 1  0,04   1
n 5
 ????
i1  i  0,041  0,04 
n 5
$ 4.451,82

23. Exercícios
03. Calcular o valor atual de uma série de 24
prestações iguais, mensais e consecutivas de
$ 3.500,00 cada uma, considerando uma taxa
de 5% a.m. $ 48.295,24
04. Um empréstimo de $30.000,00 é
concedido por uma instituição financeira para
ser liquidado em 12 prestações iguais,
mensais e consecutivas. Sabendo-se que a
taxa de juros é 3,5% a.m., calcular o valor da
prestação. $ 3.104,52

24. Na HP 12C
• Série de pagamentos
postecipados
(vencidos)
Utilize END
(Teclas: g - END)
• Série de pagamentos
antecipados
Utilize BEGIN
( Teclas: g - BEG)

25. NA HP 12C...
• PMT – parcelas.
• n – prazo,
quantidade de
parcelas.
• FV – valor futuro.
• i – taxa de juros
(em porcentagem)
de acordo com as
parcelas.