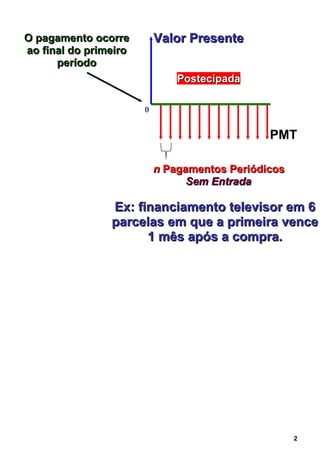
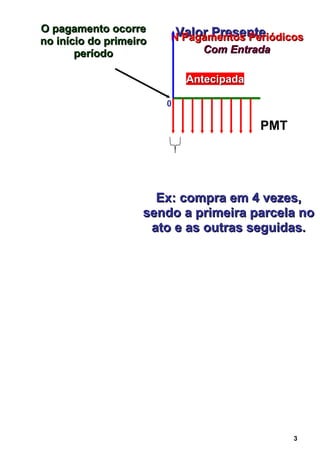
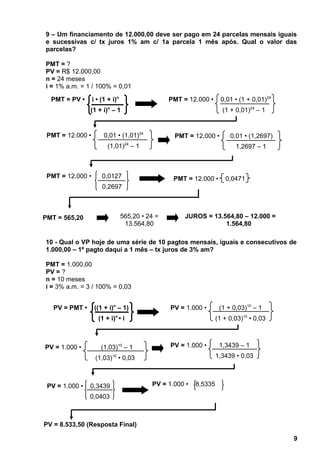
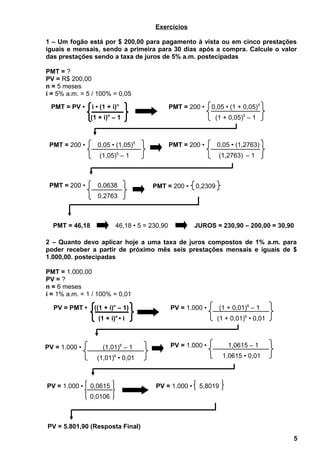
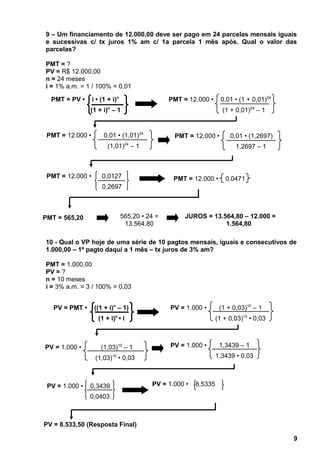
1. O documento discute séries uniformes de pagamentos, que consistem em uma sequência de valores iguais recebidos ou pagos ao longo do tempo. 2. Apresenta as fórmulas para cálculo de valor presente, valor futuro e prestação em séries uniformes postecipadas e antecipadas. 3. Fornece exemplos numéricos para exercitar o cálculo dessas grandezas usando as fórmulas apresentadas.

1. OPERAÇÕES COM SÉRIES UNIFORMES
Até agora, nós vimos:
- Na aplicação – aplica e resgata
- No empréstimo – recebe e devolve
- Operação de Desconto – você antecipa resgate ou vencimento
Prestações de crediários, crédito pessoal, CDC, financiamento imobiliário, etc
TIPOS DE SÉRIES DE PAGAMENTOS
Série Uniforme
- termos são iguais. Ex: 8 prestações mensais fixas para a compra de um
eletrodoméstico.
Série Variável
- séries de pagtos termos diferentes que guardam relação entre si. Ex:
financiamento imobiliário cujas parcelas observam razão crescimento.
Série Limitada
- quando o nº termo é finito.
Série Ilimitada
- quando nº termos é não finito. Ex: processo de automação. Valores custos
mensais de pessoal economizado.
Operações com Séries Uniformes
Consistem em uma seqüência de recebimentos ou pagamentos cujos valores são
iguais.
Usa o Regime de Capitalização Composta
Genericamente, as séries uniformes podem ser representadas de acordo com a figura
seguinte:
1
VP = ValorVP = Valor
PresentePresente
n = número de pagamentos iguaisn = número de pagamentos iguaisCarênciaCarência
mm + 1+ 1
PMT = Prestações ou PagamentosPMT = Prestações ou Pagamentos
0

2. 2
Valor PresenteValor Presente
nn Pagamentos PeriódicosPagamentos Periódicos
Sem EntradaSem Entrada
0
PostecipadaPostecipada
PMT
O pagamento ocorreO pagamento ocorre
ao final do primeiroao final do primeiro
períodoperíodo
Ex: financiamento televisor em 6Ex: financiamento televisor em 6
parcelas em que a primeira venceparcelas em que a primeira vence
1 mês após a compra.1 mês após a compra.

3. 3
Valor PresenteValor PresenteN Pagamentos PeriódicosN Pagamentos Periódicos
Com EntradaCom Entrada
0
AntecipadaAntecipada
PMT
O pagamento ocorreO pagamento ocorre
no início do primeirono início do primeiro
períodoperíodo
Ex: compra em 4 vezes,Ex: compra em 4 vezes,
sendo a primeira parcela nosendo a primeira parcela no
ato e as outras seguidas.ato e as outras seguidas.

4. Fórmulas
Postecipadas
PMT = PV . i . (1 + i)n
(1 + i)n
- 1
FV = PMT . ((1 + i)n
- 1)
i
PV = PMT . ((1 + i)n
- 1)
(1 + i)n
. i
Antecipadas
PMT = PV . i . (1 + i)n
x 1
(1 + i)n
- 1 (1 + i)
FV = PMT . ((1 + i)n
- 1) x (1 + i)
i
PV = PMT . ((1 + i)n
- 1) x (1 + i)
(1 + i)n
. i
4

5. Exercícios
1 – Um fogão está por $ 200,00 para pagamento à vista ou em cinco prestações
iguais e mensais, sendo a primeira para 30 dias após a compra. Calcule o valor
das prestações sendo a taxa de juros de 5% a.m. postecipadas
PMT = ?
PV = R$ 200,00
n = 5 meses
i = 5% a.m. = 5 / 100% = 0,05
2 – Quanto devo aplicar hoje a uma taxa de juros compostos de 1% a.m. para
poder receber a partir de próximo mês seis prestações mensais e iguais de $
1.000,00. postecipadas
PMT = 1.000,00
PV = ?
n = 6 meses
i = 1% a.m. = 1 / 100% = 0,01
5
PMT = PV • i • (1 + i)n
(1 + i)n
– 1
PMT = 200 • 0,05 • (1 + 0,05)5
(1 + 0,05)5
– 1
PMT = 200 • 0,05 • (1,05)5
(1,05)5
– 1
PMT = 200 • 0,05 • (1,2763)
(1,2763) – 1
PMT = 200 • 0,0638
0,2763
PMT = 200 • 0,2309
PMT = 46,18 46,18 • 5 = 230,90 JUROS = 230,90 – 200,00 = 30,90
PV = PMT • ((1 + i)n
– 1)
(1 + i)n
• i
PV = 1.000 • (1 + 0,01)6
– 1
(1 + 0,01)6
• 0,01
PV = 5.801,90 (Resposta Final)
PV = 1.000 • (1,01)6
– 1
(1,01)6
• 0,01
PV = 1.000 • 1,0615 – 1
1,0615 • 0,01
PV = 1.000 • 0,0615
0,0106
PV = 1.000 • 5,8019

6. 3 – Calcular o valor do resgate referente à aplicação de 12 parcelas mensais e
iguais de $ 600,00 a uma taxa de juros compostos de 2% a.m. postecipadas
PMT = 600,00
FV = ?
n = 12 meses
i = 2% a.m. = 2 / 100% = 0,02
4 – Quanto devo aplicar mensalmente à tx de juros compostos de 1,5% a.m. para
poder resgatar daqui a 6 meses a quantia de $ 3.000,00? Postecipadas.
PMT = ?
FV = 3.000,00
n = 6 meses
i = 1,5% a.m. = 1,5 / 100% = 0,015
6
FV = 600 • 13,41
FV = 8.046,00 (Resposta Final)
FV = PMT • ((1 + i)n
– 1)
i
FV = 600 • (1 + 0,02)12
– 1
0,02
FV = 600 • (1,02)12
– 1
0,02
FV = 600 • 1,2682 – 1
0,02
FV = 600 • 0,2682
0,02
PMT = 481,80 (Resposta Final)
FV = PMT • ((1 + i)n
– 1)
i
3.000 = PMT • (1 + 0,015)6
– 1
0,015
3.000 = PMT • (1,015)6
– 1
0,015
3.000 = PMT • 1,0934 – 1
0,015
3.000 = PMT • 0,0934
0,015
3.000 = PMT • 6,2267
PMT = 3.000
6,2267

7. 5 - Uma máquina de cortar grama é anunciada por $1.000,00 à vista ou em 4
parcelas mensais iguais sem entrada. A taxa de juros cobrada pela loja é igual a
2,00 % a.m. Qual o valor das prestações?
PMT = ?
PV = R$ 1.000,00
n = 4 meses
i = 2% a.m. = 2 / 100% = 0,02
6 - Uma máquina de cortar grama é anunciada por $1.000,00 à vista ou em 4
parcelas mensais iguais com entrada. A taxa de juros cobrada pela loja é igual a
2,00 % a.m. Qual o valor das prestações? (ANTECIPADAS)
7
PMT = PV • i • (1 + i)n
(1 + i)n
– 1
PMT = 1.000 • 0,2621
PMT = 262,10 262,10 • 4 = 1.048,40 JUROS = 1.048,40 – 1.000,00 =
48,40
PMT = 1.000 • 0,02 • (1 + 0,02)4
(1 + 0,02)4
– 1
PMT = 1.000 • 0,02 • (1,02)4
(1,02)4
– 1
PMT = 1.000 • 0,02 • (1,0824)
1,0824 – 1
PMT = 1.000 • 0,0216
0,0824

8. 7 – Qual o valor geral por 36 depósitos mensais iguais e consecutivos de 3.000,00
se o 1º for efetuado daqui a 1 mês c/ tx juros de 0,5% am? (POSTECIPADA)
PMT = 3.000,00
FV = ?
n = 36 meses
i = 0,5% a.m. = 0,5 / 100% = 0,005
8 – Qual o valor de cada um dos 15 depósitos iguais, mensais, consecutivos, se o
1º for daqui a 1 mês, necessários para gerar no final 15 meses um VF=96.581,37,
considerando tx juros 1% am
PMT = ?
FV = 96.581,37
n = 15 meses
i = 1% a.m. = 1 / 100% = 0,01
8
FV = 3.000 • 39,34
FV = 118.020,00 (Resposta Final)
FV = PMT • ((1 + i)n
– 1)
i
FV = 3.000 • (1 + 0,005)36
– 1
0,005
FV = 3.000 • (1,005)36
– 1
0,005
FV = 3.000 • 1,1967 – 1
0,005
FV = 3.000 • 0,1967
0,005
FV = PMT • ((1 + i)n
– 1)
i
96.581,37 = PMT • (1 + 0,01)15
– 1
0,01
96.581,37 = PMT • (1,01)15
– 1
0,01
96.581,37 = PMT • 1,161 – 1
0,01
96.581,37 = PMT • 0,161
0,01
96.581,37 = PMT • 16,1
PMT = 5.998,84 (Resposta Final)PMT = 96.581,37
16,1

9. 9 – Um financiamento de 12.000,00 deve ser pago em 24 parcelas mensais iguais
e sucessivas c/ tx juros 1% am c/ 1a parcela 1 mês após. Qual o valor das
parcelas?
PMT = ?
PV = R$ 12.000,00
n = 24 meses
i = 1% a.m. = 1 / 100% = 0,01
10 - Qual o VP hoje de uma série de 10 pagtos mensais, iguais e consecutivos de
1.000,00 – 1º pagto daqui a 1 mês – tx juros de 3% am?
PMT = 1.000,00
PV = ?
n = 10 meses
i = 3% a.m. = 3 / 100% = 0,03
9
PV = 1.000 • 8,5335
PMT = PV • i • (1 + i)n
(1 + i)n
– 1
PMT = 565,20 565,20 • 24 =
13.564,80
JUROS = 13.564,80 – 12.000 =
1.564,80
PMT = 12.000 • 0,01 • (1 + 0,01)24
(1 + 0,01)24
– 1
PMT = 12.000 • 0,01 • (1,01)24
(1,01)24
– 1
PMT = 12.000 • 0,01 • (1,2697)
1,2697 – 1
PMT = 12.000 • 0,0127
0,2697
PMT = 12.000 • 0,0471
PV = PMT • ((1 + i)n
– 1)
(1 + i)n
• i
PV = 1.000 • (1 + 0,03)10
– 1
(1 + 0,03)10
• 0,03
PV = 8.533,50 (Resposta Final)
PV = 1.000 • (1,03)10
– 1
(1,03)10
• 0,03
PV = 1.000 • 0,3439
0,0403
PV = 1.000 • 1,3439 – 1
1,3439 • 0,03

10. 9 – Um financiamento de 12.000,00 deve ser pago em 24 parcelas mensais iguais
e sucessivas c/ tx juros 1% am c/ 1a parcela 1 mês após. Qual o valor das
parcelas?
PMT = ?
PV = R$ 12.000,00
n = 24 meses
i = 1% a.m. = 1 / 100% = 0,01
10 - Qual o VP hoje de uma série de 10 pagtos mensais, iguais e consecutivos de
1.000,00 – 1º pagto daqui a 1 mês – tx juros de 3% am?
PMT = 1.000,00
PV = ?
n = 10 meses
i = 3% a.m. = 3 / 100% = 0,03
9
PV = 1.000 • 8,5335
PMT = PV • i • (1 + i)n
(1 + i)n
– 1
PMT = 565,20 565,20 • 24 =
13.564,80
JUROS = 13.564,80 – 12.000 =
1.564,80
PMT = 12.000 • 0,01 • (1 + 0,01)24
(1 + 0,01)24
– 1
PMT = 12.000 • 0,01 • (1,01)24
(1,01)24
– 1
PMT = 12.000 • 0,01 • (1,2697)
1,2697 – 1
PMT = 12.000 • 0,0127
0,2697
PMT = 12.000 • 0,0471
PV = PMT • ((1 + i)n
– 1)
(1 + i)n
• i
PV = 1.000 • (1 + 0,03)10
– 1
(1 + 0,03)10
• 0,03
PV = 8.533,50 (Resposta Final)
PV = 1.000 • (1,03)10
– 1
(1,03)10
• 0,03
PV = 1.000 • 0,3439
0,0403
PV = 1.000 • 1,3439 – 1
1,3439 • 0,03