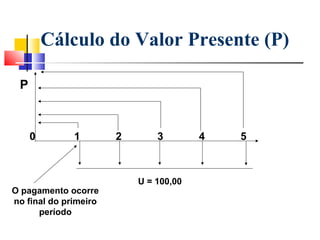
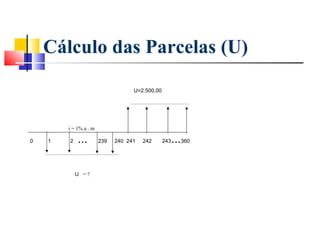
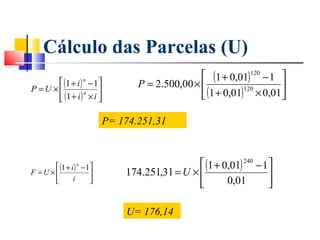
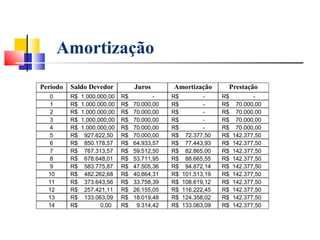
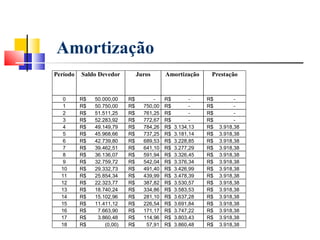
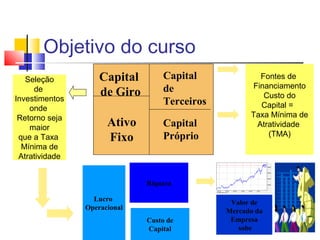
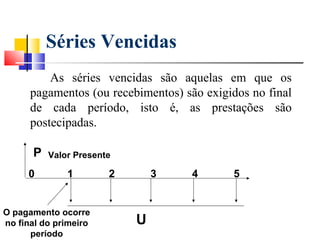
Este documento fornece um resumo do curso "Análise Econômica de Investimentos". O curso abordará conceitos básicos de matemática financeira como juros simples e compostos, além de métodos de análise de investimentos como VPL, TIR e VAN. O objetivo é capacitar os alunos a realizarem estudos de viabilidade econômica de projetos de investimento.

1. Análise Econômica de
Investimentos
Prof. Vallim

2. Agenda
 Objetivo do curso
 Conteúdo Programático
 Bibliografia
 Critérios de Notas

3. Objetivo do curso
Capacitar os alunos a elaborar
estudos de viabilidade econômica
de projetos de investimentos

4. Objetivo do curso
 A Análise Econômica de Investimentos é
uma técnica que possibilita quantificar
monetariamente e avaliar economicamente
alternativas de investimento;
 Permite ao gestor a posse de um conjunto
de elementos para a correta tomada de
decisão

5. Objetivo do curso
Exemplos de tomada de decisão :
 Investimentos (onde aplicar?).
 Produção (substituição/reforma de
equipamentos; expansão de capacidade);
 Lançamento de produtos;
 Aquisições/fusões.
 Terceirização.
 Plano de negócios

6. Objetivo do curso
Seleção Capital Capital Fontes de
de de Financiamento
Investimentos
de Giro Custo do
Terceiros Capital =
onde
Retorno seja Taxa Mínima de
maior
Ativo Capital Atratividade
Próprio (TMA)
que a Taxa Fixo
Mínima de
Atratividade
Riqueza
Lucro Valor de
Operacional Mercado da
Custo de Empresa
Capital sobe

7. Conteúdo Programático
Parte 1- Matemática financeira:
- Juros simples
- Juros compostos
- Séries uniformes de pagamentos.
Parte 2- Análise Econômica de investimentos.
- Inflação e correção monetária
- métodos de análise de investimentos (Pay-back;
VPL, TIR, VAU).
- Análise de projetos

8. Bibliografia
Newnan, D. G. ; Lavelle, J. P. Fundamentos de
Engenharia Econômica. LTC editora, Rio de Janeiro, 2000
MOTTA, Regis da Rocha; CALÔBA, Guilherme. Análise de
Investimentos: tomada de decisões de projetos
industriais. São Paulo : Atlas, 2002.
Pilão N. E. ; Hummel P. R. V. Matemática Financeira
e Engenharia Econômica - Ed.Pioneira -Thomson, 2006
Puccini, A .L.Matemática Financeira, objetiva e aplicada.
Saraiva, S.Paulo, 2002

9. Critério de Notas
Média = ( P1 x 0,30 ) + ( P2 x 0,70)
Média = ( P1 x 0,30 ) + ( P3 x 0,70)
Média = ( P2 x 0,50 ) + ( P3 x 0,50)

10. Análise Econômica de
Investimentos
Matemática Financeira:
Capitalização Simples

11. Conteúdo Programático
Conceitos básicos
Juros simples
Taxa proporcional
Exercícios resolvidos

12. Conceitos básicos
Princípio fundamental
O valor do dinheiro no tempo.
Por que ?
Custo de oportunidade
Juros – remuneração do
Aluguel do capital capital por período de tempo

13. Conceitos básicos
Observação :
O juro deve estar sempre associado ao período de tempo.
a.a. = ao ano;
a.m.= ao mês;
Exemplo :
10% a.a. = 10% ao ano;
1,5% a.m. = 1,5% ao mês.

14. Conceitos básicos
 Valor Presente (P)
 Juros (J)
 Taxa de Juros (i)
 Prazo (n)
 Valor Futuro (F)

15. Conceitos básicos
• Diagrama de Fluxos de Caixa:
Maneira esquemática de representar operações financeiras ao longo do tempo,
demonstrando todas as “entradas” (receitas) e “saídas” (despesas) de recursos.
Por convenção, as “entradas” são representadas como setas para cima, sendo o
inverso para as “saídas”.
“Entrada de Caixa”
0 Linha do tempo n
“Saída de Caixa”

16. Juros Simples
No regime de capitalização simples ou
linear, a taxa de juros (i) incide apenas
sobre o capital inicial (P).
Valor Futuro
P
Tempo

17. Juros Simples
Exemplo: Consideremos a aplicação de
R$100,00, por três anos, à taxa anual de 10%.
n P J (i = 10%)
1 R$100,00 R$10,00
2 R$100,00 R$10,00
3 R$100,00 R$10,00
Total dos juros auferidos em 03 períodos = 30

18. Juros Simples
J=Pxixn
n= 3 F
0
P
$ 100 i= 10% a .a
J=Pxixn
J = 100 x 0,10 x 3
J = $ 30

19. Juros Simples
J=Pxixn
F =P + ⇒ =F −
J J P
Igualando as equações , teremos que:
F − =P × × ⇒ =P + × ×
P i n F P i n
Finalmente
F =P(1 + × )
i n

20. Juros Simples
Exercício: Quanto ganhou de juros um
aplicador que depositou $ 3.000,00 por
um ano à taxa de juros simples de 25%
a.a.?
Solução: P = 3.000, i = 25% a.a. e queremos saber J.
Pela equação (2) temos que J = P x i x n, logo:
J = 3.000 x 0,25 x 1 = $ 750

21. Juros Simples
Exercício: Qual o valor de resgate (montante)
de uma aplicação de $ 1.600 feita por um ano
à taxa de juros simples de 15% a.a.?
Solução: P = 1.600, i = 50% a.a. e queremos saber F.
J = P x i x n, logo:
J = 1.600 x 0,15 x 1 = $ 240
F = P + J, então:
F = 1.600 + 240 = $ 1.840
Poderíamos resolver o problema, ainda, utilizando a equação :
F = P x (1 + i). Desta forma, teríamos:
F = 1.600 x (1 + 0,15) = $ 1.840

22. Juros Simples
Exercício: Quanto renderia um capital
de $ 10.000 aplicado por dois meses à
taxa simples de 18% a.a.?
Solução: P = 10.000, n = 2 meses, i = 18% a.a. e queremos
saber J.
J = P x i x n = 10.000 x (0,18/12) x 2 = $ 300

23. Análise Econômica de
Investimentos
Matemática Financeira:
Capitalização Composta

24. Conteúdo Programático
Capitalização composta
- Cálculo do Valor Futuro (F)
- Cálculo do Valor Presente (P)
- Cálculo da taxa (i)
- Cálculo do prazo (n)
Tipos de Taxas de Juros
- Taxa Nominal
- Taxa Efetiva

25. Capitalização Composta
A capitalização composta é aquela
em que a taxa de juros incide sempre
sobre o capital inicial, acrescido dos
juros acumulados até o período
anterior

26. Cálculo do Valor Futuro (F)
Exemplo: Qual seria o valor
futuro de uma aplicação de R$
1.000,00 a uma taxa de juros
compostos de 4% ao mês pelo
período de três meses. Nesse
caso, teríamos:
FV
0 1 2 3
i= 4%
PV = $ 1.000,00

27. Cálculo do Valor Futuro (F)
Capitalização Composta
Juros por período Montante
1.000,00 x 0,04= 40,00 1.040,00
1.040,00 x 0,04= 41,60 1.081,60
1.081,60 x 0,04= 43,26 1.124,86
P = 1.000,00
F1 = 1.000,00 + (0,04 x 1.000,00) = 1.000,00 (1+ 0,04)
F2 = F1 (1 + 0,04)  F2 = 1.000,00 (1 + 0,04) (1 + 0,04)
 F2 = 1.000,00 (1 + 0,04)2
F3 = F2 (1 + 0,04)  F3 = 1.000,00 (1 + 0,04)2 (1 + 0,04)
 F3 = 1.000,00 (1 + 0,04)3
F = 1.000,00 × (1 + 0,04 ) ⇒ F = 1.124,86
3

28. Cálculo do Valor Futuro (FV)
Generalizando, temos a seguinte fórmula :
F = P (1 + i)n
Onde:
F = Valor futuro
P = Valor presente
n = Número de períodos de capitalização
i = Taxa de juros.

29. Cálculo do Valor Futuro (F)
CAPITALIZAÇÃO SIMPLES CAPITALIZAÇÃO COMPOSTA
Capital no Capital e Capital no Capital e
começo de Juros ao juros ao começo ao Juros ao juros ao
cada período final de final de final de final de final de
de cada cada cada cada cada Variação
mês capitalização período período período período período %
1 100,00 1,50 101,50 100,00 1,50 101,50
2 100,00 1,50 103,00 101,50 1,52 103,02
3 100,00 1,50 104,50 103,02 1,55 104,57
4 100,00 1,50 106,00 104,57 1,57 106,14
5 100,00 1,50 107,50 106,14 1,59 107,73
6 100,00 1,50 109,00 107,73 1,62 109,34 0,32%
12 100,00 1,50 118,00 117,79 1,77 119,56 1,32%
24 100,00 1,50 136,00 140,84 2,11 142,95 5,11%
60 100,00 1,50 190,00 240,71 3,61 244,32 28,59%

30. Cálculo do Valor Presente (P)
Exemplo: Uma pessoa pretende
resgatar daqui a 24 meses o valor
de R$ 25.000,00 para comprar
um carro. Sabendo-se que essa
pessoa pode obter uma taxa de
1,0% ao mês no mercado
financeiro, pergunta-se: qual o
valor que ela deve aplicar hoje?
25.000,00 = P × (1 + 0,01) 24 ⇒ P = 19.689,15

31. Cálculo da Taxa (i)
Exemplo: Qual é a taxa de juros mensal
recebida por um investidor que aplica R$
5.000,00 e resgata R$ 5.788,13 no final de 3
meses.
5.788,13 = 5.000,00 × (1 + i ) ⇒ 5.788,13 ÷ 5.000,00 = (1 + i )
3 3
(1,78813)1 3 = (1 + i ) ⇒ (1,05) −1 = i ⇒ i = 0,05ou5%a.m

32. Cálculo do prazo (n)
Exemplo: Em que prazo um empréstimo de
R$ 55.000,00 pode ser liquidado em um único
pagamento de R$ 110.624,65, sabendo-se que
a taxa contratada é de 15% ao semestre.
110.624,65 = 55.000,00 × (1 + 0,15) ⇒ 110.624,65 ÷ 55.000,00 = (1 + 0,15)
n n
2,0114 = (1,15) ⇒ n = log 2,0114 ÷ log 0,15 ⇒ n = 5semestres
n

33. Exercícios Resolvidos
Exercício-Uma casa está sendo oferecida por R$
100.000,00 à vista ou R$ 30.000,00 de entrada e mais duas
parcelas, sendo a primeira de R$ 50.000,00 no final de 6
meses e mais uma de R$ 28.000,00 após 12 meses da data
da compra. Sabendo-se que no mercado financeiro a taxa
de juros composta é de 1,53% ao mês, determinar o valor
presente e a melhor opção para um interessado que possua
recursos disponíveis para comprá-la.

34. Exercícios Resolvidos
Valor Presente da Primeira parcela
50.000,00 = P × (1 + 0,0153) ⇒ P = 45.646,10
6
Valor Presente da Segunda parcela
28.000,00 = P × (1 + 0,0153) ⇒ P = 23.335,95
12
Valor Presente Total
P = 30.000,00 + 45.646,10 + 23.335,95 = R$ 98.982,05
Para podermos comparar valores eles, necessariamente, devem estar em uma mesma
data. Assim sendo, podemos concluir que a melhor opção para um interessado seria
comprar parcelado.

35. Tipos de Taxas de Juros
 Taxa Nominal
 Taxa Efetiva
 Taxa Equivalente

36. Tipos de taxa de juros
Definições :
Taxa de juros nominal : Em geral, é usada uma taxa proporcional
(linear) da taxa nominal de juros, calculada de acordo com algum
procedimento previamente estabelecido pelo mercado ou pelas partes
que realizam a operação.
Taxa de juros efetiva : é taxa de juros recebida ou paga de fato
(corresponde ao fator de variação obtido do diagrama de fluxo de
caixa da operação).

37. Tipos de taxa de juros
Exemplo: Considerando uma aplicação que paga juros nominais de
6% ao ano; a taxa mensal proporcional será de 6%/12 = 0,5% a .m
Uma aplicação de R$1.000,00 ao final de um ano, considerando a
capitalização mensal, renderá o montante de
1.000 × (1 + 0,005) = 1.061,68
12
Logo a taxa efetiva será de 1.061,68 − 1.000,00
= 0,0617
1000
Assim temos: 6% a.a. é a taxa nominal, 0,5% a.m. é a taxa proporcional e
6,17% é a taxa efetiva.

38. Taxa Equivalente
No regime de capitalização composta, duas
taxas de juros são equivalentes quando,
considerando o mesmo prazo de aplicação
e o mesmo capital, as duas taxa promovam
rendimentos iguais.

39. Taxa Equivalente
P × (1 + ia ) = P × (1 + im ) ⇒ (1 + ia ) = (1 + im )
12 12
i a = (1 + i m ) − 1
12
i m = (1 + i a )
1 12
−1
Taxa Equivalente (1 + iefetiva maior ) = (1 + iefetiva menor ) n
ou
iQ = (1 + iT )
Q
T −1

40. Taxa Equivalente
Exemplo: : Determine a taxa
anual equivalente a 2% ao mês
iQ = (1 + iT )
Q
Solução: T −1
(1 + 0,02) 12 − 1 = 0,2682
iq = 26,82% a.a.

41. Taxa Equivalente
Para comprovar que estas duas
taxas são equivalentes, vamos
calcular o valor futuro de uma
aplicação de R$ 1.000,00 pelo
prazo de 1 ano. Uma sendo
aplicado à taxa de 2% ao mês, e
uma outra de mesmo valor pelo
mesmo prazo a uma taxa de
26,824% ao ano.

42. Taxa equivalente
... F=?
1 2 9 10 12
0
i= 2% a m
P=1.000,00
F = 1.000,00 (1 + 0,02)12
FV = 1.268,24

43. Taxa equivalente
F=?
0
1 ano
i= 26,824% a a
P=1.000,00
F = 1.000,00 (1 + 0,26824)1
FV = 1.268,24

44. Taxa Equivalente
Exemplo: : Determine a taxa
mensal equivalente a 6% ao
trimestre
iQ = (1 + iT ) T − 1
Q
Solução:
(1 + 0,06)1/ 3 − 1 = 0,0196
iq = 1,96% a.m.

45. Taxa Equivalente
Exemplo : Calcule o valor de
resgate de uma aplicação de R$
24.000,00, considerando 9 meses
de prazo e uma taxa efetiva de
25% ao ano.

46. Taxa equivalente
... F=?
1 2 7 8 9
0
i= 1,88% a m
P=24.000,00
iQ = (1 + iT )
Q
T −1 F = 24.000,00 (1 + 0,0188)9
iQ = (1 + 0,25)
1
12 −1
iQ = 1,88% a.m FV = 28.372,25

47. Taxa equivalente
Exercício - Dona Maria possui um título que vencerá no
prazo de um ano. O valor de resgate desse título é de R$
2.000,00. Foi oferecida a ela uma proposta para trocar
aquele título por outro, com vencimento daqui a 7 meses,
sendo o seu valor de resgate de R$ 1.600,00. Considerando
que a taxa composta no mercado financeiro gira ao redor de
35% ao ano, a troca seria vantajosa para Dona Maria?
iQ = (1 + iT )
Q
T −1 F = 1.600,00 (1 + 0,0253)5
iQ = (1 + 0,35)
1
12 −1
F = 1.813,12
iQ =2,53% a.m
A troca não
deveria ser feita

48. Análise Econômica de
Investimentos
Matemática Financeira: Séries
uniformes de pagamento

49. Conteúdo Programático
Séries Uniformes
- Séries Vencidas
- Séries Antecipadas
- Séries Diferidas
- Amortização
- Gradiente

50. Séries Uniformes
Uma série uniforme de pagamentos
(recebimentos) implica o pagamento
ininterrupto e periódico de uma
prestação (U) por um período (1...n) e
uma taxa i.
0
1 2 3
n-1
n

51. Séries Vencidas
As séries vencidas são aquelas em que os
pagamentos (ou recebimentos) são exigidos no final
de cada período, isto é, as prestações são
postecipadas.
P Valor Presente
0 1 2 3 4 5
O pagamento ocorre
no final do primeiro U
período

52. Cálculo do Valor Futuro (F)
Exemplo: Determinar o valor
futuro, no final do 5º mês, de
uma série de 5 aplicações
mensais, iguais e consecutivas,
em um fundo de renda fixa, no
valor de R$ 1.000,00 cada uma,
a uma taxa de 1% ao mês

53. Cálculo do Valor Futuro (F)
F Valor Futuro
0 1 2 3 4 5
U = 1.000,00
O pagamento ocorre
no final do primeiro
período

54. Cálculo do Valor Futuro (F)
F1 = 1000 × (1 + 0,01) = 1.040,60
4
F2 = 1000 × (1 + 0,01) = 1.030,30
3
F3 = 1000 × (1 + 0,01) = 1.020,10
2
F4 = 1000 × (1 + 0,01) = 1.010,00
1
F5 = 1000 × (1 + 0,01) = 1.000,00
0
FTOTAL = 5.101,01

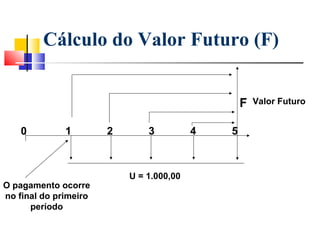
55. Cálculo do Valor Futuro (F)
[ 1 2 3 4
]
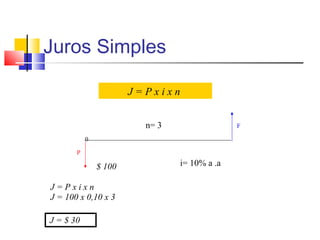
FTOTAL = 1000 × (1 + 0,01) + (1 + 0,01) + (1 + 0,01) + (1 + 0,01) + (1 + 0,01) = 5.101,01
0
 1× n − 1
a q a
P.G = 
 q− 1 
1× (1 + 0,01) 5 − 1
F = 1.000,00 ×   = 5.101,01
 (1 + 0,01) − 1 
 (1 + 0,01) 5 − 1
F = 1.000,00 ×   = 5.101,01
 ( 0,01) 

56. Cálculo do Valor Futuro (F)
FAC - Fator de acumulação de capital
F =U ×
(1 + i ) n
−1 F = U × FAC (n, i )
i

57. Cálculo do Valor Presente (P)
Exemplo: Calcular o valor a
vista de um bem vendido em 5
parcelas de R$ 100,00 sabendo-
se que se trata de uma série
vencida e que a taxa contratada
foi de 4% ao mês e que a
primeira parcela é aplicada no
final do primeiro mês

58. Cálculo do Valor Presente (P)
P
0 1 2 3 4 5
U = 100,00
O pagamento ocorre
no final do primeiro
período

59. Cálculo do Valor Presente (P)
1
P = 100,00 × = 100,00 × 0,96614 = 96,15
1
(1 + 0,04) 1
1
P2 = 100,00 × = 100,00 × 0,9256 = 92,46
(1 + 0,04) 2
1
P3 = 100,00 × = 100,00 × 0,8890 = 88,90
(1 + 0,04) 3
1
P4 = 100,00 × = 100,00 × 0,8548 = 85,48
(1 + 0,04) 4
1
P5 = 100,00 × = 100,00 × 0,82193 = 82,19
(1 + 0,04) 5
PTOTAL = R$445,18

60. Cálculo do Valor Presente (P)
FVA - Fator de valor presente (atual)
P =U ×
(1 + i ) − 1
n
P = U × FVA(n, i )
(1 + i ) × i
n
 (1 + 0,04 ) 5 − 1 
P = 100,00 ×   = 445,18
 (1 + 0,04 ) x0,04 
5

61. Cálculo das Parcelas (U)
Exemplo: O Sr. Carlos deseja
saber quanto ele deve aplicar
mensalmente, a partir do
próximo mês, para que daqui
a vinte anos, ele possa sacar
R$ 2.500,00 por mês, ao
longo de dez anos. A taxa de
juros efetiva de 1% a.m.

62. Cálculo das Parcelas (U)
U=2.500,00
i = 1% a . m
0 1 2 ... 239 240 241 242 243 ...360
U =?

63. Cálculo das Parcelas (U)
 (1 + 0,01) 120 − 1 
 (1 + i ) − 1 
n
P = 2.500,00 ×  
 (1 + 0,01) × 0,01
P =U ×
(1 + i ) n × i 
120
 
P= 174.251,31
 (1 + i ) − 1 
n  (1 + 0,01) 240 − 1
F =U ×
i
 174.251,31 = U ×  
 
 0,01 
U= 176,14

64. Séries Antecipadas
Uma série é dita antecipada quando os
pagamentos (ou recebimentos) são exigidos
no início de cada período de tempo. Assim, a
primeira prestação é sempre paga ou recebida
no momentos ZERO, ou seja, na data do
contrato do empréstimo, do financiamento ou
qualquer outra operação que implique
pagamentos ou recebimentos de prestações.

65. Séries Antecipadas
F =U
(1 + i ) n
−1
×(1 + i )
i
 (1 + i ) n − 1 
P =U ×  x(1 + i )
 (1 + i ) × i 
n

66. Cálculo do Valor Futuro (F)
Exemplo: Marina fez cinco
aplicações mensais de R$
1.000,00 em uma aplicação que
paga juros efetivos de 1% a.m.
Sabendo-se que a primeira
aplicação foi feita no ato,
pergunta-se: quanto ela terá
acumulado ao final de 5 meses?

67. Cálculo do Valor Futuro (F)
FV
F =U
(1 + i ) n − 1 × (1 + i )
0 1 2 3 4 5
i
1.000,00 1.000,00 1.000,00 1.000,00 1.000,00
 (1 + 0,01) 5 − 1
F = 1.000,00 ×   x(1 + 0,01) = 5.152,02
 ( 0,01) 

68. Cálculo do Valor Presente (P)
Exemplo: um televisor foi
vendido em oito prestações
mensais e iguais de R$ 515,74.
Sabendo-se que a primeira
parcela foi feita no ato (série
antecipada) e que a taxa de
juros composta cobrado foi de
5% a.m., calcule o valor
presente dessa televisão.

69. Cálculo do Valor Presente (P)
 (1 + i ) n − 1 
P =U ×  x(1 + i )
 (1 + i ) × i 
n
 (1 + 0,05) 8 − 1 
P = 515,74 x   x(1 + 0,05)
 (1 + 0,05) × 0,05 
8
P= 3.500,00

70. Séries Diferidas
As séries diferidas são caracterizadas pela existência de um
período de carência para efetuar o pagamento (ou
recebimento) da primeira prestação (termo). Em outras
palavras, o primeiro pagamento (ou recebimento) é efetuado
em data posterior àquela do primeiro período.
P
0 1 2 3 4 5
Carência
U

71. Séries Diferidas
Exemplo: uma empresa conseguiu um
financiamento no valor de R$
50.000,00. O empréstimo deverá ser
pago em 12 parcelas mensais, à taxa
de juros efetivos de 8% a.m. Sabendo-
se que o primeiro pagamento será
realizado no final do terceiro mês
(prazo de carência), calcule o valor
das prestações:

72. Séries Diferidas
F = 50.000,00 × (1 + 0,08) ⇒ F = 58.320,00
2
P = 50.000,00
i = 5% a.m
0 1 2 3 4 ... 11 12 13 14
U=?
 (1 + 0,08) 12 − 1 
58.320,00 = U × 
 (1 + 0,08)12 x0,08 

U= 7.738,77

73. Amortização
Exemplo: Elaborar a planilha
de amortização de um
empréstimo de R$100.000,00, à
taxa mensal de 1%, a ser pago
em 5 prestações mensais iguais
e sucessivas.
 (1 + 0,01) 5 − 1 
 (1 + i ) n − 1  100.000,00 = U ×  
 (1 + 0,01) × 0,01
5
P =U ×
 (1 + i ) n × i 

U= 20.603,98

74. Amortização
PLANO DE AMORTIZAÇÃO
N Saldo Devedor (SD) Juros (J) Amortização (A) Prestação (U)
0 100.000,00 - - -
1 80.396,02 1.000,00 19.603,98 20.603,98
2 60.596,00 803,96 19.800,02 20.603,98
3 40.597,98 605,96 19.998,02 20.603,98
4 20.399,98 405,98 20.198,00 20.603,98
5 0,00 204,00 20.399,98 20.603,98
Primeira prestação Segunda prestação
J1 = 0,01× 100.000 = 1.000,00 J 2 = 0,01× 80.396,02 = 803,96
A1 = U − J1 = 20.603,98 − 1.000,00 = 19.603,98 A2 = U − J 2 = 20.603,98 − 803,96 = 19.800,02
SD1 = 100.000,00 − 19.603,98 = 80.396,02 SD2 = 80.396,02 − 19.800,02 = 60.596,00
E assim sucessivamente até o final das prestações

75. Amortização
Exemplo : Um banco de investimento
oferece um financiamento de R$
1.000.000,00, com taxa de juros de 7% ao
semestre, nas seguintes condições: prazo
de 14 parcelas semestrais iguais e
sucessivas, sendo 4 semestres de carência;
pagamento integral dos juros devidos
durante o período de carência. Elabore a
planilha dessa operação:

76. Amortização
Período Saldo Devedor Juros Amortização Prestação
0 R$ 1.000.000,00 R$ - R$ - R$ -
1 R$ 1.000.000,00 R$ 70.000,00 R$ - R$ 70.000,00
2 R$ 1.000.000,00 R$ 70.000,00 R$ - R$ 70.000,00
3 R$ 1.000.000,00 R$ 70.000,00 R$ - R$ 70.000,00
4 R$ 1.000.000,00 R$ 70.000,00 R$ - R$ 70.000,00
5 R$ 927.622,50 R$ 70.000,00 R$ 72.377,50 R$ 142.377,50
6 R$ 850.178,57 R$ 64.933,57 R$ 77.443,93 R$ 142.377,50
7 R$ 767.313,57 R$ 59.512,50 R$ 82.865,00 R$ 142.377,50
8 R$ 678.648,01 R$ 53.711,95 R$ 88.665,55 R$ 142.377,50
9 R$ 583.775,87 R$ 47.505,36 R$ 94.872,14 R$ 142.377,50
10 R$ 482.262,68 R$ 40.864,31 R$ 101.513,19 R$ 142.377,50
11 R$ 373.643,56 R$ 33.758,39 R$ 108.619,12 R$ 142.377,50
12 R$ 257.421,11 R$ 26.155,05 R$ 116.222,45 R$ 142.377,50
13 R$ 133.063,09 R$ 18.019,48 R$ 124.358,02 R$ 142.377,50
14 R$ 0,00 R$ 9.314,42 R$ 133.063,09 R$ 142.377,50

77. Amortização
Exemplo : Um banco de investimento
oferece um financiamento de R$
50.000,00, com taxa de juros de 1,5% ao
mês, nas seguintes condições: prazo de
dezoito meses, sendo três meses de
carência; capitalização dos juros devidos
durante o período de carência. Elabore a
planilha de amortização referente dessa
operação:

78. Amortização
Período Saldo Devedor Juros Amortização Prestação
0 R$ 50.000,00 R$ - R$ - R$ -
1 R$ 50.750,00 R$ 750,00 R$ - R$ -
2 R$ 51.511,25 R$ 761,25 R$ - R$ -
3 R$ 52.283,92 R$ 772,67 R$ - R$ -
4 R$ 49.149,79 R$ 784,26 R$ 3.134,13 R$ 3.918,38
5 R$ 45.968,66 R$ 737,25 R$ 3.181,14 R$ 3.918,38
6 R$ 42.739,80 R$ 689,53 R$ 3.228,85 R$ 3.918,38
7 R$ 39.462,51 R$ 641,10 R$ 3.277,29 R$ 3.918,38
8 R$ 36.136,07 R$ 591,94 R$ 3.326,45 R$ 3.918,38
9 R$ 32.759,72 R$ 542,04 R$ 3.376,34 R$ 3.918,38
10 R$ 29.332,73 R$ 491,40 R$ 3.426,99 R$ 3.918,38
11 R$ 25.854,34 R$ 439,99 R$ 3.478,39 R$ 3.918,38
12 R$ 22.323,77 R$ 387,82 R$ 3.530,57 R$ 3.918,38
13 R$ 18.740,24 R$ 334,86 R$ 3.583,53 R$ 3.918,38
14 R$ 15.102,96 R$ 281,10 R$ 3.637,28 R$ 3.918,38
15 R$ 11.411,12 R$ 226,54 R$ 3.691,84 R$ 3.918,38
16 R$ 7.663,90 R$ 171,17 R$ 3.747,22 R$ 3.918,38
17 R$ 3.860,48 R$ 114,96 R$ 3.803,43 R$ 3.918,38
18 R$ (0,00) R$ 57,91 R$ 3.860,48 R$ 3.918,38

79. Gradiente (G)
Séries : Valor Presente/Futuro da série gradiente (G)
(N-1) G
3G
+2 G
+1 G
+0 G
t=0 Tempo
t=1 t=2 t=3 t=4 t=n
 (1 + i ) n − 1 − ni   (1 + i ) n − 1 n 
P = G 2  F = G − 
 i (1 + i )
n 2
  i i

80. Gradiente (G)
Exemplo – Calcular o valor presente da série gradiente dado que
i = 10% ao período.  (1 + i ) n − 1 − ni 
P = G 2 
60  i (1 + i ) n 
+40
 (1 + 0,1) 4 − 1 − 4 × 0,1
P = 20 ×  
+20
 0,12 (1 + 0,1) 4 
t=1 t=2 t=3 Tempo
t=0 t=4 P = 20 × 4,38 = 87,56
1 1 1
P = 20 × + 40 × + 60 ×
(1 + 0,1) 2 (1 + 0,1) 3 (1 + 0,1) 4
P = 20 × 0,826 + 40 × 0,751 + 60 × 0,683
P = 16,53 + 30,05 + 40,98 = 87,56

81. Tabelas