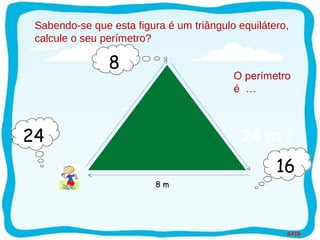
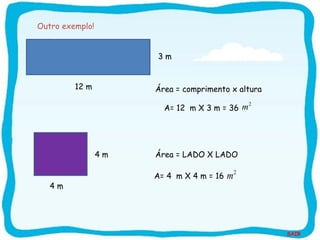
O documento discute conceitos de perímetro e área de figuras geométricas planas. Ele apresenta exemplos para ensinar os conceitos, incluindo medições de objetos reais para construir compreensão. O objetivo é que os alunos aprendam a calcular perímetro e área e reconheçam suas aplicações no cotidiano.