Baixado 171 vezes
Carregado porBetão Betão
Conjuntos Numericos 1209918617804865 9
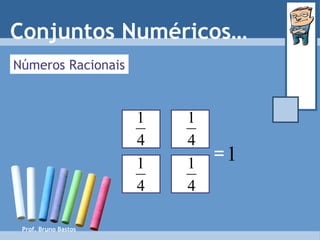
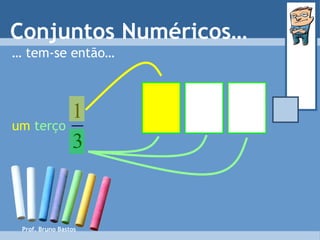
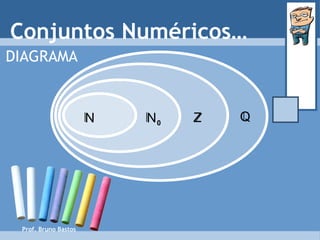
O documento discute diferentes conjuntos numéricos, incluindo números naturais, inteiros relativos, racionais e suas representações matemáticas. Explica como os números racionais podem ser expressos como frações com numerador e denominador inteiros e fornece exemplos.
Mais conteúdo relacionado
Semelhante a Conjuntos Numericos 1209918617804865 9
Conjuntos Numericos 1209918617804865 9
- 1.
- 2. Prof. Bruno BastosConjuntos Numéricos…
- 3. Prof. Bruno BastosO conceito de número foi evoluindo ao longo dos tempos, tendo-se criado novos números para responder a problemas entretanto surgidos. Conjuntos Numéricos…
- 4. Prof. Bruno BastosConjuntos Numéricos…
- 5. Prof. Bruno BastosNúmeros Naturais Conjuntos Numéricos…
- 6. Prof. Bruno BastosNúmeros Naturais A representação matemática deste conjunto é: Conjuntos Numéricos…
- 7. Prof. Bruno BastosNúmeros Naturais A representação matemática deste conjunto é: Conjuntos Numéricos… = { 1, 2, 3, 4, 5, 6, 7, 8 ... } N
- 8. Prof. Bruno BastosConjuntos Numéricos…
- 9. Prof. Bruno BastosNúmeros Inteiros Relativos Conjuntos Numéricos…
- 10. Prof. Bruno BastosNúmeros Inteiros Relativos A representação matemática deste conjunto é: Conjuntos Numéricos…
- 11. Prof. Bruno BastosNúmeros Inteiros Relativos A representação matemática deste conjunto é: Conjuntos Numéricos… = {..., -3, -2, -1, 0, 1, 2, 3, ...} Z
- 12. Prof. Bruno BastosNúmeros Inteiros Relativos Conjuntos Numéricos…
- 13. Prof. Bruno BastosConjuntos Numéricos… Números Inteiros Relativos e os subconjuntos de Z Z
- 14. Prof. Bruno BastosConjuntos Numéricos… Números Inteiros Relativos {0} = Z + Z - Z e os subconjuntos de Z Z
- 15. Prof. Bruno BastosConjuntos Numéricos… Números Inteiros Relativos = {..., -3, -2, -1} {0} = Z Z - + Z - Z e os subconjuntos de Z Z
- 16. Prof. Bruno BastosConjuntos Numéricos… Números Inteiros Relativos = {..., -3, -2, -1} = {1, 2, 3, 4, …} {0} = Z Z + Z - + Z - Z e os subconjuntos de Z Z
- 17. Prof. Bruno BastosConjuntos Numéricos…
- 18. Prof. Bruno BastosNúmeros Racionais Conjuntos Numéricos…
- 19. Prof. Bruno BastosNúmeros Racionais Números racionais são todos os números que podem ser escritos sob a forma de uma fracção com numerador e denominador inteiros. Conjuntos Numéricos…
- 20. Prof. Bruno BastosNúmeros Racionais Números racionais são todos os números que podem ser escritos sob a forma de uma fracção com numerador e denominador inteiros. Conjuntos Numéricos…
- 21. Prof. Bruno BastosNúmeros Racionais Números racionais são todos os números que podem ser escritos sob a forma de uma fracção com numerador e denominador inteiros. Conjuntos Numéricos…
- 22. Prof. Bruno BastosNúmeros Racionais Números racionais são todos os números que podem ser escritos sob a forma de uma fracção com numerador e denominador inteiros. Conjuntos Numéricos…
- 23. Prof. Bruno BastosNúmeros Racionais Números racionais são todos os números que podem ser escritos sob a forma de uma fracção com numerador e denominador inteiros. Conjuntos Numéricos…
- 24. Prof. Bruno BastosNúmeros Racionais Números racionais são todos os números que podem ser escritos sob a forma de uma fracção com numerador e denominador inteiros. Conjuntos Numéricos…
- 25. Prof. Bruno BastosNúmeros Racionais Números racionais são todos os números que podem ser escritos sob a forma de uma fracção com numerador e denominador inteiros. Conjuntos Numéricos…
- 26. Prof. Bruno BastosNúmeros Racionais Conjuntos Numéricos…
- 27. Prof. Bruno Bastoslê-se “um meio” Números Racionais Conjuntos Numéricos…
- 28. Prof. Bruno Bastoslê-se “um meio” Números Racionais lê-se “dois terços” Conjuntos Numéricos…
- 29. Prof. Bruno Bastoslê-se “um meio” Números Racionais lê-se “dois terços” lê-se “sete oitavos” Conjuntos Numéricos…
- 30. Prof. Bruno Bastoslê-se “um meio” Números Racionais lê-se “dois terços” lê-se “sete oitavos” lê-se “quatro treze avos” Conjuntos Numéricos…
- 31. Prof. Bruno BastosNúmeros Racionais Conjuntos Numéricos…
- 32. Prof. Bruno BastosNúmeros Racionais A representação matemática deste conjunto é: Conjuntos Numéricos…
- 33. Prof. Bruno BastosNúmeros Racionais A representação matemática deste conjunto é: Conjuntos Numéricos… = {números fraccionários relativos} Q Z
- 34. Prof. Bruno BastosConjuntos Numéricos… Números Racionais
- 35. Números Racionais ConjuntosNuméricos… Prof. Bruno Bastos e os subconjuntos de Q Q
- 36. Números Racionais ConjuntosNuméricos… Prof. Bruno Bastos e os subconjuntos de Q Q = {números fraccionários relativos} Q Z
- 37. Números Racionais ConjuntosNuméricos… Prof. Bruno Bastos = {números racionais positivos} Q + e os subconjuntos de Q Q = {números fraccionários relativos} Q Z
- 38. Números Racionais ConjuntosNuméricos… Prof. Bruno Bastos = {números racionais positivos} = {números racionais negativos} Q - Q + e os subconjuntos de Q Q = {números fraccionários relativos} Q Z
- 39. Números Racionais ConjuntosNuméricos… = {números racionais positivos} = {números racionais negativos} = {números racionais não negativos} Prof. Bruno Bastos Q - Q + Q + 0 e os subconjuntos de Q Q = {números fraccionários relativos} Q Z
- 40. Números Racionais ConjuntosNuméricos… = {números racionais positivos} = {números racionais negativos} = {números racionais não negativos} = {números racionais não positivos} Prof. Bruno Bastos Q - Q + Q + 0 Q - 0 e os subconjuntos de Q Q = {números fraccionários relativos} Q Z
- 41. Prof. Bruno BastosNúmeros Racionais Conjuntos Numéricos…
- 42. Prof. Bruno BastosNúmeros Racionais Imagina que a seguinte figura é dividida em partes iguais . Conjuntos Numéricos…
- 43. Prof. Bruno BastosNúmeros Racionais Se dividirmos a figura em 2 partes iguais temos… Conjuntos Numéricos…
- 44. Prof. Bruno BastosNúmeros Racionais Conjuntos Numéricos…
- 45. Prof. Bruno BastosNúmeros Racionais Conjuntos Numéricos…
- 46. Prof. Bruno BastosNúmeros Racionais Cada uma das partes vale… Conjuntos Numéricos…
- 47. Prof. Bruno BastosNúmeros Racionais Cada uma das partes vale… Conjuntos Numéricos…
- 48. Prof. Bruno BastosNúmeros Racionais = Conjuntos Numéricos…
- 49. Prof. Bruno BastosNúmeros Racionais Se dividirmos a figura em 4 partes iguais temos… Conjuntos Numéricos…
- 50. Prof. Bruno BastosNúmeros Racionais Conjuntos Numéricos…
- 51. Prof. Bruno BastosNúmeros Racionais Conjuntos Numéricos…
- 52. Prof. Bruno BastosNúmeros Racionais Cada uma das partes vale… Conjuntos Numéricos…
- 53. Prof. Bruno BastosNúmeros Racionais Cada uma das partes vale… Conjuntos Numéricos…
- 54. Prof. Bruno BastosNúmeros Racionais = Conjuntos Numéricos…
- 55. Prof. Bruno BastosNúmeros Racionais Se dividirmos a figura em 9 partes iguais temos… Conjuntos Numéricos…
- 56. Prof. Bruno BastosNúmeros Racionais Conjuntos Numéricos…
- 57. Prof. Bruno BastosNúmeros Racionais Conjuntos Numéricos…
- 58. Prof. Bruno BastosNúmeros Racionais Cada uma das partes vale… Conjuntos Numéricos…
- 59. Prof. Bruno BastosNúmeros Racionais Cada uma das partes vale… Conjuntos Numéricos…
- 60. Prof. Bruno BastosNúmeros Racionais = Conjuntos Numéricos…
- 61. Prof. Bruno BastosConjuntos Numéricos…
- 62. Prof. Bruno BastosConjuntos Numéricos… Agora é fácil de entender que…
- 63. Prof. Bruno BastosConjuntos Numéricos… … se tivermos uma figura…
- 64. Prof. Bruno BastosConjuntos Numéricos… … e a dividirmos em 3 partes iguais…
- 65. Prof. Bruno BastosConjuntos Numéricos… … escolher uma dessas partes…
- 66. Prof. Bruno BastosConjuntos Numéricos… … é escolher um terço do total da figura, ou seja…
- 67. Prof. Bruno BastosConjuntos Numéricos… … o numerador indica o número de partes que se tem do todo… Numerador
- 68. Prof. Bruno BastosConjuntos Numéricos… … o denominador indica o número de partes iguais em que se dividiu o todo… Denominador
- 69. Prof. Bruno BastosConjuntos Numéricos… … tem-se então…
- 70. Prof. Bruno BastosConjuntos Numéricos… … tem-se então… um terço
- 71. Prof. Bruno BastosConjuntos Numéricos…
- 72. Prof. Bruno BastosConjuntos Numéricos… DIAGRAMA N
- 73. Prof. Bruno BastosConjuntos Numéricos… DIAGRAMA N 0 N
- 74. Prof. Bruno BastosConjuntos Numéricos… DIAGRAMA Z N 0 N
- 75. Prof. Bruno BastosConjuntos Numéricos… DIAGRAMA Q Z N 0 N
- 76. Conjuntos Numéricos… Prof.Bruno Bastos
- 77. Conjuntos Numéricos… Prof.Bruno Bastos Recordar…
- 78. Conjuntos Numéricos… Prof.Bruno Bastos Recordar… UTILIZA-SE ENTRE…
- 79. Conjuntos Numéricos… Prof.Bruno Bastos Recordar… UTILIZA-SE ENTRE… Um elemento e um conjunto Não pertence Pertence
- 80. Conjuntos Numéricos… Prof.Bruno Bastos Recordar… UTILIZA-SE ENTRE… Dois conjuntos Não está contido Está contido Um elemento e um conjunto Não pertence Pertence
- 81. Conjuntos Numéricos… Prof.Bruno Bastos Recordar… UTILIZA-SE ENTRE… Dois conjuntos Intersecção Reunião Dois conjuntos Não está contido Está contido Um elemento e um conjunto Não pertence Pertence
- 82. Conjuntos Numéricos… Prof.Bruno Bastos Recordar… UTILIZA-SE ENTRE… Dois números Menor Maior Dois conjuntos Intersecção Reunião Dois conjuntos Não está contido Está contido Um elemento e um conjunto Não pertence Pertence
- 83. Conjuntos Numéricos… Prof.Bruno Bastos Recordar… UTILIZA-SE ENTRE… Dois números Menor ou igual Maior ou igual Dois números Menor Maior Dois conjuntos Intersecção Reunião Dois conjuntos Não está contido Está contido Um elemento e um conjunto Não pertence Pertence
- 84. Prof. Bruno BastosConjuntos Numéricos…
- 85. Prof. Bruno BastosCuriosidades… Conjuntos Numéricos…
- 86. Prof. Bruno BastosCuriosidades… é a abreviatura da palavra “Natural” Conjuntos Numéricos… N
- 87. Prof. Bruno BastosCuriosidades… é a abreviatura da palavra “Natural” da palavra alemã “Zahlen”, que significa números Conjuntos Numéricos… Z N
- 88. Prof. Bruno BastosCuriosidades… é a abreviatura da palavra “Natural” da palavra alemã “Zahlen”, que significa números da palavra “Quociente”. Conjuntos Numéricos… Q Z N
- 89. Prof. Bruno BastosCuriosidades… Conjuntos Numéricos…
- 90. Prof. Bruno BastosCuriosidades… Repara que a letra que representa um conjunto numérico tem um traço a mais do que a letra do alfabeto… Conjuntos Numéricos…
- 91. Prof. Bruno BastosCuriosidades… Repara que a letra que representa um conjunto numérico tem um traço a mais do que a letra do alfabeto… Letra do alfabeto O conjunto dos números naturais Conjuntos Numéricos… N N
- 92. Prof. Bruno BastosCuriosidades… Repara que a letra que representa um conjunto numérico tem um traço a mais do que a letra do alfabeto… … assim sabemos sempre quando nos estamos a referir a um conjunto de números e não à letra. Letra do alfabeto O conjunto dos números naturais Conjuntos Numéricos… N N
- 93. Prof. Bruno BastosOs Números… FIM