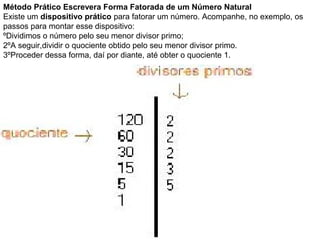
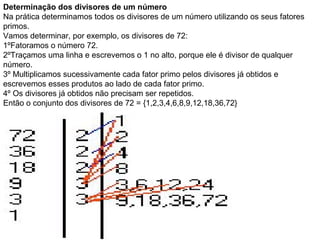
O documento discute conceitos matemáticos como múltiplos, divisores, números primos e suas propriedades. Também apresenta um jogo educacional sobre esses tópicos chamado "Borboletas" e discute como objetos de aprendizagem podem ser usados para construir conhecimento.

1. MÚLTIPLOS E DIVISORES
Aluna: Ane da Silva Oliveira Chagas
PÓLO: RIO BONITO

2. “Um Objeto de Aprendizagem é um arquivo digital
(imagem, filme, etc.) que pretende ser utilizado para
fins pedagógicos e que possui, internamente ou
através de associação, sugestões sobre o contexto
apropriado para sua utilização”. (Sosteric &
Hesemeier, 2001).

3. A IDEIA DE MÚLTIPLO E DIVISOR É CONHECIDA DESDE A
ANTIGÜIDADE GREGA. NAQUELA ÉPOCA, OS SÁBIOS DAVAM
TANTA IMPORTÂNCIA AOS NÚMEROS QUE LHES
ATRIBUÍAM CARACTERÍSTICAS HUMANAS. PARA VOCÊS
TEREM UMA IDEIA, ELES AGRUPAVAM OS NÚMEROS EM
MASCULINOS ( OS ÍMPARES) E FEMININOS ( OS PARES).
MÚLTIPLOS E DIVISORES

4. CRITÉRIOS DE MÚLTIPLOS E
DIVISORES
• Divisibilidade
Critérios de divisibilidade:
• São critérios que nos permite verificar se um número é divisível por
outro sem precisarmos efetuar grandes divisões.
• Um número natural é divisível por outro natural, excluindo-se o zero, se a
divisão entre eles é exata, ou seja, se tem resto zero.
• Divisibilidade por 2 Um número natural é divisível por 2 quando ele
termina em 0, ou 2, ou 4, ou 6, ou 8, ou seja, quando ele é par.
 Exemplos :
• 8490é divisível por 2, pois termina em 0.
• 895 não é divisível por 2, pois não é um número par

5. •Divisibilidade por 3 :Um número é divisível por 3 quando a soma dos valores absolutos dos
seus algarismos for divisível por 3.
Exemplo:
870 é divisível por 3, pois a soma de seus algarismos é igual a 8+7+0=15, como 15 é divisível
por 3, então 870 é divisível por 3.
•Divisibilidade por 4 :Um número é divisível por 4 quando termina em 00 ou quando o número
formado pelos dois últimos algarismos da direita for divisível por 4.
Exemplo:
9500 é divisível por 4, pois termina em 00.
6532 é divisível por 4, pois 32 é divisível por 4.
836 é divisível por 4, pois 36 é divisível por 4.
9870 não é divisível por 4, pois não termina em 00 e 70 não é divisível por 4.
•Divisibilidade por 5 Um número natural é divisível por 5 quando ele termina em 0 ou 5.
Exemplos:
425 é divisível por 5, pois termina em 5.
78960 é divisível por 5, pois termina em 0.
976 não é divisível por 5, pois não termina em 0 nem em 5.

6. •Divisibilidade por 6: Um número é divisível por 6 quando é divisível por 2 e por 3 ao mesmo
tempo.
Exemplos:
6456 é divisível por 6, porque é divisível por 2e por 3 ao mesmo tempo.
984 não é divisível por 6, é divisível por 2, mas não é divisível por 3.
357 não é divisível por 6, é divisível por 3, mas não é divisível por 2.
•Divisibilidade por 8: Um número é divisível por 8 quando termina em 000, ou quando o
número formado pelos três últimos algarismos da direita for divisível por 8.
Exemplos:
2000 é divisível por 8, pois termina em 000.
98120 é divisível por 8, pois 120 é divisível por 8.
78341 não é divisível por 8, pois 341 não é divisível por 8.
•Divisibilidade por 9: Um número é divisível por 9 quando a soma dos valores absolutos dos
seus algarismos for divisível por 9.
Exemplo:
6192 é divisível por 9, pois a soma de seus algarismos é igual a 6+1+9+2=18, e como 18 é
divisível por 9, então 6192 é divisível por 9.
Divisibilidade por 10 Um número natural é divisível por 10 quando ele termina em 0.
Exemplos:
8970 é divisível por 10, pois termina em 0.
5987 não é divisível por 10, pois não termina em 0.

7. MÚLTIPLOS
• Se um número é divisível por outro, diferente de zero, então
dizemos que ele é múltiplo desse outro.
• Os múltiplos de um número são calculados multiplicando-se esse
número pelos números naturais. Exemplo: os múltiplos de 7 são:
7x0 , 7x1, 7x2 , 7x3 , 7x4 , ... = 0 , 7 , 14 , 21 , 28 , ...
• ATENÇÃO:
• Observações importantes
1) Um número tem infinitos múltiplos
2) Zero é múltiplo de qualquer número natural

8. NÚMEROS PRIMOS
• Número primo: É quando um número só é divisível por dois números diferentes; 1 e
ele mesmo.
 Exemplos:
• 2 tem apenas os divisores 1e 2, portanto 2 é primo.
23 tem apenas os divisores 1e 23, portanto 23 é primo.
10 tem os divisores 1, 2, 5e 10, portanto 10 não é primo.
Atenção:
• 1 não é um número primo, porque ele tem apenas um divisor ele mesmo.
• 2 é o único número primo que é par.
• Os números que têm mais de dois divisores são chamados números compostos.
 Exemplo: 36 tem mais de dois divisores então 36 é um número composto.

9. Como saber se um número é primo
Devemos dividir o número dado pelos números primos menores que ele,
até obter um quociente menor ou igual ao divisor. Se nenhum das
divisões for exata, o número é primo.
Decomposição em fatores primos
Todo número natural, maior que 1, pode ser escrito na forma de uma
multiplicação em que todos os fatores são números primos. É o que nós
chamamos de forma fatorada de um número.
Decomposição do número 36:
36 =9 x 4
36 = 3 x 3 x 2 x 2
36 = 3 x3 x 2 x 2 = 22x32
No produto 2 x 2 x 3 x 3 todos os fatores são primos.
Chamamos de fatoração de 36 a decomposição de 36 num produto de
fatores primos.

10. Método Prático Escrevera Forma Fatorada de um Número Natural
Existe um dispositivo prático para fatorar um número. Acompanhe, no exemplo, os
passos para montar esse dispositivo:
ºDividimos o número pelo seu menor divisor primo;
2ºA seguir,dividir o quociente obtido pelo seu menor divisor primo.
3ºProceder dessa forma, daí por diante, até obter o quociente 1.

11. Determinação dos divisores de um número
Na prática determinamos todos os divisores de um número utilizando os seus fatores
primos.
Vamos determinar, por exemplo, os divisores de 72:
1ºFatoramos o número 72.
2ºTraçamos uma linha e escrevemos o 1 no alto, porque ele é divisor de qualquer
número.
3º Multiplicamos sucessivamente cada fator primo pelos divisores já obtidos e
escrevemos esses produtos ao lado de cada fator primo.
4º Os divisores já obtidos não precisam ser repetidos.
Então o conjunto dos divisores de 72 = {1,2,3,4,6,8,9,12,18,36,72}

12. Máximo Divisor Comum (mdc)
O máximo divisor comum entre dois ou mais números naturaisnão nulos (números
diferentes de zero) é o maior número queé divisor ao mesmo tempo de todos eles.
Não vamos aqui ensinar todos as formas de se calcular o mdc, vamos nos ater apenas
a algumas delas.
Regra das divisões sucessivas
Esta regra é bem prática para o calculo do mdc, observe:
Exemplo:
Vamos calcular o mdc entre os números 160 e 24.
1º: Dividimos o número maior pelo menor.
2º: Como não deu resto zero, dividimos o divisor pelo resto da divisão anterior.
3º: Prosseguimos com as divisões sucessivas até obter resto zero.
O mdc (64; 160) = 32

13. mmc (18, 25, 30) = 720
1º: Escrevemos os números
dados, separados por vírgulas, e
colocamos um traço vertical a
direita dos números dados.
2º: Abaixo de cada número
divisível pelo fator primo
colocamos o resultado da divisão.
O números não divisíveis pelo
fator primo são repetidos.
3º: Continuamos a divisão até
obtermos resto 1 para todos os
números.
Mínimo Múltiplo Comum - MMC

14. Objeto Aprendizagem - JOGOS
Os jogos quando convenientemente planejados, são um recurso
pedagógico eficaz para a construção do conhecimento matemático. Para
que o jogo seja um material produtivo em sala, o professor deve ter
alguns cuidados ao escolher os jogos a serem aplicados como:
•não tomar o jogo algo obrigatório;
•escolher jogos em que o fator sorte não interfira nas jogadas,
permitindo que vença aquele que descobrir as melhores estratégias;
•estabelecer regras;
• estudar o jogo antes de aplicá-lo ou seja jogá-lo antes.

15. O JOGO
•BORBOLETAS
•ANIMAÇÃO

16. O JOGO
Apanhar as borboletas que carregam os números
certos, no mais curto espaço de tempo. Cada jogo é
constituído por 3 fases (números primos, divisores,
etc...). Sempre que se apanha uma borboleta
errada será sujeito a uma penalização de 30
segundos.

18. COMO JOGAR

26. Os Números
•O Objetivo do jogo é descobrir as regras
de divisibilidade, múltiplos e seus
padrões usando rapidez e a lógica
através instrumentos educacionais , ou
seja, saber se um número é múltiplo ou
divisível por outro sem efetuar
multiplicação.
•Verificar os números primos.
•Identificar números pares.

27. CONCLUSÃO
Um objeto de aprendizagem é qualquer recurso que possa ser reutilizado para dar suporte
ao aprendizado. Sua principal idéia é "quebrar" o conteúdo educacional disciplinar em
pequenos trechos que podem ser reutilizados em vários ambientes de aprendizagem.
Qualquer material eletrônico que provém informações para a construção de conhecimento
pode ser considerado um objeto de aprendizagem, seja essa informação em forma de uma
imagem, uma página HTM, uma animação ou simulação.
RIVED - REDE INTERNACIONAL VIRTUAL DE EDUCAÇÃO

28. LINK
http://nautilus.fis.uc.pt/mn/p_index.html