Este documento apresenta notas de aulas de matemática ministradas pelo professor Joselias. As notas cobrem tópicos como números inteiros, fracionários, decimais, primos, divisibilidade e decomposição em fatores primos. As informações de contato do professor também são fornecidas.









![NOTAS DE AULAS - Matemática - Prof. Joselias
joselias@uol.com.br - www.concurseiros.org
e)1/525
Resposta: E
11) Efetue:
1 2 ⎡ 2 ⎛ 4⎞⎤
− ⋅ ⎢2 + ÷ ⎜ − ⎟ ⎥
30 5 ⎣ 3 ⎝ 5⎠⎦
a) -1/30
b) -2/30
c) -2/25
d) 2/35
e) N.R.A.
Resposta: E
12) Efetue:
⎛ 5 ⎞ ⎡⎛ 2 ⎞ ⎛ 2 ⎞ 4 ⎤
1− ⎜ − ⎟ ÷ ⎢⎜ − ⎟ ⋅ ⎜ − ⎟ ÷
⎝ 7 ⎠ ⎣⎝ 5 ⎠ ⎝ 3 ⎠ 25 ⎥ ⎦
a) 10/3
b) 10/7
c) 5/3
d) 5/7
e) N.R.A.
Resposta: B
13) Efetue:
2 ⎛ 3⎞
− 7⋅⎜− ⎟
3 ⎝ 5⎠
3 2 2
− ÷
4 5 15
a) –3/7
b) 35/7
c) –7/9
d) –911
e) N.R.A.
Resposta: E
14) Efetue:
[ ( −2 ) ]
7 5
÷ ( −2)
30
a) 64
b) 32
NOTAS DE AULAS- Matemática - Prof. Joselias 10
joselias@uol.com.br - www.concurseiros.org](https://image.slidesharecdn.com/apostilamatematicaeraciociniologicoconcursosexerciciosresolvidos-111008155627-phpapp02/85/RACIOCINIO-LOGICO-PARTE-03-10-320.jpg)

















































![NOTAS DE AULAS - Matemática - Prof. Joselias
joselias@uol.com.br - www.concurseiros.org
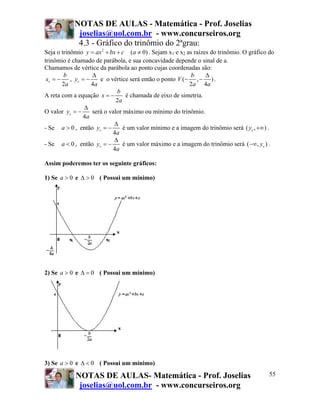
165) Um capital de R$ 25.000,00 foi aplicado durante 3 meses,
produzindo um montante de R$ 27.350,00. Qual a taxa trimestral dessa
aplicação?
Resposta: 9,4%
6.6 - Fator(ou Coeficiente) de Acumulação
Vimos no item anterior que a variação percentual é dada por:
Vnovo V
Δ= − 1 ⇒ novo = 1 + Δ ⇒ Vnovo = Vant [1 + Δ ]
Vant Vant
Vnovo
e Vant =
1+ Δ
O fator ou coeficiente de acumulação denotado por 1 + Δ, é o valor que
multiplicado pelo valor antigo produz o valor novo.
Notamos que para varias taxas de variação percentual consecutiva Δ1 , Δ2 , ... Δn
aplicadas sucessivamente obtemos a fórmula:
Vnovo = Vant (1+ Δ1)(1+ Δ2) ... (1+ Δn)
que será chamado de fator de acumulação total dos n períodos consecutivos. Temos
portanto que:
Δ = (1+ Δ1)(1+ Δ2) ... (1+ Δn) – 1
será chamada de taxa de variação total dos n períodos consecutivos.
Observação: Se Δ1 = Δ2 = ... = Δn = Δ a fórmula será Vnovo = Vant [1+ Δ]n
Exercícios:
166) Um comerciante comprou um artigo por R$ 200,00 e o vendeu por R$ 250,00.
Então o lucro sobre o preço de custo foi de:
a) 15%
b) 20%
c) 25%
d) 28%
e) 30%
Resposta: C
167) Um comerciante comprou um artigo por R$ 200,00 e o vendeu por R$ 250,00.
Então o lucro sobre o preço de venda foi de:
a) 15%
b) 20%
c) 25%
d) 28%
e) 30%
Resposta: B
NOTAS DE AULAS- Matemática - Prof. Joselias 62
joselias@uol.com.br - www.concurseiros.org](https://image.slidesharecdn.com/apostilamatematicaeraciociniologicoconcursosexerciciosresolvidos-111008155627-phpapp02/85/RACIOCINIO-LOGICO-PARTE-03-62-320.jpg)



















































![NOTAS DE AULAS - Matemática - Prof. Joselias
joselias@uol.com.br - www.concurseiros.org
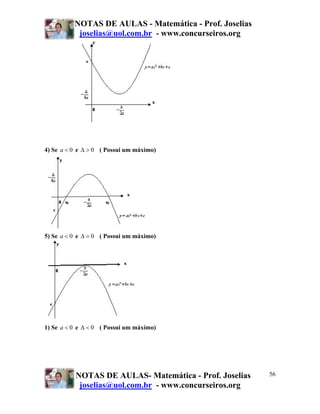
2 21 73 73
+
3 5 = 15 = 15 = − 73 x 4 = − 292
3 2 15 3 9 15 9 135
− . −3 −
4 5 2 4 4
Resp. e
14- Efetue:
[( −2) 7 ÷ ( −2) 30]
5
Solução:
( −2 ) ÷ ( −2 ) = ( −2 ) ÷ ( −2 ) = −32
7 x5 30 35 30
Resp. e
15- Qual a razão entre 0,4555... e 82/45 ?
Solução:
0, 4555 41 45 1
= . =
82 / 45 90 82 4
Resp. d
16) Efetue:
(2 ) ÷ (2 )
3
2
⋅ 32 4
⋅ 34
Solução:
( 2 ) .(3 )
2 3 2 3
=
26.36
= 22.32 = 4.9 = 36
( 2 ) .(3 )
4 4 4 4
2 .3
Resp. b
17) Efetue:
( −3) 5 ⋅ ( −3) 7 ⋅ ( −3)12 ÷ ( −3) 20
Solução:
( −3) ÷ ( −3 ) = ( − 3 ) ÷ ( − 3 ) = ( −3) = 81
5+ 7 +12 20 24 20 4
Resp. e
18) Efetue:
3 −2
4
2 −3
7
Solução:
NOTAS DE AULAS- Matemática - Prof. Joselias 114
joselias@uol.com.br - www.concurseiros.org](https://image.slidesharecdn.com/apostilamatematicaeraciociniologicoconcursosexerciciosresolvidos-111008155627-phpapp02/85/RACIOCINIO-LOGICO-PARTE-03-114-320.jpg)































































![NOTAS DE AULAS - Matemática - Prof. Joselias
joselias@uol.com.br - www.concurseiros.org
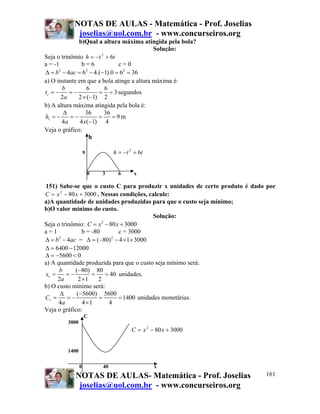
196) Calcular a taxa de juros simples aplicada a um capital de R$
4.000,00, durante 3 anos, sabendo-se que se um capital de R$ 10.000,00 fosse
aplicado durante o mesmo tempo, a taxa de juros simples de 5% a.a., renderia
mais R$ 600,00 que o primeiro.
Solução:
Observe que temos duas aplicações.
Primeira aplicação:
C = 4.000,00
n = 3 anos
J = R$ 900,00
I=?
Segunda aplicação:
C = 10.000,00
n =3 anos
J = R$ 600,00 a mais que o anterior
i = 5% a.a
J= C. i. n
J= 10.000x5%x3
J= 10.000x0,5x3
J= 1.500
J= R$ 1.500,00 – R$ 600,00 = R$ 900,00 (juros anterior)
Voltando a primeira aplicação temos:
J= C. i. n
900= 4.000 . i . 3
900 = 12000.i
i = 900/12000
i= 0,075 (Forma unitária)
i= 7,5% a.a
197) Duas pessoas fizeram aplicações de dinheiro na mesma data. Uma aplicou
R$192.000,00 a taxa de juros simples de 25% a.a. e a outra aplicou R$240.000,00 a
taxa de juros simples de 15% a.a.. Após quanto tempo os montantes das aplicações
serão iguais?
Solução:
A= 192.000,00 i = 25% a. a
B= 240.000,00 i =15% a.a
C= 192.000,00 C= 240.000,00
i= 25% a.a. i= 15% a.a.
n=? n=?
M= C. [1+1.n] M= C. [1+1.n]
M= 192.000 . [1+25%.n] M= 240.000 . [1+15%.n]
192.000 . (1+25% .n) = 240.000 . (1+ 15% .n)
192 . (1+25% .n) = 240 . (1+ 15% .n)
192 + 192 . 25% .n = 240 + 240. 15% .n
NOTAS DE AULAS- Matemática - Prof. Joselias 179
joselias@uol.com.br - www.concurseiros.org](https://image.slidesharecdn.com/apostilamatematicaeraciociniologicoconcursosexerciciosresolvidos-111008155627-phpapp02/85/RACIOCINIO-LOGICO-PARTE-03-179-320.jpg)



