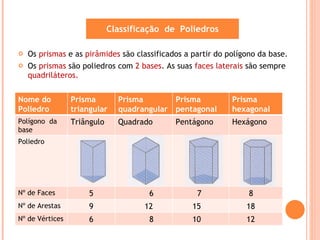
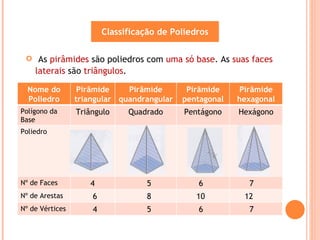
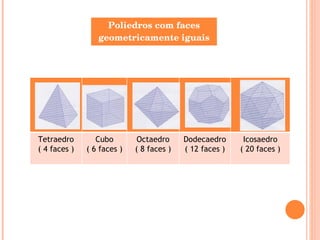
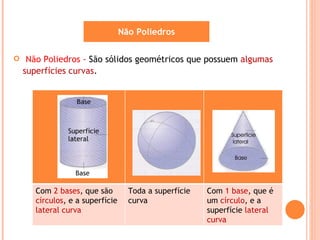
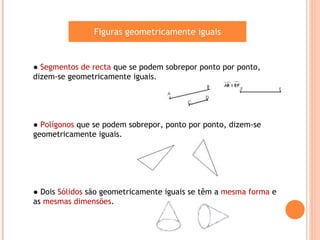
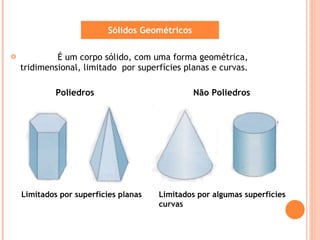
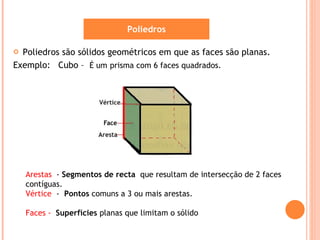
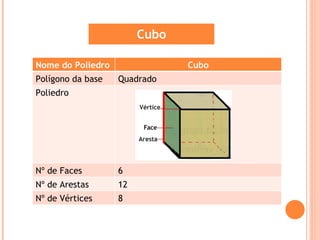
Este documento descreve diferentes tipos de sólidos geométricos, incluindo poliedros e não poliedros. Poliedros são sólidos com faces planas, como cubos e prismas. Não poliedros têm superfícies curvas. O documento fornece exemplos de vários poliedros com suas características e fórmulas para calcular vértices, arestas e faces.

1. SÓLIDOS GEOMÉTRICOS Poliedros e não poliédricos

2. Todos os seres vivos e não vivos, que nos rodeiam, têm formas geométricas próprias. As Formas existentes na Natureza e os Sólidos Geométricos Sólidos Geométricos Cubo Prisma Pirâmide Podemos associar a forma do cristal de pirite ao cubo e a forma do cristal de quartzo a um prisma hexagonal que termina em pirâmide hexagonal.

3. É um corpo sólido, com uma forma geométrica, tridimensional, limitado por superfícies planas e curvas. Sólidos Geométricos Limitados por superfícies planas Limitados por algumas superfícies curvas Poliedros Não Poliedros

4. Poliedros são sólidos geométricos em que as faces são planas. Exemplo: Cubo – É um prisma com 6 faces quadrados. Poliedros Arestas - Segmentos de recta que resultam de intersecção de 2 faces contíguas. Vértice - Pontos comuns a 3 ou mais arestas. Faces - Superfícies planas que limitam o sólido

5. Cubo Nome do Poliedro Cubo Polígono da base Quadrado Poliedro Nº de Faces 6 Nº de Arestas 12 Nº de Vértices 8

6. Polígonos – As figuras planas, que limitam os poliedros, denominam – se polígonos . Classificação de acordo com o nº de lados: Polígonos Polígono Regular: Quando os lados têm o mesmo comprimento e os ângulos a mesma amplitude Nome Triângulo Quadrilátero Pentágono Hexágono Polígono Nº de Lados 3 4 5 6

7. Recta, Semi-recta, Segmento de Recta O polígono da figura é o triângulo [ A B C] ● A, B, C, são vértices deste polígono ● [ AB] , [ BC] , [CA] são lados deste polígono, segmentos de recta. ● Prolongando para ambos os lados, indefinidamente o lado [ AC] , obtemos a recta r ou recta AC . ● Prolongando para um dos lados, indefinidamente o lado [ AB] , obtemos a semi-recta AB . ou AB ( semi-recta com origem em A ) ●

8. Os prismas e as pirâmides são classificados a partir do polígono da base. Os prismas são poliedros com 2 bases . As suas faces laterais são sempre quadriláteros. Classificação de Poliedros Nome do Poliedro Prisma triangular Prisma quadrangular Prisma pentagonal Prisma hexagonal Polígono da base Triângulo Quadrado Pentágono Hexágono Poliedro Nº de Faces 5 6 7 8 Nº de Arestas 9 12 15 18 Nº de Vértices 6 8 10 12

9. As pirâmides são poliedros com uma só base . As suas faces laterais são triângulos . Classificação de Poliedros Nome do Poliedro Pirâmide triangular Pirâmide quandrangular Pirâmide pentagonal Pirâmide hexagonal Polígono da Base Triângulo Quadrado Pentágono Hexágono Poliedro Nº de Faces 4 5 6 7 Nº de Arestas 6 8 10 12 Nº de Vértices 4 5 6 7

10. Fórmula Em qualquer poliedro: Nº de Faces + Nº de Vértices = Nº de Arestas + 2

11. Poliedros com faces geometricamente iguais Tetraedro ( 4 faces ) Cubo ( 6 faces ) Octaedro ( 8 faces ) Dodecaedro ( 12 faces ) Icosaedro ( 20 faces )

12. Não Poliedros - São sólidos geométricos que possuem algumas superfícies curvas . Não Poliedros Com 2 bases , que são círculos , e a superfície lateral curva Toda a superfície curva Com 1 base , que é um círculo , e a superfície lateral curva

13. Figuras geometricamente iguais ● Segmentos de recta que se podem sobrepor ponto por ponto, dizem-se geometricamente iguais. ● Polígonos que se podem sobrepor, ponto por ponto, dizem-se geometricamente iguais. ● Dois Sólidos são geometricamente iguais se têm a mesma forma e as mesmas dimensões .