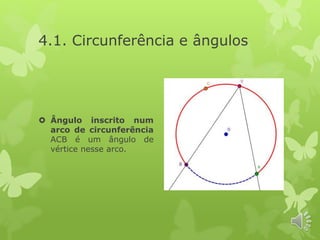
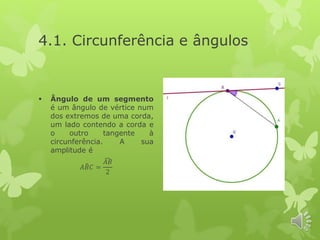
O documento discute conceitos geométricos relacionados a circunferências e polígonos. Ele explica que arcos e cordas determinados por ângulos iguais ao centro são iguais, e que retas contendo o centro de uma circunferência são perpendiculares às cordas. Também define vários tipos de ângulos relacionados a arcos de circunferência e discute propriedades dos ângulos internos e externos de polígonos convexos.

1. 4. Circunferência
4.1. Circunferência e ângulos
4.2. Polígonos

2. 4.1. Circunferência e ângulos
 Na figura ao lado estão
representados dois ângulos ao
centro, o ângulo côncavo BOA e o
ângulo convexo AOB, que, ao
intersetarem a circunferência,
definem dois arcos: o arco maior
AB (ou ACB) e o arco menor
BA.

3. 4.1. Circunferência e ângulos
À corda [CA] podemos associar-
lhe dois arcos, denominados
arcos subtensos pela corda
[CA]. O arco menor AC designa-
se por arco correspondente à
corda [AC].

4. 4.1. Circunferência e ângulos
Numa circunferência:
 Ou em circunferências iguais,
cordas e arcos determinados
por ângulos ao centro iguais
também são iguais e vice-
versa.

5. 4.1. Circunferência e ângulos
Numa circunferência:
 São iguais arcos
(respetivamente cordas)
determinados por duas retas
paralelas e compreendidos
entre elas.
r//s

6. 4.1. Circunferência e ângulos
Numa circunferência:
 Qualquer reta que contenha o
seu centro é perpendicular a
uma corda, bissetando-a,
assim como aos arcos
subtensos e aos ângulos ao
centro correspondentes.
r ꓕ [AB]
𝐴𝑀 = 𝑀𝐵 e 𝐵𝐶 = 𝐶𝐴
𝐶 𝑂𝐴 = 𝐵 𝑂𝐶

7. 4.1. Circunferência e ângulos
Numa circunferência:
 Uma reta que lhe é tangente é
perpendicular à reta que contém
o centro e o ponto de tangência.

8. 4.1. Circunferência e ângulos
 Ângulo inscrito num
arco de circunferência
ACB é um ângulo de
vértice nesse arco.

9. 4.1. Circunferência e ângulos
 A amplitude de um ângulo
inscrito é
B 𝑉𝐴 =
𝐵𝐴
2
 Ângulos inscritos no mesmo arco
de circunferência têm a mesma
amplitude.
 Qualquer ângulo inscrito numa
semicircunferência é reto.

10. 4.1. Circunferência e ângulos
 Ângulo de um segmento
é um ângulo de vértice num
dos extremos de uma corda,
um lado contendo a corda e
o outro tangente à
circunferência. A sua
amplitude é
𝐴 𝐵𝐶 =
𝐴𝐵
2

11. 4.1. Circunferência e ângulos
 Ângulo ex-inscrito num
arco de circunferência é
um ângulo adjacente a um
ângulo inscrito e a ele
suplementar. A sua
amplitude é
𝐵 𝑉𝐷 =
𝐴𝑉 + 𝑉𝐵
2

12. 4.1. Circunferência e ângulos
 Ângulo convexo com
vértice no interior de
um círculo, e
𝐶 𝑉𝐷 =
𝐶𝐷 + 𝐴
2

13. 4.1. Circunferência e ângulos
 Ângulo de vértice
exterior a um círculo,
cujos lados o intersetam,
e
𝐴 𝑉𝐷 =
𝐴𝐷 − 𝐵𝐶
2

14. 4.2. Polígonos
Ângulos de um polígono convexo:
Em qualquer polígono de n lados, tem-se que:
 A soma das medidas das amplitudes dos seus
ângulos internos é igual a 𝑛 − 2 × 180°.
Num polígono regular, a amplitude de cada ângulo
interno é igual a 180° −
360°
𝑛
;
 Cada ângulo interno e o ângulo externo que lhe é
adjacente são suplementares;

15. 4.2. Polígonos
 A soma das amplitudes dos ângulos externos é 360°.
Num polígono regular, a amplitude de cada ângulo
externo é igual a
360°
𝑛
.
Polígonos inscritos numa circunferência
Num quadrilátero inscrito numa circunferência, a soma das
amplitudes dos ângulos opostos é igual a um ângulo
raso (180°).