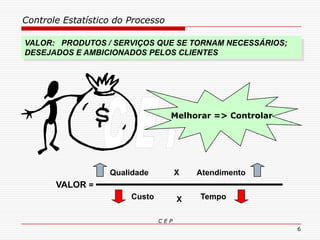
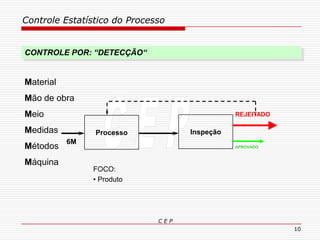
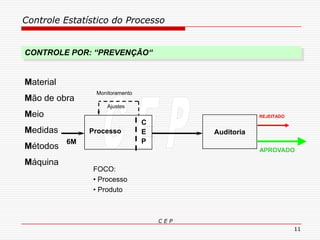
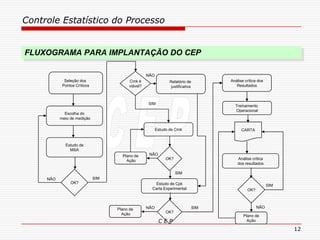
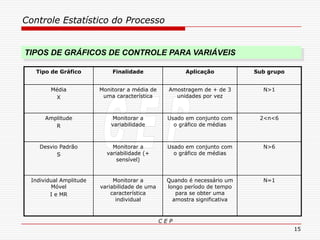
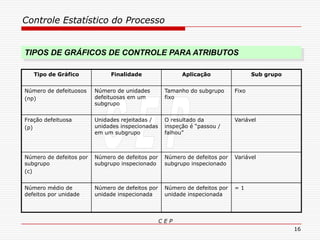
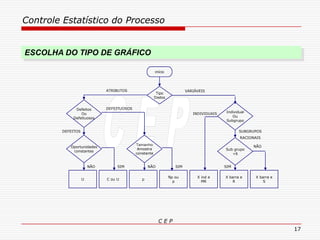
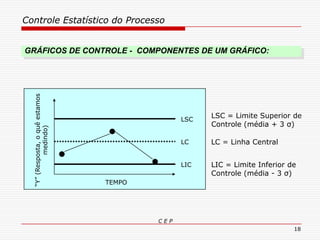
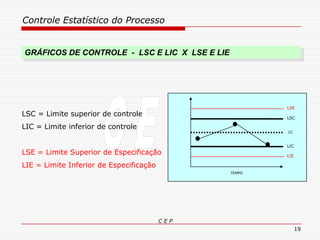
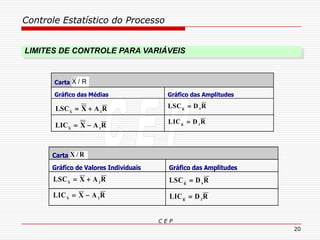
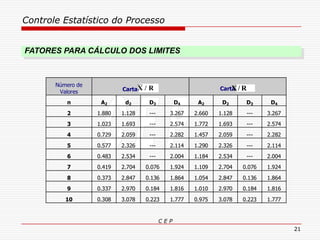
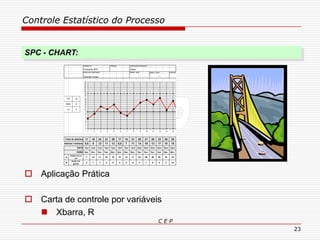
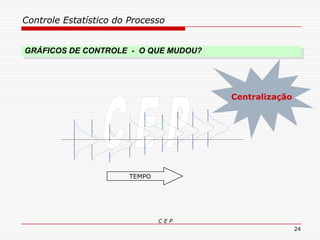
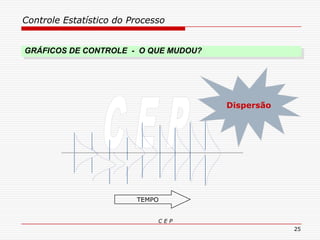
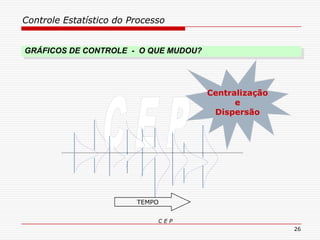
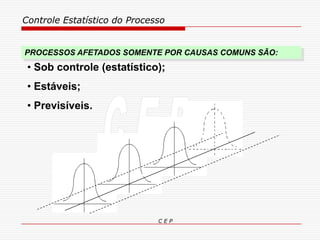
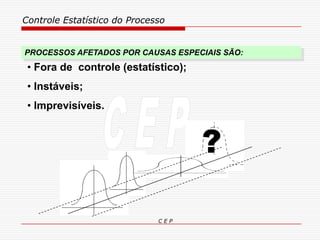
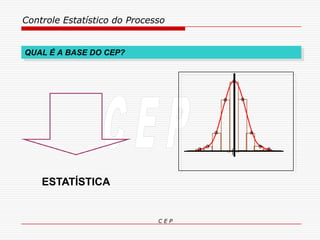
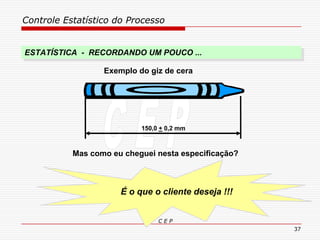
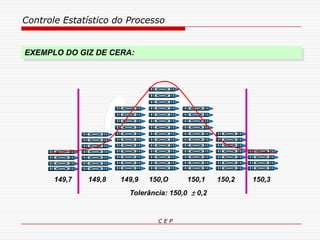
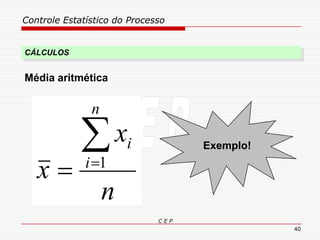
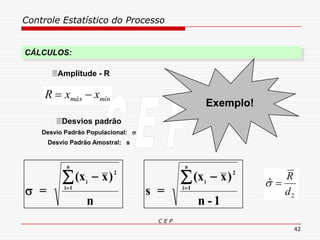
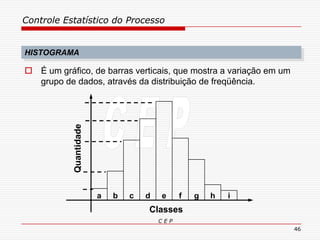
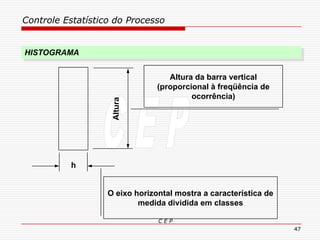
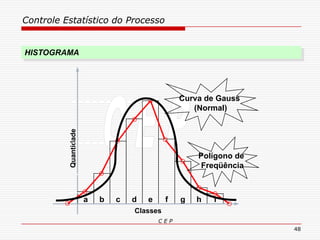
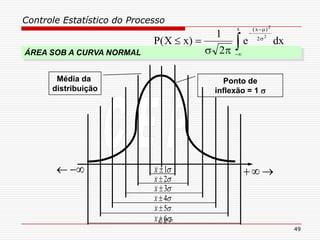
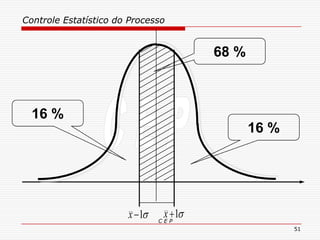
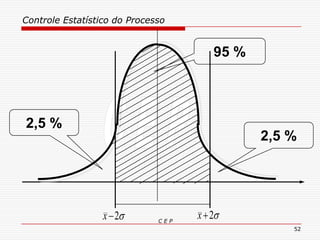
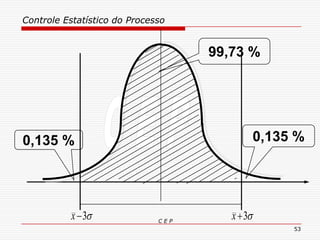
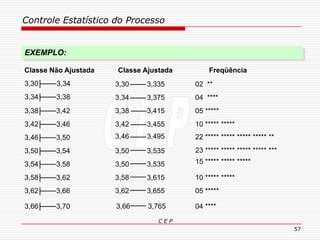
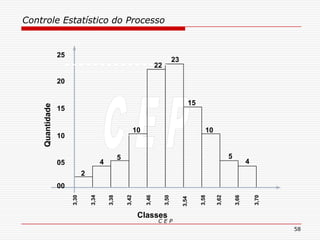
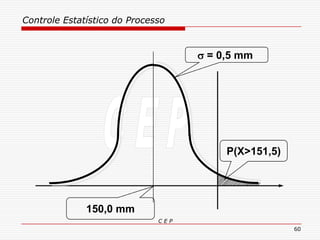
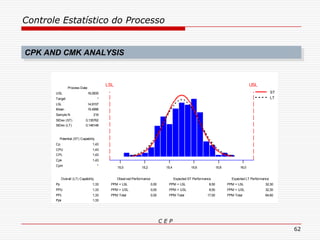
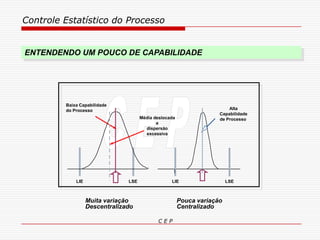
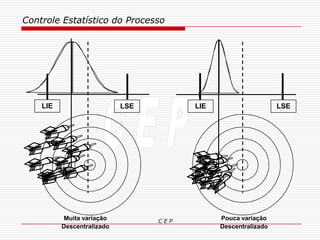
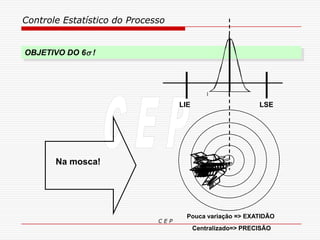
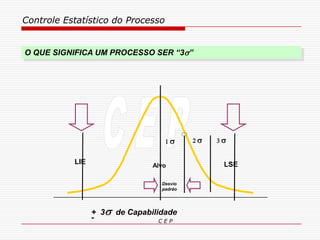
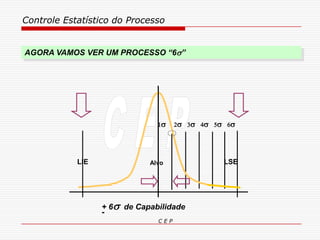
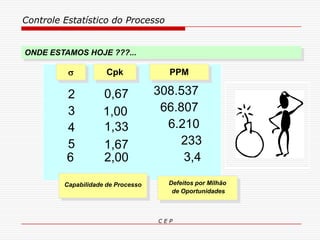
O documento discute os conceitos e aplicações do Controle Estatístico de Processo (CEP). Aborda os tipos de empresas, objetivos de uma empresa honesta, sobrevivência da empresa, valor para o cliente, formas de controle, tipos de gráficos de controle, limites de controle, detectando falta de controle e causas de variação em processos.