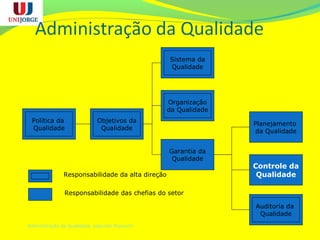
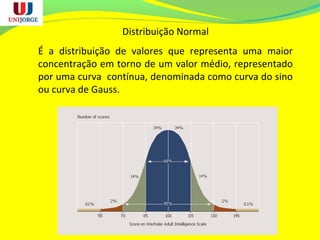
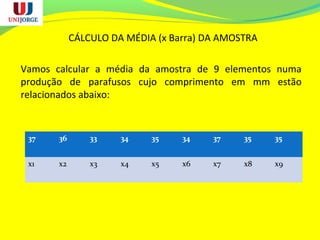
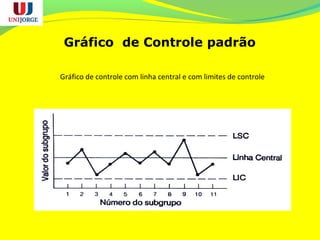
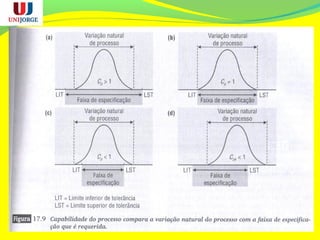
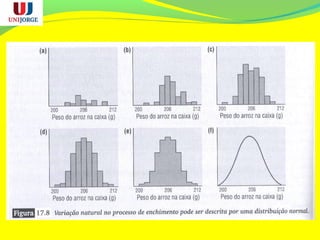
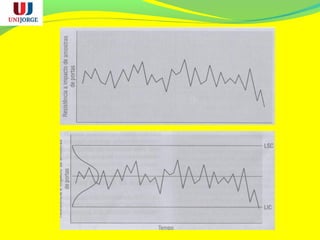
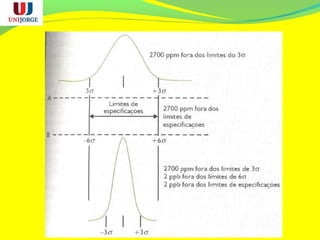
O documento discute os conceitos de controle estatístico de processo (CEP) e qualidade. O CEP envolve a coleta de dados estatísticos de amostras para monitorar processos de produção e identificar variações significativas que precisam ser eliminadas. O documento explica termos como média, desvio padrão e gráficos de controle usados no CEP para manter a qualidade dentro dos padrões especificados.

1. Curso: Eng da Produção

2. AULA 1

3. SUMÁRIO
A Administração da Qualidade
O Controle da Qualidade
CEP – Origem e história
Outros conceitos relacionados ao CEP
Média
Exercícios

4. Política da
Qualidade
Objetivos da
Qualidade
Sistema da
Qualidade
Organização
da Qualidade
Garantia da
Qualidade
Controle da
Qualidade
Planejamento
da Qualidade
Auditoria da
Qualidade
Responsabilidade da alta direção
Responsabilidade das chefias do setor
Administração da Qualidade, segundo Miyauchi

5. “Não se gerencia o que não se mede, não se
mede o que não se define, não se define o que
não se entende, não há sucesso no que não se
gerencia.”
Deming

6. Controle de Qualidade
- Estabelecer padrões de qualidade
- Checar se produtos e serviços estão conforme o padrão;
- Onde checar?
- Checar cada produto ou amostra?
- Como checar?

7. Onde checar?
- Identificar pontos de controle críticos.
- Início do processo (recebimento matéria prima);
- Durante o processo
- antes de uma série de processos (checagem difícil);
- depois do processo com alta taxa de falhas;
- antes de processo que possa esconder defeitos;
- antes de um “ponto sem volta”;
-antes de uma mudança de responsabilidade funcional.
- Depois do processo

8. Checar cada produto e serviço ou usar uma amostra*?
Perigo na checagem da amostra total;
- Checagem total pode destruir a amostra ou interferir no
serviço;
- Consumo excessivo de tempo para checagem total.
*Amostra (n) é o conjunto de elementos extraídos de uma
população aleatoriamente. Ex: um conjunto de parafusos
retirados de uma caixa.
** Amostragem (N) é o número de amostras consideradas para
um estudo. Ex: 5 grupos de 30 elementos cada
N=5 x 30 (n) = 150

9. Como as checagens devem ser feitas?
- Amostragem:
- CEP (Controle Estatístico do Processo)

10. O Controle Estatístico da Qualidade se faz através de uma das
ferramentas da Qualidade que chamamos de CEP – Controle
Estatístico do Processo e de algumas outras ferramentas
como folhas de verificação, gráficos de controle e
histogramas.

11. Origem
Bell Telephone e
Western Electric (~1930)
Necessidade: Aprimorar a
uniformidade de peças
manufaturadas em uma
linha de produção.
Walter Andrew Shewhart
Cartas de Controle

12. Após 1944
EUA – Europa e Japão (produção em larga escala)
Método:
Eficiente: Matemática aplicada
Seguro: Aplicado no dia-a-dia
Rápido: pequenas amostras

13. Correção x Prevenção
Custos da Produção
(qualidade / produtividade / competitividade)

14. Conceitos:
Controle: manter algo dentro dos limites (padrões/especificações)
ou fazer algo se comportar de maneira adequada.
Estatística: obter conclusões com base em dados e números
Processo: é a combinação necessária entre o homem, e os recursos
disponívies para fabricar um produto qualquer. Mais
especificamente um processo é um conjunto de operações
simultâneas, utilizando os recursos disponíveis, para produzir um
determinado resultado.

15. Controle Estatístico do Processo é então…
Um método preventivo de se comparar continuamente, os
resultados de um processo com os padrões/especificações
identificados, a partir de dados estatísticos, as tendências para
variações significativas, a fim de eliminar/controlar essas variações,
com o objetivo de reduzí-las cada vez mais.

16. CEP – Controle Estatístico do Processo
(SPC – Statistical Process Control)
- Checagem do produto ou serviço durante o processo;
- Evita eliminação de lotes defeituosos;
- Gráficos de controle;
- Desvios corrigidos antes que haja problema;
- Investigação de tendências.

17. CEP – Controle Estatístico do Processo
Variação na qualidade de processo:
- Todos os processos variam em alguma medida;
- Máquina
- Operador
- Ambiente
- Variação pode ser reduzida, nunca eliminada.

18. AULA 2

19. CEP – Controle Estatístico do Processo
Conceitos e Tipos de Variações
Variações Aleatórias (comuns): Fazem parte da natureza do
processo, podem ser controladas e seguem padrões normais
de comportamento. Ex: uma usinagem dentro de uma
determinada medida.
Variações causais ( especiais): São de certa forma
imprevisíveis. Quando detectadas devem ser eliminadas
rapidamente para não prejudicarem o desempenho do
processo. Ex: Quebra de uma ferramenta de corte.

20. DEFINIÇÕES
ELEMENTO (x):
É a unidade considerada para o estudo estatístico.
Ex. objeto, peça, indivíduo, conjunto...
POPULAÇÃO:
É o conjunto de todos os elementos (ou itens) extraídos de uma
população. Ex. todos os veículos Gol, Ano/Modelo 2009,; todas
peças produzidas em um torno...

21. DEFINIÇÕES
AMOSTRA (n):
É o conjunto de elementos extraídos de uma população
aleatoriamente. Ex: um conjunto de parafusos retirados de uma
caixa.
TAMANHO DA AMOSTRA
É o número de elementos ( ou itens), existentes na amostra

22. DEFINIÇÕES
AMOSTRAGEM (N):
É o número de amostras consideradas para um estudo. Ex: 5 grupos de
30 elementos cada
N=5 x 30 (n) = 150
Tipos de amostragem
a)Instantânea: refere-se a amostragem composta de amostras, cujos
elementos foram obtidos num mesmo momento
Ex. 5 peças consecutivas produzidas por uma máquina
b) Periódica: refere-se às retiradas, durante um certo período, em
intervalos de tempo pré-estabelecidos. Tende a representar melhor o
tamanho da população.
Ex. 5 peças retiradas aleatoriamente a cada 5 horas

23. Distribuição Normal
É a distribuição de valores que representa uma maior
concentração em torno de um valor médio, representado
por uma curva contínua, denominada como curva do sino
ou curva de Gauss.

24. DEFINIÇÕES
DESVIO PADRÃO:
É a medida de dispersão em relação a média, identificada pela
letra grega sigma ( ou pela letra “s”).
DADOS MENSURÁVEIS:
São os que podem ser expressos em unidade básica de medidas.
Ex. kg, cm, ml...
DADOS ATRIBUTIVOS:
São os dados enumeráveis ou contáveis que estabelecem
presença ou ausência de um atributo.
Ex. número de peças defeituosas

25. DEFINIÇÕES
AMPLITUDE (R):
É a diferença entre o maior e o menor valor de uma amostra. É
uma medida de dispersão.
MÉDIA:
A Média aritmética simples é uma medida de posição.

26. CÁLCULO DA MÉDIA (x Barra) DA AMOSTRA
Vamos calcular a média da amostra de 9 elementos numa
produção de parafusos cujo comprimento em mm estão
relacionados abaixo:
37 36 33 34 35 34 37 35 35
x1 x2 x3 x4 x5 x6 x7 x8 x9

27. X = somatório de todos os elementos
número de elementos
X = 37+36+33+34+35+34+37+35+35
9
X = 35,1
CÁLCULO DA MÉDIA (x Barra) DA AMOSTRA

28. MEDIANA:
É o valor central ou o valor do meio de uma sequencia
crescente ou decrecente. É uma medida de projeção.
Ex.
37 36 33 34 35 34 37 35 35
x1 x2 x3 x4 x5 x6 x7 x8 x9
Passo 1 – Ordenar as amostras :
37, 37, 36, 35, 35, 35, 34,33
Passo – Determinar o elemento central: 35

29. EXERCÍCIOS
CALCULE A AMPLITUDE, A MÉDIA (x barra) E MEDIANA
DAS AMOSTRAS DA FOLHA DE EXERCÍCIOS

30. AULA 3

31. MAIS ALGUNS CONCEITOS...
DISCREPÂNCIA:
É o ponto de discordância de um elemento com relação a uma
dada característica da qualidade.
DEFEITO:
É uma discrepância de tal grau que torna uma unidade
inaceitável.
DEFEITUOSO:
É uma unidade que contém defeitos, ou seja, não atende aos
padrões requeridos, tornando toda unidade inaceitável. Um
defeituoso, pode, portanto, ter um ou mais defeitos.

32. MAIS ALGUNS CONCEITOS...
GRÁFICO DE CONTROLE:
É uma projeção gráfica, no tempo, do comportamento do
processo.
LIMITES DE CONTROLE:
São fronteiras da região onde estão compreendidas 99,74% das
variações aleatórias de um processo.
TOLERÂNCIA:
É o campo de variação permitida numa característica da
qualidade.

33. MAIS ALGUNS CONCEITOS...
LIMITES DE ESPECIFICAÇÃO:
São os limites de tolerância, dentro dos quais um processo pode
variar.
CAPACIDADE DO PROCESSO:
É a condição de produzir continuamente dentro das exigências.
ÍNDICE DE CAPACIDADE DO PROCESSO (Icp):
É um número obtido a partir da comparação da tolerância do
produto com a variação aleatória do processo.

34. Desvio Padrão (s)
É a medida de dispersão em relação a média.
É calculado da seguinte forma:
É a raiz quadrada da soma das médias dos desvios ao quadrado
VALOR DESVIO (X - xbarra) DESVIO2
(X - xbarra)2
35 1 1
34 0 0
33 -1 1
∑ 2
Xbarra = 34
S =√ ∑(x-xbarra)2
/ n-1 = √2/2 = 1

35. EXERCÍCIOS
CALCULE A AMPLITUDE, A MÉDIA (x barra) E MEDIANA E
O DESVIO PADRÃO DAS AMOSTRAS DA FOLHA DE
EXERCÍCIOS.

36. AULA 4

37. Desvio Padrão aproximado(Sx)
É calculado da seguinte forma:
a)Para amostras tamanho n<100 elementos.
R=Xmax – Xmin = 2
De acordo com a tabela Fator para Estimar o Desvio Padrão, para
3 amostras, d2=1,693
Sx= R/d2
Sx = 2/1,693
Sx = 1,18
b) Para amostras n>100 elementos: dividir em subgrupos

38. AULA 5

39. ÁREAS DE PROBABILIDADE SOB A CURVA NORMAL

40. Gráficos de Controle
 São empregados para evitar, reduzir ou eliminar não
conformidades em tempo real (durante o processo de
produção);
 Utiliza os dados de uma série de amostras pequenas
chamadas de “grupos racionais”, para estimar onde o processo
está centralizado e quanto ele está variando em torno desse
centro;
 Os parâmetros estatísticos a serem utilizados são a Média
Estimada e a Variabilidade do processo;

41. Gráficos de Controle
 Média do Processo: é um valor desconhecido estimado
pela média da amostra;
 Variação do Processo: todo o processo seja natural ou
artificial sofre variações;
 Variação Admissível: consiste no valor nominal do
parâmetro a ser controlado, mais ou menos a tolerância
aceitável.
Ex. Umidade = 4,0% + 0,2%;
- valor nominal: 4,0%; variação admissível: 3,8% a 4,2%

42. Gráfico de controle com linha central e com limites de controle
Gráfico de Controle padrão

43. CEP – Controle Estatístico do Processo
Capabilidade de Processo:
- Medida da aceitabilidade da variação do processo.
- Razão entre a faixa de especificação e a variação “natural” do
processo (± 3 desvios-padrão);
- Cp = LST – LIT
6s
Cp >1 = Processo capaz
Cp <1 = Processo não capaz

45. CEP – Controle Estatístico do Processo
Análise das variações
-Variação Natural?
- Sintoma de causa mais séria?
- Limites de Controle nos gráficos
- Pontos fora dos limites = processo fora de controle

48. CEP – Controle Estatístico do Processo
Qualidade Seis Sigmas
- Motorola
- Especificações mais apertadas
- 3σ = 99,73% dentro – 2,7 erros por 1000 peças
- 6σ = 99,99966% dentro – 2 erros por 1.000.000.000 peças