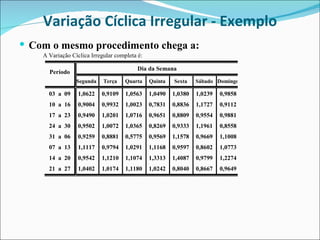
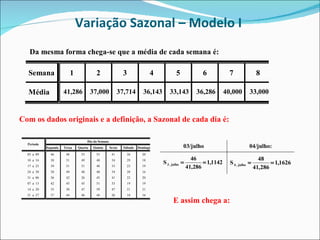
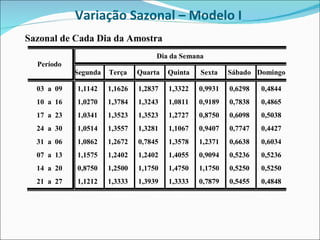
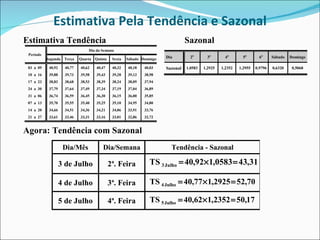
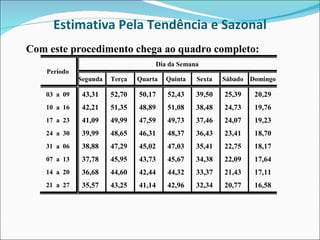
O documento descreve o modelo multiplicativo para séries temporais, incluindo: 1) Cada componente do modelo (tendência, sazonal, cíclica e irregular) é avaliado separadamente; 2) A variação sazonal é calculada como a porcentagem de cada período típico em relação ao período total; 3) A variação cíclica-irregular é obtida dividindo cada valor observado pela estimativa de tendência-sazonal.

1. Séries Temporais (Parte 3 - Modelo Multiplicativo) Prof. Gercino Monteiro Filho

9. Variação Sazonal – Modelo I