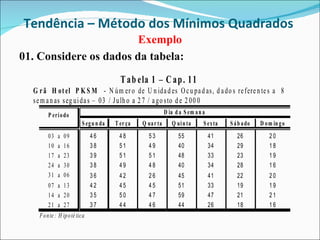
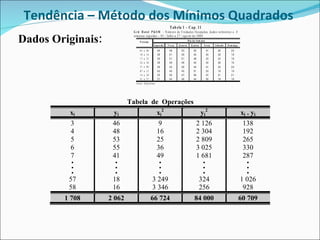
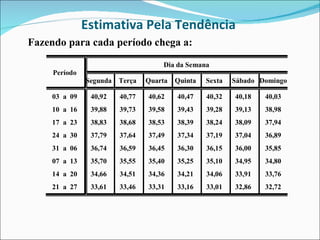
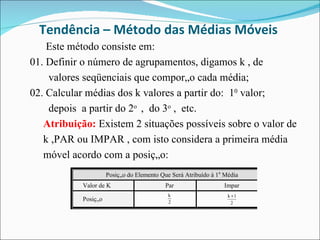
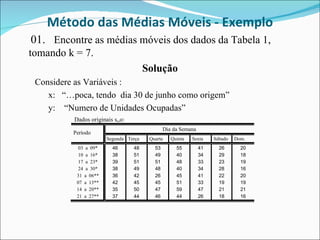
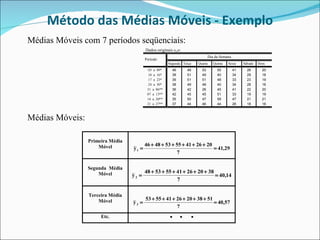
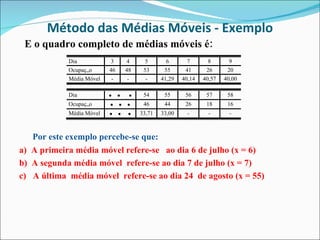
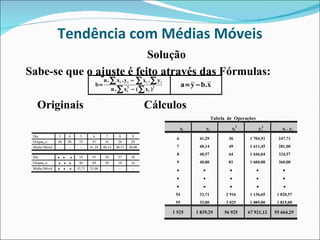
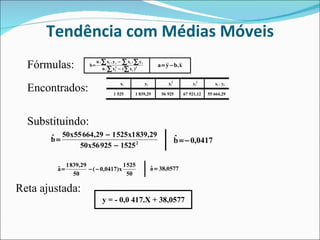
Este documento descreve dois métodos para encontrar a tendência em séries temporais: (1) Método dos mínimos quadrados, que ajusta uma curva matemática aos dados originais usando modelos de regressão; (2) Método das médias móveis, que calcula médias de conjuntos sequenciais de valores para suavizar os dados. O documento fornece um exemplo detalhado de como aplicar cada método a um conjunto de dados sobre ocupação hoteleira.

1. Séries Temporais (Parte 2 - Tendência) Prof. Gercino Monteiro Filho

2. Séries Temporais - Tendência Para encontrar a função que fornece o valor da tendência em cada tempo, usa um dos modelos: I. Método dos Mínimos Quadrados II . Método das médias móveis;

3. Tendência – Método dos Mínimos Quadrados Este Método consiste em ajustar uma curva aos dados originais conforme os modelos matemáticos já estudados no capítulo 10 , referente a Regressão e Correlação. O cuidado é o de atribui um valor para indicar o inicio da contagem do tempo.

4. Tendência – Método dos Mínimos Quadrados As curvas mais usuais são: 01. A Reta; 02. A Logarítmica; 03. A Exponencial.

5. Tendência – Método dos Mínimos Quadrados Exemplo 01. Considere os dados da tabela:

6. Tendência – Método dos Mínimos Quadrados Encontre a reta de Tendência que explica a quantidade de ocupações em cada dia. Solução Denotando por : x: a variável: “ Época a que se Refere os Dados, tomando dia 30 de junho como origem, e com variação dia a dia ” y: a variável: “ Número de Unidades Ocupadas” Vem:

7. Tendência – Método dos Mínimos Quadrados Perceba que com a definição de x “ Época tomando dia 30 de junho como origem,e variação dia a dia ” E com os dados originais: Primeira Semana e Segunda Feira: x =3 e y = 46; Primeira Semana e Terça Feira: x = 4 e y = 48; Primeira Semana e Quarta Feira: x =5 e y = 53; Primeira Semana e Quinta Feira: x =6 e y = 55; Segunda Semana e Segunda Feira: x =10 e y = 38 ; Etc.

8. Tendência – Método dos Mínimos Quadrados Dados Originais:

9. Tendência – Método dos Mínimos Quadrados E os valores obtidos foram: Substituindo:

10. Estimativa Pela Tendência Estimar Pela Tendência, é avaliar quanto iria ter ocorrer em cada período com o modelo matemático encontrado. Exemplo Faça a estimativa, para cada período avaliado na ocupação do Gran-Hotel. Solução Como a equação da reta ajustada foi: Vem:

11. Estimativa Pela Tendência Fazendo para cada período chega a:

12. Tendência – Método das Médias Móveis Este método consiste em: 01. Definir o número de agrupamentos, digamos k , de valores seqüenciais que comporão cada média; 02. Calcular médias dos k valores a partir do: 1 0 valor; depois a partir do 2 o , do 3 o , etc. Atribuição: Existem 2 situações possíveis sobre o valor de k ,PAR ou IMPAR , com isto considera a primeira média móvel acordo com a posição:

13. Método das Médias Móveis - Exemplo 01. Encontre as médias móveis dos dados da Tabela 1, tomando k = 7. Solução Considere as Variáveis : x: “Época, tendo dia 30 de junho como origem” y: “Numero de Unidades Ocupadas”

14. Método das Médias Móveis - Exemplo Médias Móveis com 7 períodos seqüenciais: Médias Móveis:

15. Método das Médias Móveis - Exemplo E o quadro completo de médias móveis é: Por este exemplo percebe-se que: a) A primeira média móvel refere-se ao dia 6 de julho (x = 6) b) A segunda média móvel refere-se ao dia 7 de julho (x = 7) c) A última média móvel refere-se ao dia 24 de agosto (x = 55)

16. Estimativa da Tendência Pelo Método das Médias Móveis Neste caso, basta fazer o ajuste de uma curva às médias obtidas, utilizando-se do Método dos Mínimos Quadrados. Exemplo 3 01 . Encontre a Reta de Tendência das médias móveis de 7 dias .

17. Tendência com Médias Móveis Solução Sabe-se que o ajuste é feito através das Fórmulas: Originais Cálculos

18. Tendência com Médias Móveis Fórmulas: Encontrados: Substituindo: Reta ajustada:

19. Séries Temporais Tendência Fim Prof. Gercino Monteiro Filho