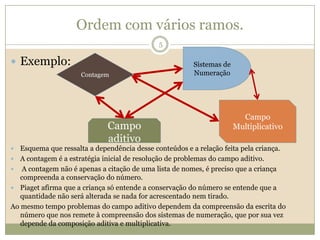
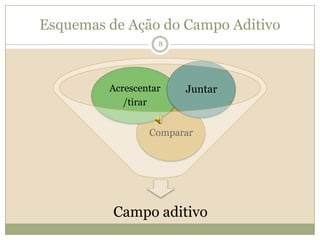
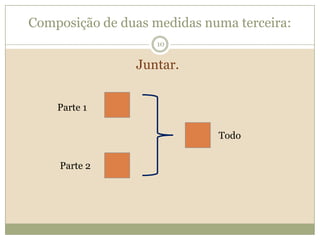
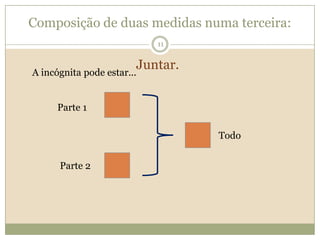
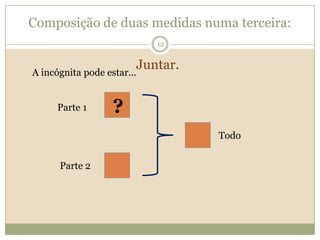
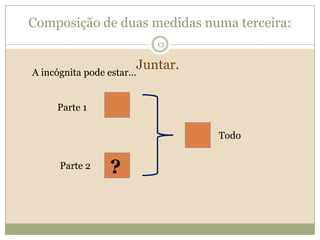
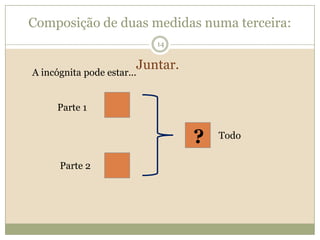
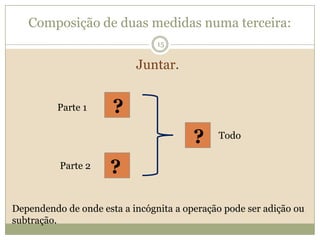
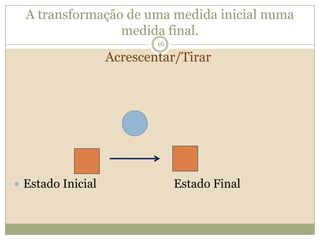
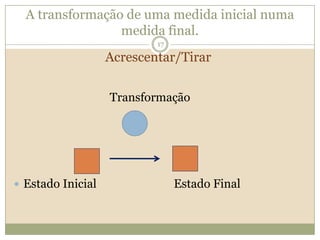
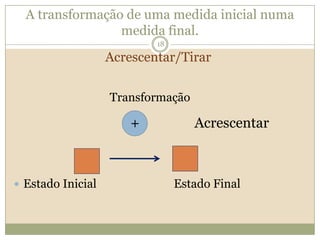
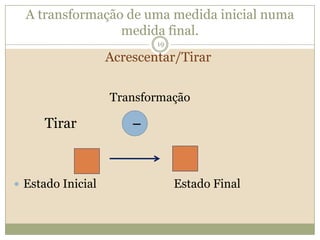
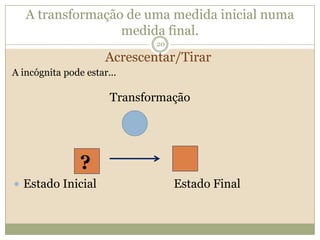
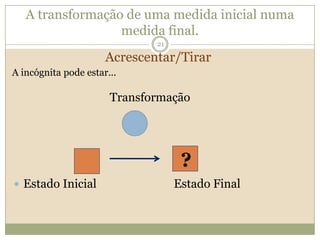
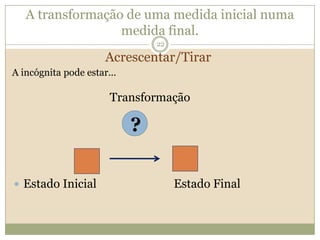
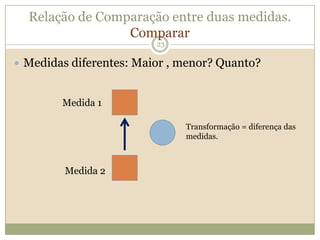
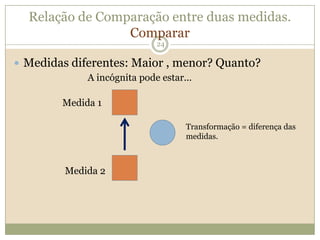
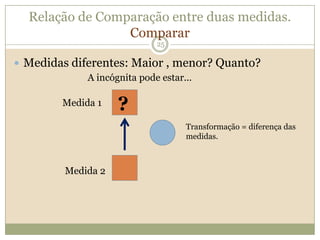
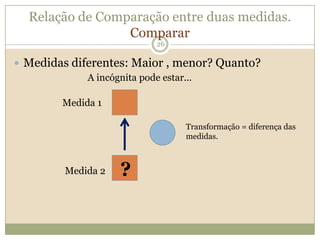
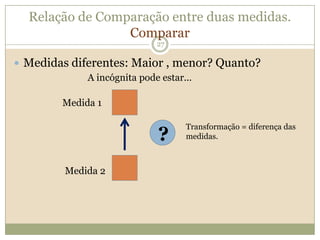
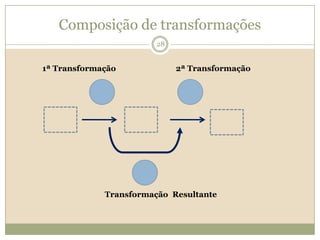
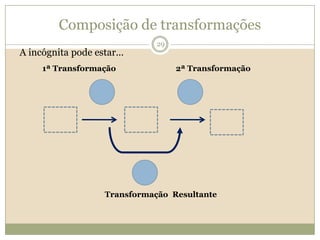
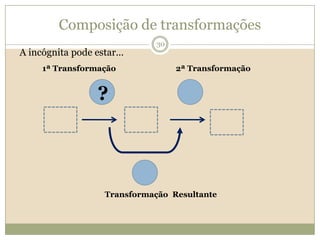
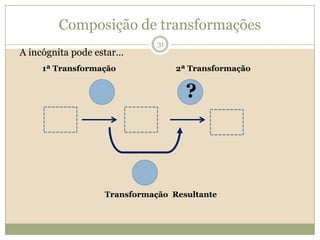
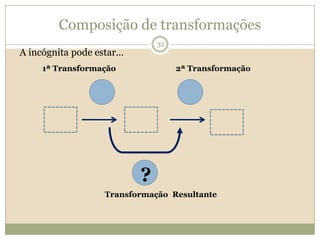
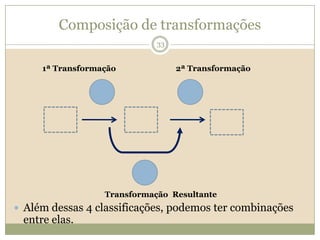
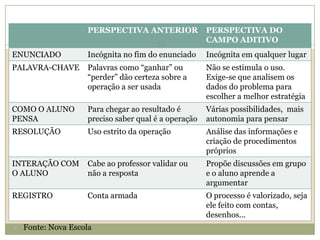
O documento discute a Teoria dos Campos Conceituais de Gérard Vergnaud, que propõe que as crianças aprendem conceitos de forma interligada e não linearmente. O Campo Aditivo é explicado, contendo esquemas como Juntar, Acrescentar e Comparar para resolver problemas matemáticos.

1. Teoria dos Campos ConceituaisSistemas de Numeração1

2. Introdução2Os problemas resolvidos no nosso 2º encontro, nos remetem aos esquemas de ação que as crianças usam para resolver problemas. Esses esquemas: Juntar, Acrescentar, Comparar, fazem parte do Campo Aditivo que por sua vez está contido na Teoria dos Campos Conceituais.

3. A Teoria dos Campos Conceituais foi idealizada por Gérard Vergnaud, psicólogo francês, discípulo de Jean Piaget e LevVygotsky, ainda atuante na área.Vergnaud investigou os processos de aprendizagem de crianças e adolescentes. A frase abaixo resume muito bem os príncipios da Teoria dos Campos Conceituais.“A ideia de Gérard Vergnaud de que se aprende na trama, não de conceitos linearmente sequenciais, mas no emaranhado de uma rede de muitos conceitos presentes em situações de vida”. (Grossi, E. , 2010).Teoria dos Campos Conceituais 3

4. Ordem linearModo usual ou como os adultos aprendem.4Também costumamos elaborar nossos planos de aula dessa forma.Vergnaud afirma que a criança aprende no emaranhado de conceitos, então se a criança apresenta dificuldade na aprendizagem, não seria esse um dos motivos?

5. Ordem com vários ramos.Exemplo:Esquema que ressalta a dependência desse conteúdos e a relação feita pela criança.A contagem é a estratégia inicial de resolução de problemas do campo aditivo. A contagem não é apenas a citação de uma lista de nomes, é preciso que a criança compreenda a conservação do número.Piaget afirma que a criança só entende a conservação do número se entende que a quantidade não será alterada se nada for acrescentado nem tirado.Ao mesmo tempo problemas do campo aditivo dependem da compreensão da escrita do número que nos remete à compreensão dos sistemas de numeração, que por sua vez depende da composição aditiva e multiplicativa. Sistemas de NumeraçãoContagemCampo MultiplicativoCampo aditivo5

6. Campo ConceitualConjunto de situações que evocam um certo conceito.É bem mais amplo que um conceito específico, pois inclui todos os problemas, tarefas cognitivas, significados e significantes que se utilizam daquele conceito.6

7. Campo aditivoConjunto de todas as situações/tarefas que exigem uma adição, uma subtração ou uma combinação dessas operações.Adição e subtração como operações irmãs.7

8. Esquemas de Ação do Campo Aditivo8

9. Classes do campo aditivo9

10. Composição de duas medidas numa terceira:Juntar.Parte 110TodoParte 2

11. Composição de duas medidas numa terceira:Juntar.A incógnita pode estar...Parte 111TodoParte 2

12. Composição de duas medidas numa terceira:Juntar.A incógnita pode estar...?12Parte 1TodoParte 2

13. Composição de duas medidas numa terceira:Juntar.A incógnita pode estar...Parte 1Todo?13Parte 2

14. Composição de duas medidas numa terceira:Juntar.A incógnita pode estar...Parte 1?14TodoParte 2

15. Composição de duas medidas numa terceira:Juntar.?Parte 1?Todo?15Parte 2Dependendo de onde esta a incógnita a operação pode ser adição ou subtração.

16. A transformação de uma medida inicial numa medida final.Estado Inicial Estado FinalAcrescentar/Tirar16

17. A transformação de uma medida inicial numa medida final. TransformaçãoEstado Inicial Estado FinalAcrescentar/Tirar17

18. A transformação de uma medida inicial numa medida final. TransformaçãoEstado Inicial Estado FinalAcrescentar/Tirar+ Acrescentar18

19. A transformação de uma medida inicial numa medida final. TransformaçãoEstado Inicial Estado FinalAcrescentar/TirarTirar 19

20. A transformação de uma medida inicial numa medida final. TransformaçãoEstado Inicial Estado FinalAcrescentar/TirarA incógnita pode estar...?20

21. A transformação de uma medida inicial numa medida final. TransformaçãoEstado Inicial Estado FinalAcrescentar/TirarA incógnita pode estar...?21

22. A transformação de uma medida inicial numa medida final. TransformaçãoEstado Inicial Estado FinalAcrescentar/TirarA incógnita pode estar...?22

23. Relação de Comparação entre duas medidas.CompararMedidas diferentes: Maior , menor? Quanto?Medida 1Transformação = diferença das medidas.23Medida 2

24. Relação de Comparação entre duas medidas.CompararMedidas diferentes: Maior , menor? Quanto?A incógnita pode estar...Medida 1Transformação = diferença das medidas.24Medida 2

25. Relação de Comparação entre duas medidas.CompararMedidas diferentes: Maior , menor? Quanto?25A incógnita pode estar...?Medida 1Transformação = diferença das medidas.Medida 2

26. Relação de Comparação entre duas medidas.CompararMedidas diferentes: Maior , menor? Quanto?26A incógnita pode estar...Medida 1Transformação = diferença das medidas.?Medida 2

27. Relação de Comparação entre duas medidas.CompararMedidas diferentes: Maior , menor? Quanto?A incógnita pode estar...Medida 1?Transformação = diferença das medidas.27Medida 2

28. Composição de transformações1ª Transformação 2ª Transformação Transformação Resultante28

29. Composição de transformaçõesA incógnita pode estar...1ª Transformação 2ª Transformação Transformação Resultante29

30. Composição de transformaçõesA incógnita pode estar...1ª Transformação 2ª Transformação ? Transformação Resultante30

31. Composição de transformaçõesA incógnita pode estar...1ª Transformação 2ª Transformação ? Transformação Resultante31

32. Composição de transformaçõesA incógnita pode estar...1ª Transformação 2ª Transformação ? Transformação Resultante32

33. Composição de transformaçõesAlém dessas 4 classificações, podemos ter combinações entre elas.1ª Transformação 2ª Transformação Transformação Resultante33

34. Fonte: Nova Escola34