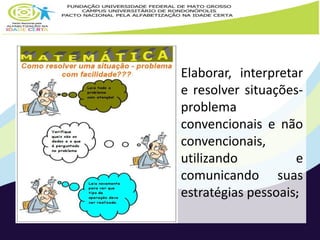
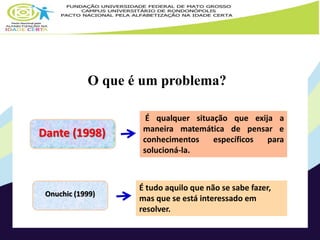
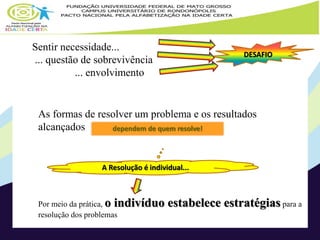
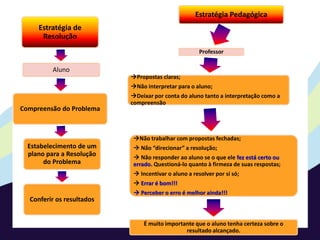
Este documento fornece subsídios teóricos e práticos para o ensino de resolução de problemas matemáticos na educação infantil. Apresenta conceitos como operações aditivas e multiplicativas, estratégias de resolução de problemas, classificação de situações-problema nos campos conceituais aditivo e multiplicativo. Também sugere atividades práticas em grupos para trabalhar diferentes tipos de situações-problema ao longo de três fases.

1. Professora Formadora na Alfabetização
Andréa Perez Leinat

2. OPERAÇÕES
NA
RESOLUÇÃO
DE
PROBLEMAS

3. Este caderno trata então, não
somente de práticas que podem
ser desenvolvidas, mas também
aborda as situações aditivas e
multiplicativas, bem como
apresenta maneiras de
desenvolver o trabalho com o
cálculo escrito (p. 5).

4. Leitura Deleite
Beleléu e as
palavras

34. Objetivos do Caderno
Oferecer subsídios teóricos e práticos
para amparar práticas pedagógicas com o
intuito de garantir que a criança possa:

35. Elaborar, interpretar e
resolver situações-problema
do campo aditivo (adição e
subtração) e multiplicativo
(multiplicação e divisão),
utilizando e comunicando
suas estratégias pessoais,
envolvendo os seus
diferentes significados;

36. Calcular adição e subtração com e sem
agrupamento e desagrupamento;

37. Construir estratégias de cálculo mental e
estimativo, envolvendo dois ou mais termos;

38. Elaborar, interpretar
e resolver situações-problema
convencionais e não
convencionais,
utilizando e
comunicando suas
estratégias pessoais;

40. ?????  O que é um problema?
 Por que resolver um
problema?
 Como resolver um
problema?

41. O que é um problema?
Dante (1998)
Onuchic (1999)
É qualquer situação que exija a
maneira matemática de pensar e
conhecimentos específicos para
solucioná-la.
É tudo aquilo que não se sabe fazer,
mas que se está interessado em
resolver.

42. Sentir necessidade...
... questão de sobrevivência
... envolvimento
DESAFIO
As formas de resolver um problema e os resultados
alcançados dependem de quem resolve!
A Resolução é individual...
Por meio da prática, o indivíduo estabelece estratégias para a
resolução dos problemas

43. Estratégias
envolvidas na
Resolução de
problemas...

44. Estratégia de
Resolução
Aluno
Compreensão do Problema
Estabelecimento de um
plano para a Resolução
do Problema
Conferir os resultados
Estratégia Pedagógica
Professor
Propostas claras;
Não interpretar para o aluno;
Deixar por conta do aluno tanto a interpretação como a
compreensão
Não trabalhar com propostas fechadas;
 Não “direcionar” a resolução;
 Não responder ao aluno se o que ele fez está certo ou
errado. Questioná-lo quanto à firmeza de suas respostas;
 Incentivar o aluno a resolver por sí só;
 Errar é bom!!!
 Perceber o erro é melhor ainda!!!
É muito importante que o aluno tenha certeza sobre o
resultado alcançado.

45. POR EXEMPLO...

48. POR ISSO...

49. Para melhor conceituarmos o que é uma
situação-problema, podemos dizer que é
toda e qualquer situação onde se deseja
obter uma solução, cuja resposta exige pôr
à prova tudo o que se sabe. Contudo, a
resolução de um problema pode ser
complexa para um determinado aluno e
simples para outro.

51. A TEORIA DOS CAMPOS
CONCEITUAIS ADITIVAS E
MULTIPLICATIVAS

52. Professor, que conta
tem que fazer? É de
mais ou de menos? É
de vezes ou de dividir?

53. Vergnaud (2009) afirma que conceitos não
podem ser compreendidos de modo isolado,
mas sim a partir de campos conceituais.

54. Isto implica em considerar que conceitos, como
por exemplo, de adição e subtração, envolvem e
são envolvidos por situações, estruturas,
operações de pensamento e representação que
se relacionam entre si.
Assim, adição e subtração fazem
parte de um mesmo campo
conceitual denominado aditivo.

55. Do mesmo modo,
multiplicação e divisão
fazem parte do campo
conceitual denominado
multiplicativo (p. 17/18).

56. CLASSIFICAÇÃO DO CAMPO
CONCEITO ADITIVO..

57. Página 19, 20 e 21
1º - COMPOSIÇÃO SIMPLES
Em um vaso há 5 rosas amarelas e 3 rosas vermelhas.
Quantas rosas há ao todo no vaso?
2º - TRANSFORMAÇÃO SIMPLES
Aninha tem 3 pacotes de figurinhas. Ganhou 4 pacotes da
sua avó. Quantos pacotes tem agora?
Zeca tinha 7 bolinhas de gude. Deu 3 para Luís. Quantas
ele tem agora?

58. 3º - COMPOSIÇÃO COM UMA DAS PARTES
DESCONHECIDA
Em um vaso há 8 rosas, 3 são vermelhas e as outras são
amarelas. Quantas rosas amarelas há no vaso?
4º - TRANSFORMAÇÃO COM TRANSFORMAÇÃO
DESCONHECIDA
Aninha tinha 5 bombons. Ganhou mais alguns bombons de
Júlia. Agora Aninha tem 8 bombons. Quantos bombons
Aninha ganhou?
Zeca tinha 8 bombons. Deu alguns bombons para Luís e
ficou com 3. Quantos bombons Zeca deu para Luís?
Páginas 23, 24 e 25

59. 5º - TRANSFORMAÇÃO COM INÍCIO
DESCONHECIDO
Maria tinha algumas figurinhas. Ganhou 4 figurinhas de Isa.
Agora Maria tem 7 figurinhas. Quantas figurinhas Maria tinha?
Paulo tinha alguns carrinhos. Deu 4 carrinhos para Pedro e
ficou com 7. Quantos carrinhos Paulo tinha?
Páginas 26 e 27
6º - COMPARAÇÃO
João tem 7 carrinhos e José tem 4 carrinhos. Quem tem mais
carrinhos?
João tem 7 carrinhos e José tem 4 carrinhos. Quantos
carrinhos João tem a mais do que José?

60. CLASSIFICAÇÃO DO
CAMPO CONCEITUAL...

61. Página 19, 20 e 21
1º - COMPARAÇÕA ENTRE RAZÕES
Em uma caixa de lápis de cor há 12 lápis. Quantos lápis há
em 3 caixas iguais a esta?
2º - DIVISÃO POR DISTRIBUIÇÃO
Júlia ganhou 12 chocolates e quer dividir entre 4 amigos
de sua sala de aula. Quantos chocolates cada um vai
receber?

62. 3º - DIVISÃO ENVOLVENDO FORMAÇÃO DE
GRUPOS
Dona Centopeia levou 20 caixas de sapatos em sacolas.
Em cada sacola foram colocadas 4 caixas de sapatos.
Quantas sacolas foram utilizadas?
4º - CONFIGURAÇÃO RETANGULAR
Dona Centopeia organizou seus sapatos em 7 fileiras com
5 caixas empilhadas. Quantas caixas de sapatos dona
Centopeia organizou?
Páginas 23, 24 e 25

63. 5º - RACIOCÍNIO COMBINATÓRIO
Dona Centopeia tem dois chapéus, um
branco (B) e outro preto (P) e três bolsas,
uma rosa (R), uma azul (A) e uma cinza
(C). De quantas maneiras diferentes Dona
Centopeia pode escolher seus acessórios
para ir passear?
Páginas 26 e 27

64. Ler os encartes especial Matemática :
Operações irmãs;
De vezes e de dividir.

65. VAMOS TRABALHAR...

66. Trabalho por fases e por escola :
analisar possibilidades de trabalho a
partir dos eixos, dos direitos, das
capacidades e socializa-las:
• Grupo 1: Situação Aditiva e Situação Simples(p.
18 a 20); 1ª fase
• Grupo 2: Situação de Transformação Simples e
Situação de Composição com uma das partes
desconhecida (p. 21 a 24); 1ª fase

67. • Grupo 3: Situação de Transformação com
Transformação desconhecida e Situações de
Transformação com Estado Inicial
Desconhecido (p. 24 a 26); 1ª fase
• Grupo 4: Situação de Comparação (p. 27 a 29);
1ª fase
• Grupo 5: Corrida dos Carrinhos (p. 30/31); 1ª
fase

68. • Grupo 3: Situação de Transformação com
Transformação desconhecida e Situações de
Transformação com Estado Inicial Desconhecido
(p. 24 a 26); 1ª fase
• Grupo 4: Situação de Comparação (p. 27 a 29);
1ª fase
• Grupo 5: Corrida dos Carrinhos (p. 30/31); 1ª fase

69. • Grupo 6: Situação de Multiplicativas e Situações
de Comparação entre Razões (p. 31 a 35); 2ª fase
• Grupo 7: Situação de Divisão por Distribuição (p.
35 a 37); 2ª fase
• Grupo 8: Situação de Divisão envolvendo
formação de grupos e Situação de Configuração
Retangular (p. 37 a 40 ); 2ª fase

70. • Grupo 9: Situação Envolvendo Raciocínio
Combinatório (p. 40 a 42); 2ª fase
• Grupo 10: Sobre Cálculos e Algoritmos
Contagem (p. 43 a 47); 2ª fase
• Grupo 11: Uso da Tabuada em Sla de Aula(p.
49a 54 ); 3ª fase

71. • Grupo 12: Dobro e Metades (p. 54 a 58); 3ª
fase
• Grupo 13: Sobre Cálculos e Algoritmos
Contagem (p. 43 a 47); 3ª fase
• Grupo 11: Uso da Tabuada em Sala de Aula (p.
49a 54 ); 3ª fase

72. • Grupo 14: Adição sem agupamento ou reserva
(p. 61/ 62) e Adição com agrupamento ou
reserva (p. 64 a 67) 3ª fase
• Grupo 15: Subtração sem desagupamento ou
(p. 62 a 64) e Subtração com
desagrupamento (p. 67 a 69) 3ª fase

73. PARA CONCLUIR...

74. Este caderno apresentou vários conceitos
referentes à Resolução de Problemas e às
operações. Certamente, são muitas informações
para dominarmos. No entanto, na rotina de sala
de aula, ao abrirmos um livro didático, atual e
aprovado pelo PNLD, por exemplo,
observaremos que todos estes conceitos estão
ali presentes. Ter consciência deste fato é muito
importante para alterar a prática tradicional,
evitando a repetição de resoluções de um
grande número de problemas sempre do
mesmo tipo.