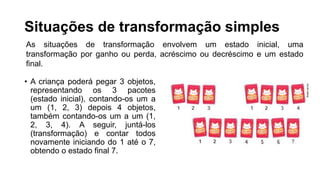
O documento descreve diferentes tipos de situações aditivas e subtrativas que as crianças encontram no processo de alfabetização matemática, incluindo situações de composição, transformação e comparação. Essas situações envolvem adição e subtração e ajudam as crianças a desenvolver estratégias de contagem. Problemas mais complexos podem envolver partes desconhecidas ou estados iniciais/finais desconhecidos.

1. ADIÇÃO E SUBTRAÇÃO
Sob a perspectiva da Teoria dos Campos Conceituais, adicionar e
subtrair são ações vinculadas ao campo aditivo.
Bruna Ricci
Isabela Nery Azevedo
Thaís de Carvalho Garcia

2. • A vivência trazida pela criança no início do processo de escolarização não é
pequena e, acrescentamos, não deve ser ignorada. Ao ingressarem na escola,
as crianças já conseguem resolver problemas que envolvem situações aditivas
simples, coordenando ações de “juntar”, “ganhar” e “perder”
• A atividade de contagem permite que as crianças construam estratégias que lhes
possibilitam resolver problemas de complexidade crescente, e, para isso, requer
o desenvolvimento de algumas habilidades: começar a contagem a partir de
qualquer ponto arbitrário da série numérica; identificar o último objeto contado
como o cardinal que expressa a quantidade total sem necessidade de contar os
objetos novamente; estender a contagem iniciada no primeiro conjunto ao
segundo conjunto de tal forma que o primeiro objeto deste seja considerado o
número seguinte na sequência de contagem
• Com o tempo, e à medida que interagem com diferentes situações, desenvolvem
estratégias de contagem mais sofisticadas, abstratas e eficientes, tais como as
necessárias para a resolução de problemas aditivos

3. Situações de composição simples
• As situações de composição relacionam as partes que
compõem um todo por ações de juntar ou separar as partes
para obter o todo sem promover transformação em nenhuma
das partes.
• A criança poderá pegar 5 objetos azuis, contando-os um a um
(1, 2, 3, 4, 5) depois 3 objetos vermelhos, também contando-os
um a um (1, 2, 3). A seguir, juntar ambos os grupos para saber
o total e contar todos novamente iniciando do 1 até o 8. Esse
procedimento é descrito na literatura como “contar todos”.

4. Situações de transformação simples
• A criança poderá pegar 3 objetos,
representando os 3 pacotes
(estado inicial), contando-os um a
um (1, 2, 3) depois 4 objetos,
também contando-os um a um (1,
2, 3, 4). A seguir, juntá-los
(transformação) e contar todos
novamente iniciando do 1 até o 7,
obtendo o estado final 7.
As situações de transformação envolvem um estado inicial, uma
transformação por ganho ou perda, acréscimo ou decréscimo e um estado
final.

5. Situações de transformação simples
• Também poderia pegar 3
pacotes de figurinhas e
continuar pegando mais 4
pacotes, um a um, continuando
a contagem até 7. Esse
procedimento é conhecido
como “contar na sequência”.
Problemas de subtração também podem envolver situações de
transformação simples e podem ser resolvidos a partir da
coordenação das ações de retirar e contar.

6. Situação de composição com uma das
partes desconhecida
Em um vaso há 8 rosas, 3 são
vermelhas e as outras são
amarelas. Quantas rosas amarelas
há no vaso?
- Todo: 8 rosas
- Parte conhecida: 3 rosas
vermelhas
- Parte desconhecida: ?
Situações problemas em que o todo e uma das partes são conhecidos,
sendo necessário determinar a outra parte. Por exemplo:

7. Situações de transformação com
transformação desconhecida
Zeca tinha 8 bombons. Deu alguns
bombons para Luís e ficou com 3.
Quantos bombons Zeca deu para
Luís?
– Estado inicial: 8 bombons
– Transformação: ?
– Estado final: 3 bombons
São problemas aditivos de transformação desconhecida, uma vez que são
conhecidos os estados iniciais e o estado final da situação. Por exemplo:

8. Situações de transformação com
estado inicial desconhecido
O estado inicial também pode ser desconhecido nas situações
de transformação. Esses problemas costumam ser mais difíceis
para as crianças, pois envolvem operações de pensamento mais
complexas. Por exemplo:
Maria tinha algumas figurinhas. Ganhou 4 figurinhas de Isa.
Agora Maria tem 7 figurinhas. Quantas figurinhas Maria tinha?
- Estado inicial: ?
- Transformação: ganhou 4 figurinhas
- Estado final: 7 figurinhas

9. Situações de comparação
Nessa situação não há
transformação, uma vez que nada é
tirado ou acrescentado ao todo ou
às partes, mas uma relação de
comparação entre as quantidades
envolvidas. Por exemplo:
- João tem 7 carrinhos e José tem 4
carrinhos. Quem tem mais
carrinhos?
- João tem 7 carrinhos e José tem 4
carrinhos. Quantos carrinhos João
tem a mais do que José ?
“Nunes et. al. (2005), sugerem que uma
boa estratégia para ajudar as crianças a
pensarem sobre “quantos tem a mais” é
solicitar que relacionem os números
envolvidos no problema a partir de uma
ação, reformulando a pergunta do
problema. Por exemplo: quantos
carrinhos temos que dar a José para
que ele fique com a mesma quantidade
de João? Pensando dessa forma o
problema se torna semelhante a um
problema de transformação
desconhecida: 4 + ? = 7, tornando-se
mais fácil de ser resolvido por envolver
uma informação mais precisa em
relação à ação a ser realizada.”

10. Problematizando situações após o
jogo

12. Referência
BRASIL. Secretaria de Educação Básica. Diretoria de Apoio à
Gestão Educacional. Pacto Nacional pela Alfabetização na
Idade Certa: Operações na resolução de problemas / Ministério
da Educação, Secretaria de Educação Básica, Diretoria de
Apoio à Gestão Educacional. – Brasília: MEC, SEB, 2014.