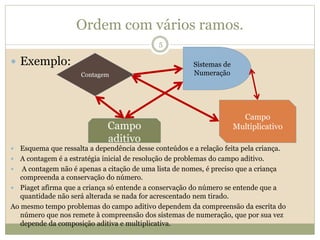
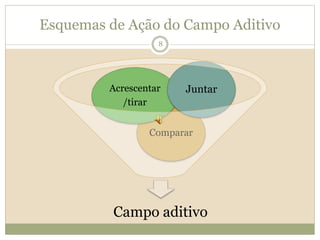
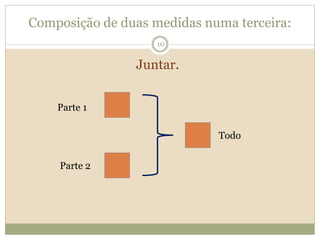
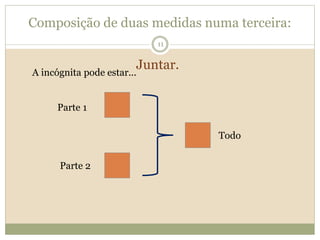
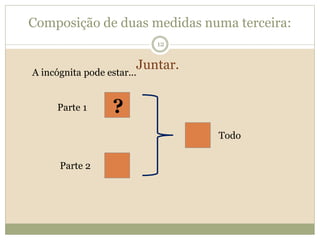
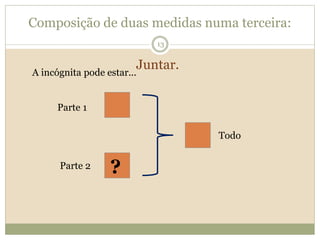
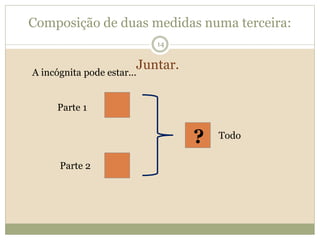
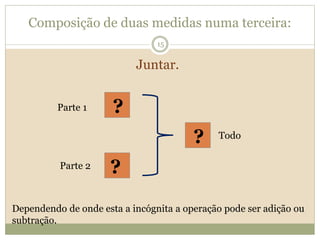
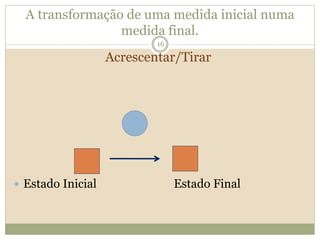
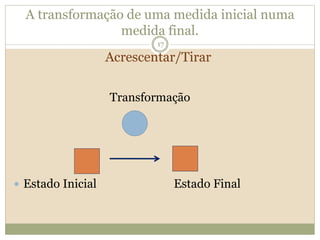
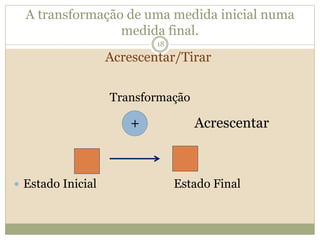
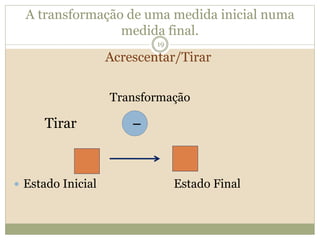
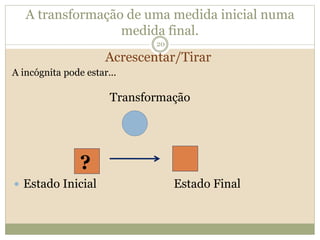
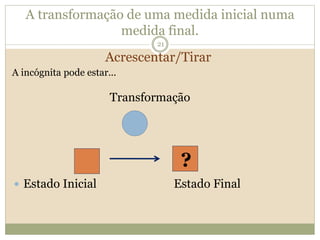
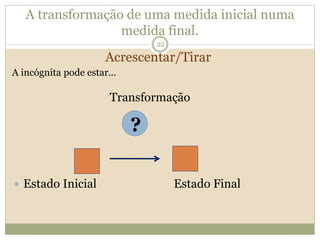
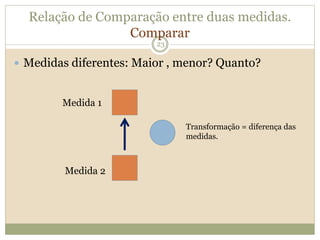
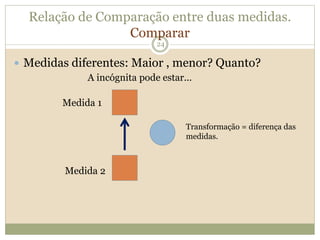
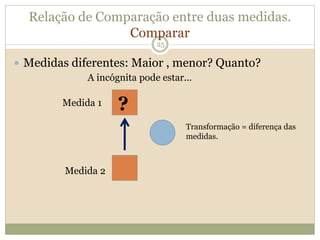
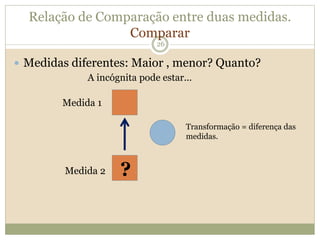
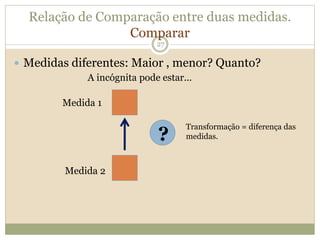
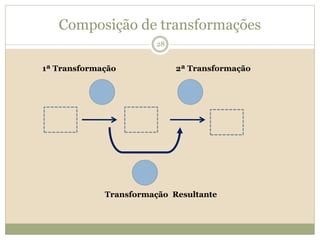
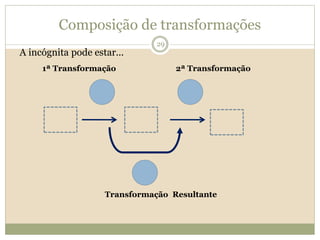
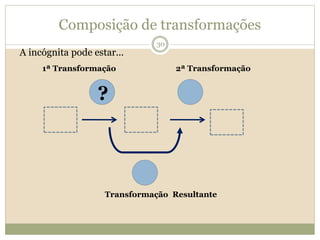
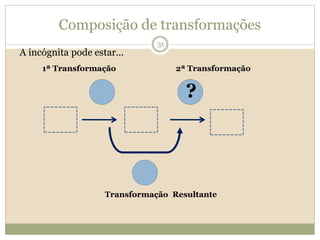
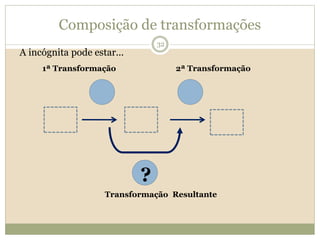
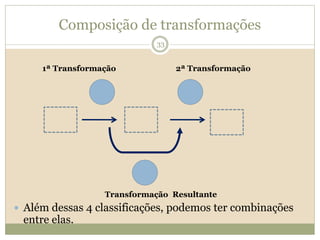
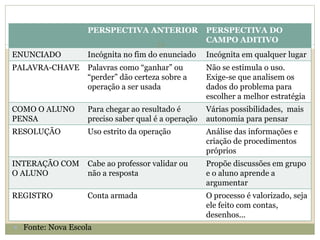
O documento descreve a Teoria dos Campos Conceituais de Gérard Vergnaud, que estuda como as crianças aprendem conceitos de forma interligada em vez de linear. O Campo Aditivo é apresentado como um exemplo, envolvendo esquemas como Juntar, Acrescentar e Comparar. Problemas do Campo Aditivo dependem de conceitos como Sistemas de Numeração e Campo Multiplicativo.

1. T E O R I A D O S C A M P O S C O N C E I T U A I S
Sistemas de Numeração
1

2. Introdução
2
 Os problemas resolvidos no nosso 2º encontro, nos
remetem aos esquemas de ação que as crianças usam
para resolver problemas.
 Esses esquemas: Juntar, Acrescentar, Comparar,
fazem parte do Campo Aditivo que por sua vez está
contido na Teoria dos Campos Conceituais.

3.  A Teoria dos Campos Conceituais foi
idealizada por Gérard Vergnaud,
psicólogo francês, discípulo de Jean
Piaget e Lev Vygotsky, ainda atuante na
área.
 Vergnaud investigou os processos de
aprendizagem de crianças e
adolescentes.
 A frase abaixo resume muito bem os
príncipios da Teoria dos Campos
Conceituais.
“A ideia de Gérard Vergnaud de que se
aprende na trama, não de conceitos
linearmente sequenciais, mas no
emaranhado de uma rede de muitos
conceitos presentes em situações de
vida”. (Grossi, E. , 2010).
Teoria dos Campos Conceituais
3

4. Ordem linear
Modo usual ou como os adultos aprendem.
4
Também costumamos elaborar nossos planos de
aula dessa forma.
Vergnaud afirma que a criança aprende no
emaranhado de conceitos, então se a criança
apresenta dificuldade na aprendizagem, não seria esse
um dos motivos?

5. Ordem com vários ramos.
 Exemplo:
 Esquema que ressalta a dependência desse conteúdos e a relação feita pela criança.
 A contagem é a estratégia inicial de resolução de problemas do campo aditivo.
 A contagem não é apenas a citação de uma lista de nomes, é preciso que a criança
compreenda a conservação do número.
 Piaget afirma que a criança só entende a conservação do número se entende que a
quantidade não será alterada se nada for acrescentado nem tirado.
Ao mesmo tempo problemas do campo aditivo dependem da compreensão da escrita do
número que nos remete à compreensão dos sistemas de numeração, que por sua vez
depende da composição aditiva e multiplicativa.
Sistemas de
Numeração
Campo
MultiplicativoCampo
aditivo
Contagem
5

6. Campo Conceitual
 Conjunto de situações que evocam um certo
conceito.
 É bem mais amplo que um conceito específico, pois
inclui todos os problemas, tarefas cognitivas,
significados e significantes que se utilizam daquele
conceito.
6

7. Campo aditivo
 Conjunto de todas as situações/tarefas que exigem
uma adição, uma subtração ou uma combinação
dessas operações.
 Adição e subtração como operações irmãs.
7

8. Esquemas de Ação do Campo Aditivo
Campo aditivo
Comparar
Acrescentar
/tirar
Juntar
8

9. Classes do campo aditivo
9

10. Composição de duas medidas numa terceira:
Juntar.
10
Parte 2
Parte 1
Todo

11. Composição de duas medidas numa terceira:
Juntar.
11
Parte 2
Parte 1
Todo
A incógnita pode estar...

12. Composição de duas medidas numa terceira:
?
Juntar.
12
Parte 2
Parte 1
Todo
A incógnita pode estar...

13. Composição de duas medidas numa terceira:
?
Juntar.
13
Parte 2
Parte 1
Todo
A incógnita pode estar...

14. Composição de duas medidas numa terceira:
?
Juntar.
14
Parte 2
Parte 1
Todo
A incógnita pode estar...

15. Composição de duas medidas numa terceira:
?
?
?
Juntar.
15
Parte 2
Parte 1
Todo
Dependendo de onde esta a incógnita a operação pode ser adição ou
subtração.

16. A transformação de uma medida inicial numa
medida final.
 Estado Inicial Estado Final
Acrescentar/Tirar
16

17. A transformação de uma medida inicial numa
medida final.
Transformação
 Estado Inicial Estado Final
Acrescentar/Tirar
17

18. A transformação de uma medida inicial numa
medida final.
Transformação
 Estado Inicial Estado Final
+ Acrescentar
Acrescentar/Tirar
18

19. A transformação de uma medida inicial numa
medida final.
Transformação
 Estado Inicial Estado Final
Tirar 
Acrescentar/Tirar
19

20. A transformação de uma medida inicial numa
medida final.
Transformação
 Estado Inicial Estado Final
?
Acrescentar/Tirar
20
A incógnita pode estar...

21. A transformação de uma medida inicial numa
medida final.
Transformação
 Estado Inicial Estado Final
?
Acrescentar/Tirar
21
A incógnita pode estar...

22. A transformação de uma medida inicial numa
medida final.
Transformação
 Estado Inicial Estado Final
?
Acrescentar/Tirar
22
A incógnita pode estar...

23. Relação de Comparação entre duas medidas.
Comparar
 Medidas diferentes: Maior , menor? Quanto?
23
Medida 1
Medida 2
Transformação = diferença das
medidas.

24. Relação de Comparação entre duas medidas.
Comparar
 Medidas diferentes: Maior , menor? Quanto?
24
Medida 1
Medida 2
Transformação = diferença das
medidas.
A incógnita pode estar...

25. Relação de Comparação entre duas medidas.
Comparar
 Medidas diferentes: Maior , menor? Quanto?
25
Medida 1
Medida 2
Transformação = diferença das
medidas.
?
A incógnita pode estar...

26. Relação de Comparação entre duas medidas.
Comparar
 Medidas diferentes: Maior , menor? Quanto?
26
Medida 1
Medida 2
Transformação = diferença das
medidas.
?
A incógnita pode estar...

27. Relação de Comparação entre duas medidas.
Comparar
 Medidas diferentes: Maior , menor? Quanto?
?
27
Medida 1
Medida 2
Transformação = diferença das
medidas.
A incógnita pode estar...

28. Composição de transformações
1ª Transformação 2ª Transformação
Transformação Resultante
28

29. Composição de transformações
1ª Transformação 2ª Transformação
Transformação Resultante
29
A incógnita pode estar...

30. Composição de transformações
?
1ª Transformação 2ª Transformação
Transformação Resultante
30
A incógnita pode estar...

31. Composição de transformações
?
1ª Transformação 2ª Transformação
Transformação Resultante
31
A incógnita pode estar...

32. Composição de transformações
?
1ª Transformação 2ª Transformação
Transformação Resultante
32
A incógnita pode estar...

33. Composição de transformações
 Além dessas 4 classificações, podemos ter combinações
entre elas.
1ª Transformação 2ª Transformação
Transformação Resultante
33

34.  Fonte: Nova Escola
PERSPECTIVA ANTERIOR PERSPECTIVA DO
CAMPO ADITIVO
ENUNCIADO Incógnita no fim do enunciado Incógnita em qualquer lugar
PALAVRA-CHAVE Palavras como “ganhar” ou
“perder” dão certeza sobre a
operação a ser usada
Não se estimula o uso.
Exige-se que analisem os
dados do problema para
escolher a melhor estratégia
COMO O ALUNO
PENSA
Para chegar ao resultado é
preciso saber qual é a operação
Várias possibilidades, mais
autonomia para pensar
RESOLUÇÃO Uso estrito da operação Análise das informações e
criação de procedimentos
próprios
INTERAÇÃO COM
O ALUNO
Cabe ao professor validar ou
não a resposta
Propõe discussões em grupo
e o aluno aprende a
argumentar
REGISTRO Conta armada O processo é valorizado, seja
ele feito com contas,
desenhos...
34