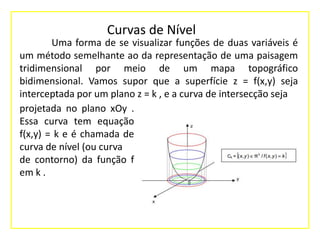
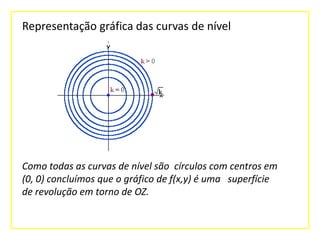
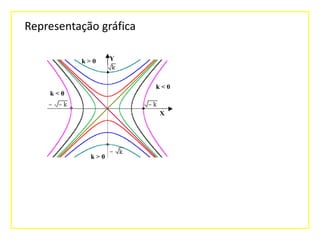
O documento explica o que são curvas de nível e como elas representam gráficamente funções de duas variáveis. As curvas de nível são conjuntos de pontos no plano xOy com a mesma imagem z. O documento fornece exemplos de curvas de nível para funções como z=x2+y2 e discute como elas podem representar quantidades físicas como temperatura, pressão e potencial.

1. Curvas
de
nível
Professor : Walmir E. Pottiter
Aluno: Fernando T. Niekawa
Curso: Licenciatura em química
Disciplina: Cálculo II

2. Curvas de Nível
Uma forma de se visualizar funções de duas variáveis é
um método semelhante ao da representação de uma paisagem
tridimensional por meio de um mapa topográfico
bidimensional. Vamos supor que a superfície z = f(x,y) seja
interceptada por um plano z = k , e a curva de intersecção seja
projetada no plano xOy .
Essa curva tem equação
f(x,y) = k e é chamada de
curva de nível (ou curva
de contorno) da função f
em k .

3. As curvas de nível de uma função f de duas
variáveis são gráficos no plano xOy de equações da
forma f(x,y) = k .
O conjunto de curvas de nível é chamado
mapa de contorno.
Todos os pontos (x,y) que estão na mesma
curva de nível têm a mesma imagem z.
No caso de f(x,y) representar uma grandeza
física, as curvas de nível ganham particular
importância, recebendo inclusive denominações
específicas.

4. Se f(x,y) é a temperatura no ponto (x,y) de uma
chapa plana, as curvas f(x,y) = k
são chamadas de isotérmicas ou isotermas.
 Se f(x,y) é a pressão de um gás de volume x e
temperatura y , as curvas são chamadas
de isobáricas ou isóbaras.
 Se f(x,y) é o potencial (elétrico ou gravitacional) na
região D do plano xOy então as curvas
f(x,y) = k são chamadas equipotenciais.

5. Exemplo
Seja a função dada por z = x2 + y2
As curvas de nível para z = 0, z =1, z = 2 e z = 4 são:
z = 0 ⇒ x2 + y2 = 0 (x = y = 0 )
z = 1 ⇒ x2 + y2 = 1 (circunferência de centro C(0,0) e raio 1)
z = 2 ⇒ x2 + y2 = 2 (circunferência de centro C(0,0) e raio 2 )
z = 4 ⇒ x2 + y2 = 4 (circunferência de centro C(0,0) e raio 2)
Observação: As curvas de nível nunca se interceptam

6. Gráfico da Função (Parabolóide Elíptico)
Observação: As funções de três ou mais variáveis
não podem ser representadas graficamente.

7. Exercícios resolvidos:
I) f(x, y) = x2 + y2
Curvas de nível
Seja a equação x2 + y2 = k.
Como x2 ³ 0 e y2 ³ 0 então se k < 0 a equação não tem
solução. Ou seja, para qualquer k < 0 (abaixo do plano
XOY) a curva de nível correspondente é o f .

8. Fazendo k = 0 (intersecção com o plano XOY),
a equação x2 + y2 = 0 tem solução x = 0 e y = 0.
A curva de nível em z = 0 é (0, 0).
Fazendo k > 0, a equação x2 + y2 = k pode ser escrita como
x2
y2
( k )2
k
Portanto para qualquer k > 0 a curva de nível correspondente
é um círculo de raio
k
e centro na origem do ( R² ).

9. Representação gráfica das curvas de nível
Como todas as curvas de nível são círculos com centros em
(0, 0) concluímos que o gráfico de f(x,y) é uma superfície
de revolução em torno de OZ.

10. Exercício
II) f (x, y) = y2 - x2
Curvas de nível
Seja a equação y2 - x2 = k.
Se k = 0, temos x2 = y2 Û x = y ou x = -y, ou seja, as retas
1a e 2a bissetrizes.
Se k > 0, podemos escrever a equação y2 - x2 = k como
y2
( k)
x2
2
( k)
2
1

11. Neste caso temos uma hipérbole com focos sobre o eixo OY
Se k < 0 então – k > 0 , podemos escrever a equação (*) como
x
(
2
k)
y
2
(
2
k)
2
1
Neste caso temos também uma hipérbole com focos sobre o
eixo OX.

12. Representação gráfica

13. Referências:
http://www.pucrs.br/famat/demat/facin/calcb/material_200502/Topico_08_Funcoes
_de_duas_ou_mais_variaveis.pdf
http://www.mat.ufba.br/mat042/aula24/aula24.htm#ind