1. O documento apresenta definições e propriedades de potenciação e radiciação, incluindo casos particulares, condições de existência e propriedades.
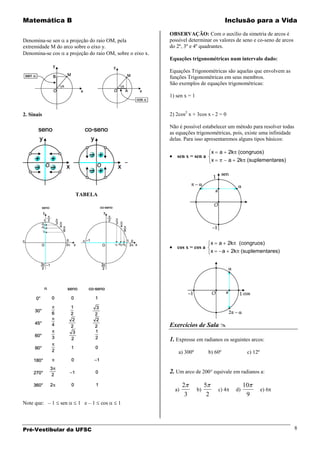
2. A segunda unidade trata de trigonometria no triângulo retângulo, apresentando relações trigonométricas e exemplos de aplicação no triângulo equilátero e no quadrado.
3. A terceira unidade aborda o Teorema dos Cossenos para triângulos quaisquer.










![Matemática B Inclusão para a Vida
Tarefa Mínima 32. Se sen x 0, então cosec x 0.
64. A solução da equação 2sen2x + 3sen x = 2 para
1. Determine o valor de: 5
0 x 2 é x= ou x = .
6 6
a) sec 60o b) cossec 150o c) cotg 315o
2. (Faap-SP)Se sen x = 3/5, com x 4º quadrante, 3
9. (UFSC) Dado sen x = ex 0 , calcule o
então tg x é: 5 2
valor numérico da expressão:
a) 3/4 b) 1/2 2 1
c) 4/5 d) 3/4 sec x cotgx cosecx tgx
e) 4/5 6 senx cosec2 x
3
3. ( UFSC ) Dados sen x = e x , determine
5 2 10. (FATEC) Se x e y são números reais tais que
o valor de: 32 tg x + 1 e x e xtg 4 x
y= , então:
4. ( FGV-SP ) Simplificando-se a expressão
sec x tg 2 x.sec x
sena tga coseca
, obtém-se: a) y = ex b) y = ex(1 + tg x)
cosa cotga seca
ex ex
c) y = d) y =
a) 0 b) sec2a cos x sec x
c) sen2a d) 1 e) n.d.a.
e) tg2a
Tarefa Complementar UNIDADES 8 e 9
5. (UFSC)Sabendo que cossec x = 5/4 e x é do primeiro
quadrante, então o valor da expressão 9.(sec2 x + tg2 x) é: GEOMETRIA ANALÍTICA
ESTUDO DO PONTO
6. (UFSC) Calcule o valor numérico da expressão: O sistema cartesiano ortogonal, como já vimos em
sen30 cos120 cosec150 cotg330 funções, é composto por duas retas x e y perpendiculares
sec300 tg60 cotg225 entre si, no ponto O (origem). A reta x é denominada eixo
das abscissas, e a reta y é denominada eixo das ordenadas.
Os dois eixos dividem o plano em quatro regiões
7. (UFCE) Para todo x 1º quadrante, a expressão denominadas quadrantes numerados no sentido anti-
(sec x - tg x)(sec x + tg x) sen2x é igual a: horário.
a) cos2x b) 1 + sen2x
c) cos x - sen x d) sec x + cos x
e) n.d.a.
8. Determine a soma dos números associados à(s)
proposição(ões) correta(s).
01. A medida em radianos de um arco de 225º é
11π
rad.
6
02. A menor determinação positiva de um arco de A cada ponto do plano cartesiano está associado um par
1000° é 280°. ordenado (x, y).
04. Os valores de m, de modo que a expressão
sen x = 2m – 5 exista, estão no intervalo [2,3].
08. sen x > cos x para x .
4 4
3 3
16. Se tg x = e x , então o valor de
4 2
1
sen x – cos x é igual a .
5
Pré-Vestibular da UFSC 12](https://image.slidesharecdn.com/matpotenciacaoeradiciacao-111215170019-phpapp01/85/Mat-potenciacao-e-radiciacao-12-320.jpg)








