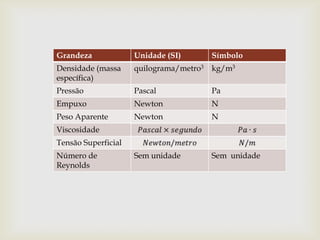
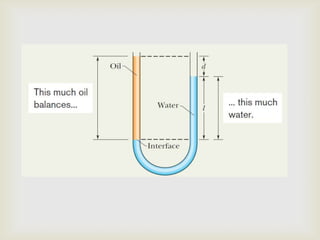
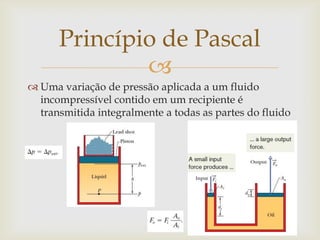
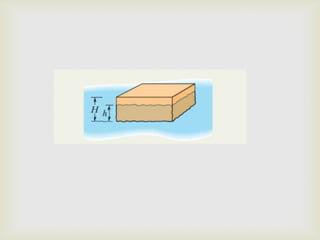
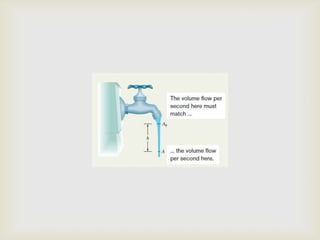
O documento introduz conceitos básicos sobre transporte de fluidos, incluindo massa específica, pressão, empuxo, peso aparente, viscosidade e número de Reynolds. Exemplos ilustram os princípios de Pascal, Arquimedes e Bernoulli, além de equações como a da continuidade e leis de Poiseuille e Stokes.

1. Introdução ao Fenômeno de Transporte de
Fluidos

2. Grandeza Unidade (SI) Símbolo
Densidade (massa
específica)
quilograma/metro3 kg/m3
Pressão Pascal Pa
Empuxo Newton N
Peso Aparente Newton N
Viscosidade
Tensão Superficial
Número de
Reynolds
Sem unidade Sem unidade

3. 
 Massa Específica (Densidade)
 Densidade Uniforme
1.1 Propriedades Básicas
dos Fluidos

4. Pressão
Pressão uniforme

5. 
 Uma sala de estar tem 4,2 m de comprimento, 3,5 m
de largura e 2,4 m de altura.
 (a) Qual é o peso do ar contido na sala se a pressão
do ar é 1 atm?
 (b) Qual é o módulo da força que a atmosférica
exerce, de cima para baixo, sobre a cabeça de uma
pessoa, que tem uma área de 0,04 m2?
Exemplo
Pressão atmosférica e força

6. 
 (a) Usando a densidade do ar para 1 atm
 (b) A pressão na área é uniforme
Resposta

7. 
 A água dentro do cilindro se encontra em equilíbrio estático.
 A pressão em um ponto do fluido em equilíbrio estático depende da
profundidade do ponto, mas não da dimensão horizonta do fluido ou do
recipiente.
1.2 Princípio de Stevin

8. 
 Um mergulhador novato, praticando em uma
piscina, inspira ar suficiente do tanque para expandir
totalmente os pulmões antes de abandonar o tanque
a uma profundidade L e nadar para a superfície. Ele
ignora as instruções e não exala o ar durante a
subida. Ao chegar à superfície, a diferença entre a
pressão externa a que está submetido e a pressão do
ar nos pulmões é 9,3 kPa. De que profundidade
partiu? Que risco possivelmente fatal está correndo?
Exemplo
Pressão barométrica: mergulhador

9. 
 A pressão externa sobre ele está acima do normal e é dada
por
 A diferença entre a pressão mais alta nos pulmões e a
pressão mais baixa no sangue é
 A diferença de pressão de 9,3 kPa é suficiente para
romper os pulmões do mergulhador e forçar a passagem
de ar dos pulmões para a corrente sanguínea, matando o
mergulhador.
Resposta

10. 
 O tubo em forma de U da Figura contém dois
líquidos em equilíbrio estático: no lado direito existe
água de massa específica ρa=998 kg/m3 e no lado
esquerdo existe óleo de massa específica
desconhecida ρx. Os valores das distâncias
especificadas são l=135 mm e d=12,3 mm. Qual é a
massa específica do óleo?
Exemplo
Equilíbrio de pressões em tubo em forma
de U

12. 
 No lado direito, a pressão é dada por
 No lado esquerdo, a pressão é dada por
 Equacionando as duas expressões:
Resposta

13. 
 Uma variação de pressão aplicada a um fluido
incompressível contido em um recipiente é
transmitida integralmente a todas as partes do fluido
Princípio de Pascal

14. 
 Quando um corpo está parcialmente submerso em
um fluido, uma força de empuxo exercida pelo
fluido age sobre o corpo. A força é dirigida para cima
e tem um módulo igual ao peso do fluido deslocado
pelo corpo.
1.3 Princípio de Arquimedes

15. 
 Quando um corpo flutua em um fluido, o módulo da
força gravitacional a que o corpo está submetido é
igual ao peso do fluido deslocado pelo corpo.
 Peso aparente = Peso Real – Módulo da Força de
Empuxo.
Flutuação

16. 
 Na figura, um bloco de massa específica ρ=800
kg/m3 flutua em um fluido de massa específica
ρf=1.200 kg/m3. O bloco tem uma altura H=6 cm.
 (a) Qual é a altura h da parte submersa do bloco?
 (b) Se o bloco for totalmente imerso e depois
liberado, qual será o módulo da sua aceleração?
Exemplo
Flutuação, Empuxo e Massa Específica

18. 
 (a) Como o bloco está em repouso:
 (b) Usando a segunda lei de Newton
Resposta

19. 
Tensão Superficial
 É a força por unidade de comprimento que aparece
no fluido devido à atração das moléculas na
superfície externa de um fluido. É relacionada à
diferença de pressão e aos raios de curvatura da
interface por:
21
11
RR
p
19

20. 
Capilaridade
• Quando um líquido está dentro de um capilar (tubo
muito fino) surgem forças de adesão (devido à
atração das moléculas do líquido com o sólido que
forma o capilar) e forças de coesão (devido à atração
das moléculas do líquido entre si)
• Se as forças de adesão são maiores que as de coesão,
o líquido pode formar um menisco sobre o capilar e
até subir através do capilar.
• Caso contrário, podemos ver o líquido descer pelo
capilar; ficando retido em alguma região dele.
20

21. 
Escoamento Laminar
Escoamento incompressível
Escoamento não viscoso
Escoamento irrotacional
1.4 Dinâmica dos
Fluidos (Fluido Ideal)

22. 
 A velocidade do escoamento aumenta quando a área
da seção reta através do qual o fluido escoa é
reduzida.
Equação da
Continuidade

23. 
 A figura mostra que o jato de água que sai de uma
torneira fica progressivamente mais fino durante a
queda. Essa variação da seção reta horizontal é
característica de todos os jatos de água laminares
(não turbulentos) em queda livre porque a força
gravitacional aumenta a velocidade da água. As
áreas das seções retas indicadas são A0=1,2 cm2 e
A=0,35 cm2. Os dois níveis estão separados por uma
distância vertical h=45 mm. Qual é a vazão da
torneira?
Exemplo
Largura do jato de água de uma torneira

25. 
 De acordo com a Equação da Continuidade
 A água está caindo com aceleração g:
 Eliminando v, nós obtemos a vazão volumétrica
Resposta

26. 
 Se a velocidade de um fluido aumenta enquanto o
fluido se move horizontalmente ao longo de um
linha de reta de fluxo, a pressão do fluido diminui e
vice-versa.
Equação de Bernoulli

27. 
 Um cano horizontal de calibre variável, cuja seção
reta muda de A1=1,2x10-3m2 para A2=A1/2, conduz
um fluxo laminar de etanol, de massa específica
ρ=791 kg/m3. A diferença de pressão entre a parte
larga e parte estreita do cano é 4120 Pa. Qual é a
vazão Rv de etanol?
Exemplo
Aplicação do princípio de Bernoulli a um
cano de calibre variável

28. 
 A vazão no cano é
 A equação de Bernoulli é
 As velocidades são
 Resolvendo para a vazão
Solução

29. 
 No velho Oeste, um bandido atira em uma caixa
d’água sem tampa, abrindo um furo a uma distância
h da superfície da água. Qual é a velocidade v da
água ao sair da caixa d’água?
Exemplo
Aplicação do princípio de Bernoulli a
uma caixa d’água

30. 
 Equação de Bernoulli
 Resolvendo
Solução

31. 
Viscosidade
• É a resistência que o fluido encontra em se mover.
• Pode ser definida (para fluidos Newtonianos)
através do cisalhamento (forças paralelas à seção
transversal por área da seção transversal, τ) e a
componente paralela (à seção transversal) da
velocidade do fluido , u:
• Unidade no S.I. : y
u
sPa
31

32. 
Lei de Poiseulle
 Quando um líquido atravessa um tubo de raio R e
comprimento l, sua vazão é dada em termos da
diferença de pressão entre as extremidades do tubo,
ΔP, e a viscosidade do fluido, η, através de:
l
PR
dt
dV
8
4
32

33. 
Lei de Stokes
 Quando uma partícula esférica é inserida em um
fluido escoando de forma laminar, aparece uma
resistência ao movimento da partícula dentro do
fluido. A força de fricção responsável por isso é dada
em termos da velocidade da partícula, , viscosidade
do fluido, η, e raio da partícula, r; através de:
v

vrF

6
33

34. 
Número de Reynolds
 É uma quantidade que decide se o fluxo do fluido é
laminar (linhas de corrente mantendo paralelismo) e
turbulento (linhas de corrente formando ciclos, nós, etc.):
 D é o comprimento do fluido, v é a velocidade média do
fluido, ρ é a densidade do fluido e η é a viscosidade do
fluido.
 Se Re é maior que 2.400, o fluxo é turbulento. Para Re
menor que 2.000, o fluxo é laminar. Entre 2.000 e 2.400
temos uma situação de transição.
vD
Re
34