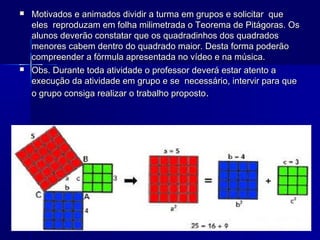
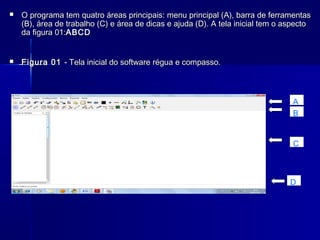
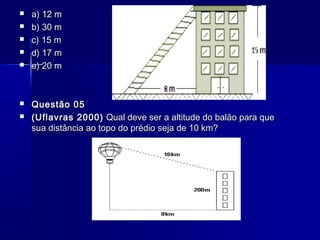
O documento descreve um plano de aulas para ensinar o Teorema de Pitágoras utilizando vídeos, músicas, atividades em grupo, pesquisas na internet e o software Régua e Compasso. As aulas incluem motivação dos alunos, construção e demonstração do teorema com o software, e avaliação com exercícios.

1. O uso do software R.e.C e
outros meios na aprendizagem
do Teorema de Pitágoras
Curso de Informática Educativa I
Cursista: Telma Lúcia da Gama Alvarenga
Tutora: Marina Ribeiro Barros Dias

2. Introdução ao assunto
Despertando a curiosidade


1. 4 aulas ( 200 min ) – 2 aulas na sala de vídeo e 2
aulas no laboratório de informática
A fim de motivar os alunos iniciar a aula utilizando o vídeo
intitulado “O barato de Pitágoras”, disponível em
http://www.youtube.com/watch?v=tKRjJFaKlf4



Após os alunos assistirem o vídeo abrir uma breve discussão
estimulando-os a falarem um pouco sobre o vídeo e, se eles
concordam ou não, quanto a importância dos triângulos.
Fazer as considerações necessários para o fechamento da
discussão.
Logo após apresentar o vídeo da música “Teorema de
Pitágoras, disponível em http://www.youtube.com/watch?v=qjvy2jcbv8w
Disponibilizar a letra da música em folha xerocada e motiválos a cantar!

3. 

Motivados e animados dividir a turma em grupos e solicitar que
eles reproduzam em folha milimetrada o Teorema de Pitágoras. Os
alunos deverão constatar que os quadradinhos dos quadrados
menores cabem dentro do quadrado maior. Desta forma poderão
compreender a fórmula apresentada no vídeo e na música.
Obs. Durante toda atividade o professor deverá estar atento a
execução da atividade em grupo e se necessário, intervir para que
o grupo consiga realizar o trabalho proposto.

4. 
Terminada a atividade solicitar aos alunos que formem duplas e se
dirijam ao laboratório de informática ou a biblioteca da escola onde
deverão fazer pesquisa sobre o tema estudado, bem como trazer
curiosidades sobre a vida de Pitágoras. Deixar a atividade um
pouco livre e logo após sortear três duplas as quais apresentarão o
trabalho pesquisado. Fazer considerações finais caso seja
necessário.

2. 4 aulas ( 200 min ) A segunda etapa do projeto dar-se-a
no laboratório de informática onde caberá o professor apresentar a
interface do software Régua e Compasso utilizando o data-show.
Falar sobre a importância de trabalhar determinados assuntos de
forma dinâmica e que esse software proporcionará essa ação.

Apresentando o software Régua e Compasso.

5. 
O programa tem quatro áreas principais: menu principal (A), barra de ferramentas
(B), área de trabalho (C) e área de dicas e ajuda (D). A tela inicial tem o aspecto
da figura 01:ABCD

Figura 01 - Tela inicial do software régua e compasso.
A
B
C
D

6. 1
7
Ponto .
2
Ocultar objeto .
8
Segmento .
3
Ângulos .
9
Semi Reta .
Mover Ponto .
4
Perpendicular .
10.
Compasso -
Reta .
11.
Ponto Médio -
5
6
Reta Paralela .
Estes são alguns comandos
que se encontram na barra
de ferramentas

7. 




O tutorial bem como algumas atividades que levarão o aluno a se
familiarizar com o software está disponível em:
http://www.es.iff.edu.br/softmat/Softmatoa/Apostilas_de_atividades/apost
3. 2 aulas ( 100 min ) Construção e demonstração do Teorema
de Pitágoras utilizando o software Régua e Compasso
Atividade no laboratório
Assistir o vídeo disponível em
http://www.youtube.com/watch?v=NSn9aCh2qfo
Construir um triângulo retângulo conforme a demonstração feita pelo
tutorial do vídeo.
Salvar a construção.
No menu macros, clique na opção abrir macros.
Clique na ferramenta rodar macro e escolha quadrado, depois
clique nos pontos y e depois em x.

8. 
Repita o mesmo processo para os outros dois lados do triângulo.
Clique com o botão direito do mouse dentro da área de cada um
dos quadrados e escolha a opção mostrar valor.
Com o auxílio da ferramenta mover ponto, mova os pontos x, y e z.

Perguntas:
1) Com a movimentação dos pontos o que acontece com as áreas
dos quadrados?



2) Com o auxilio de uma calculadora, some as áreas dos
quadrados menores, qual foi o valor encontrado?
3) Movimente novamente os pontos x, y e z com o auxílio da
ferramenta mover ponto.
4) Some as áreas dos quadrados menores, qual foi o valor
encontrado?
5) Podemos afirmar que a soma das áreas dos quadrados
menores, é igual a área do quadrado maior?


9. 
6) Construa um triangulo qualquer e monte quadrados em seus
lados. É possível conjecturar a mesma coisa para todos os
triângulos?

7) Baseados nas observações acima, e em todas as atividades
realizadas durante essas semanas é possível afirmar que “o
quadrado da hipotenusa é igual a soma dos quadrados dos catetos
se e somente se o triângulo for retângulo”?

10. 

4. 2 aulas ( 100 min ) – Avaliação
1. Nos telhados de dois edifícios encontram-se duas pombas.




É atirado um pouco de pão para o chão: ambas as pombas se
lançam sobre o pão à mesma velocidade e ambas chegam no
mesmo instante junto do pão.
a) A que distância do edifício B caiu o pão?
b) Qual a altura do edifício A?

11. 






Questão 02
(PUCSP) Dois navios navegavam pelo Oceano Atlântico,
supostamente plano: X, à velocidade constante de 16 milhas por
hora, e Y à velocidade constante de 12 milhas por hora. Sabe-se
que às 15 horas de certo dia Y estava exatamente 72 milhas ao sul
de X e que, a partir de então, Y navegou em linha reta para o leste,
enquanto que X navegou em linha reta para o sul, cada qual
mantendo suas respectivas velocidades. Nessas condições, às 17
horas e 15 minutos do mesmo dia, a distância entre X e Y,
em milhas, era
a) 45
b) 48
c) 50
d) 55
e) 58
Questão 03
A figura mostra um edifício que tem 15 m de altura, com uma escada
colocada a 8 m de sua base ligada ao topo do edifício. O
comprimento dessa escada é de:


12. 






a) 12 m
b) 30 m
c) 15 m
d) 17 m
e) 20 m
Questão 05
(Uflavras 2000) Qual deve ser a altitude do balão para que
sua distância ao topo do prédio seja de 10 km?

13. 




Ficha de avaliação
1. Durante essas semanas estudamos o Teorema de Pitágoras.
Observamos várias maneiras de verificar o teorema,
pesquisamos sobre a vida e curiosidades de Pitágoras e
conhecemos o software régua e compasso. Agora é hora de
avaliarmos nossa caminhada. Abaixo, cite os pontos positivos e
negativos. Escreva qual foi o momento mais interessante das
aulas.
Pontos positivos
_________________________________________________________
_________________________________________________________
__________________________________________
Pontos negativos
_________________________________________________________
_________________________________________________________
__________________________________________
Momento mais interessante
_________________________________________________________
_______________________________________________

14. 













Referências bibliográficas
Disponível em ,
http://www.youtube.com/watch?v=tKRjJFaKlf4
Acessado em 02 out 2013
Disponível em ,
http://www.professores.uff.br/hjbortol/car/
Acessado em 27 set 2013
Disponível em, http://pt.wikipedia.org/wiki/Teorema_de_Pit
%C3%A1goras
Acessado em 02 out 2013
Disponível em,
http://www.youtube.com/watch?v=qjvy2jcbv8w
Acessado em 02 out 2013
Disponível em
http://www.es.iff.edu.br/softmat/Softmatoa/Apostilas_de_atividad
es/apostila_ReC_%202008.pdf
Acessado em 02 out 2013