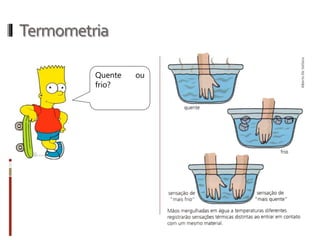
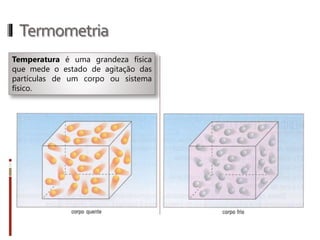
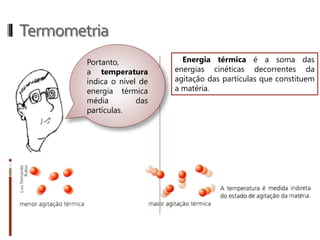
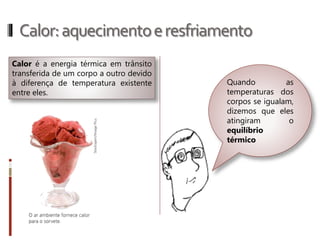
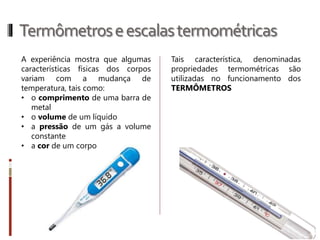
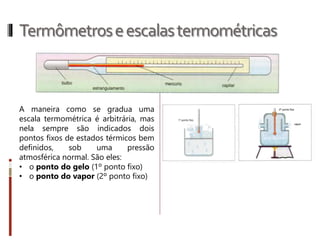
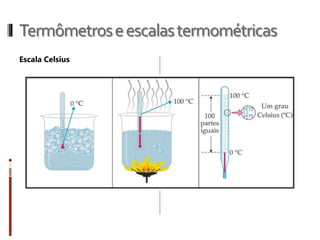
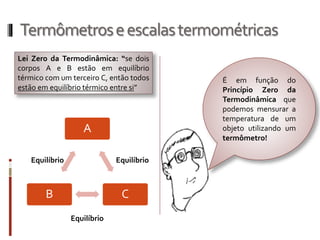
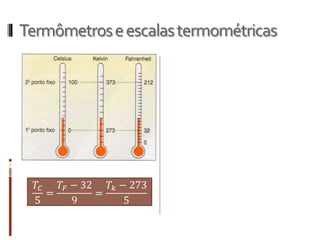
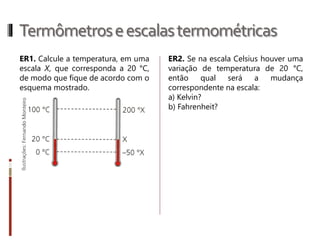
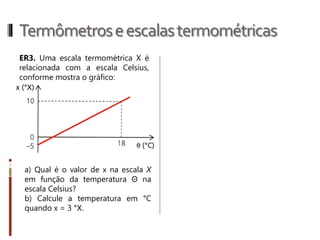
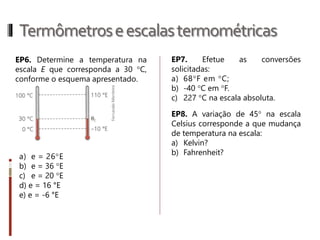
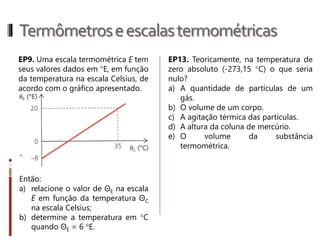
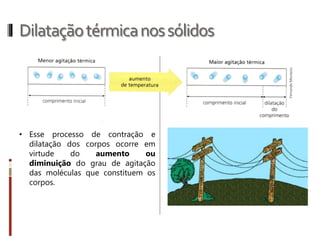
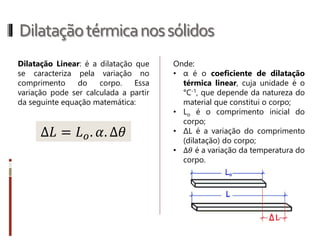
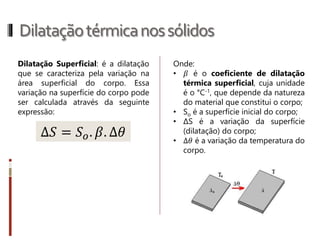
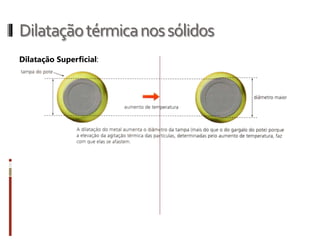
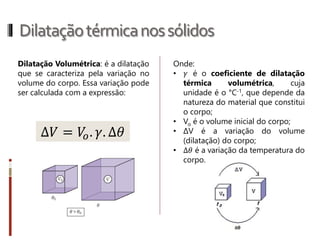
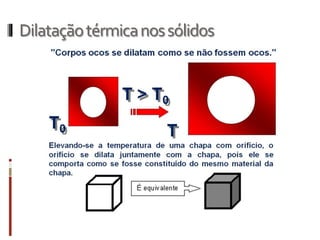
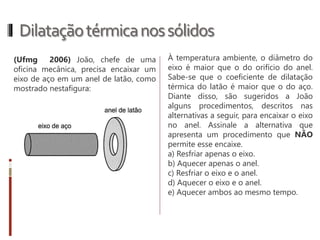
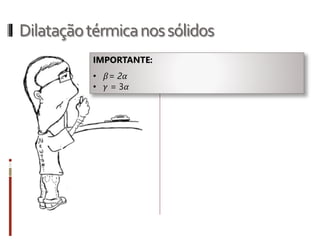
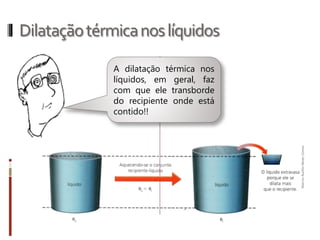
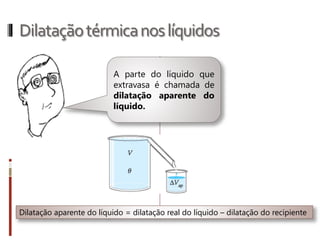
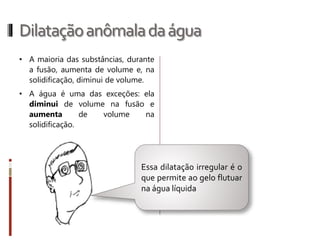
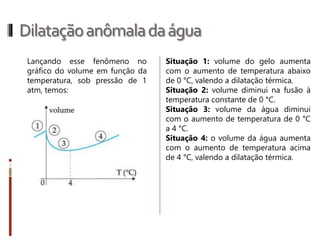
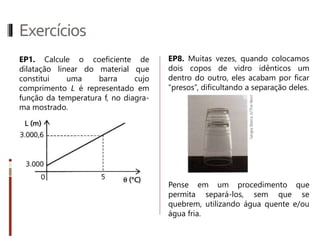
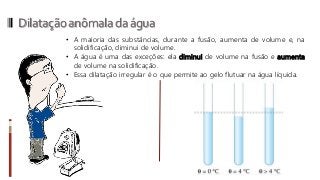
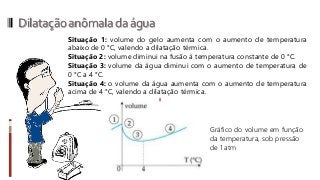
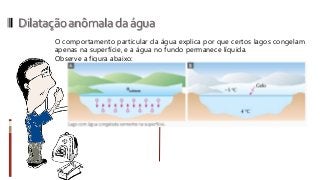
O documento aborda conceitos fundamentais da termologia, incluindo temperatura, calor e estados de agregação da matéria, destacando como a temperatura varia entre escalas termométricas como Celsius, Fahrenheit e Kelvin. Também discute a dilatação térmica em sólidos e líquidos, apresentando fórmulas para calcular variações de comprimento, área e volume em função da temperatura. Além disso, a dilatação anômala da água é mencionada como uma exceção aos padrões de dilatação comuns.

1. Professor MarcoAntonio

2. • observações macroscópicas
• interpretações microscópicas

3. Termologia
Quente ou frio?

4. Termologia
Temperatura é uma grandeza física que mede o estado de agitação das partículas de um
corpo ou sistema físico.

5. Termologia
Portanto,
a temperatura
indica o nível de
energia térmica
média das
partículas.
Energia térmica é a soma das energias
cinéticas decorrentes da agitação das
partículas que constituem a matéria.
Mas cuidado!! Dois corpos podem
apresentar temperaturas iguais (mesmo
grau de agitação térmica), mas possuir
energias térmicas totais diferentes.

6. Calor:aquecimentoeresfriamento
Calor é a energia térmica em trânsito
transferida de um corpo a outro devido à
diferença de temperatura existente entre
eles.
Quando as temperaturas
dos corpos se igualam,
dizemos que eles
atingiram o equilíbrio
térmico!

7. Calor:aquecimentoeresfriamento
Assim, vamos
definir a lei zero da
Termodinâmica:
Portanto, o equilíbrio térmico é caracterizado pela igualdade das temperaturas dos
corpos. Uma vez alcançada essa situação, não há mais transferência de calor entre
eles.
Se dois corpos estão em equilíbrio
térmico com um terceiro, eles estão em
equilíbrio térmico entre si.
Testes Propostos:
Página 24-25 (T1 a T7)

8. Estadosdeagregaçãodamatéria
Como sabemos, a água pode se apresentar como líquido, sólido ou vapor, podendo
passar de uma situação para outra, como mostra a figura 2.

9. Estadosdeagregaçãodamatéria
Sólido, líquido e gasoso são os estados de
agregação da matéria:
• No estado sólido, as forças de coesão
são muito intensas, restringindo o
movimento das moléculas a uma ligeira
vibração em torno de uma posição
média.
As moléculas, fortemente coesas, dispõem-
se com regularidade, geralmente formando
uma rede cristalina. Assim, os sólidos
apresentam forma e volume definidos.

10. Estadosdeagregaçãodamatéria
Sólido, líquido e gasoso são os estados de
agregação da matéria:
• No estado líquido, as distâncias entre as
moléculas são, em média, maiores que
no estado sólido
As forças de coesão ainda são
consideráveis, e há pouca movimentação
das moléculas. Assim, os líquidos
apresentam volume definido, mas sua
forma é variável, adaptando-se à forma
do recipiente que o contém.
• No estado gasoso, as forças de coesão
entre as moléculas têm intensidade
muito pequena, possibilitando uma
movimentação bem mais intensa.
Assim, os gases e vapores não
apresentam forma ou volume definidos.

11. Estadosdeagregaçãodamatéria

13. Termometria
A temperatura é
medida por meio de
aparelhos chamados
de termômetros.

14. Termômetroseescalastermométricas
A experiência mostra que algumas
características físicas dos corpos variam
com a mudança de temperatura, tais
como:
• o comprimento de uma barra de metal
• o volume de um líquido
• a pressão de um gás a volume
constante
• a cor de um corpo
Tais característica, denominadas
propriedades termométricas são utilizadas
no funcionamento dos TERMÔMETROS

15. Termômetroseescalastermométricas
A maneira como se gradua uma escala
termométrica é arbitrária, mas nela
sempre são indicados dois pontos fixos
de estados térmicos bem definidos, sob
uma pressão atmosférica normal. São
eles:
• o ponto do gelo (1º ponto fixo)
• o ponto do vapor (2º ponto fixo)

16. Termômetroseescalastermométricas
As principais escalas termométricas que
iremos estudar são:
• Escala Celsius: atribui o valor de 0°C
para o ponto do gelo e 100°C para o
ponto do vapor. É dividido em cem
partes iguais de 1°C cada.
• Escala Fahrenheit: atribui os valores de
32° F e 212°F para os pontos do gelo e
do vapor. Assim, o termômetro
Fahrenheit pode ser dividido, entre
esses dois pontos fixos, em 180 partes
(212 menos 32) de 1°F cada.
• Escala Kelvin: é conhecida como escala
absoluta, é a única em que o zero
significa total ausência de agitação
térmica.

17. Termômetroseescalastermométricas
Na escala Celsius sobre Kelvin,
verificamos que a temperatura do gelo
fundente, 0o C, equivale a 273 K e, a
ebulição da água a 100°C corresponde ao
valor de 373 K. Portanto, a escala Kelvin
está igualmente dividida em cem partes
de 1 K (um Kelvin) cada uma.
Ainda, o zero absoluto, temperatura na
qual cessa toda a agitação molecular,
mede -273,15o C.

18. Termômetroseescalastermométricas
𝑇𝐶
5
=
𝑇𝐹 − 32
9
=
𝑇𝑘 − 273
5

19. Termômetroseescalastermométricas
1- Um termômetro indica que a
temperatura de uma porção de água é
10ºC. Se fosse usado um termômetro
graduado na escala Fahrenheit, qual seria
a temperatura indicada?
2- Numa cidade da Europa, no decorrer
de um ano, a temperatura mais alta no
verão foi 86ºF. Determine a temperatura,
em graus Celsius, ocorrida naquela
cidade.
3- No ser humano, a temperatura
corpórea pode variar no intervalo de
35ºC a 42ºC.
a) Qual é a variação de temperatura do
corpo humano?
b) Qual seria a variação dessa
temperatura na escala Fahrenheit?
4- Num termômetro digital europeu, lê-
se 14 ºF. Qual será essa temperatura na
escala Celsius?
5- Uma estudante de enfermagem
observa que a temperatura de certo
paciente variou, num período, de 5ºC.
Qual será variação corresponde na escala
Fahrenheit?

20. Variaçãodetemperatura
Considere que a temperatura de um
sistema varie de um valor inicial para
outro final.
Definimos variação de temperatura Δϴ
como sendo a diferença entre a
temperatura final e a inicial:
Agora, considerando que as escala Celsius e
Fahreinheit possuem diferentes divisões,
podemos estabelecer uma relação entre a
variação de temperatura nas duas escalas:
ΔΘ=Θf−Θi
ou

21. Termômetroseescalastermométricas
R.1 A temperatura média do corpo
humano é 36 °C. Determine o valor dessa
temperatura na escala Fahrenheit.
R.2 Dois termômetros, um graduado na
escala Celsius e o outro na escala
Fahrenheit, fornecem a mesma leitura
para a temperatura de um gás. Determine
o valor dessa temperatura.
R.3 Certa escala termométrica adota os
valores -20 e 580, respectivamente, para os
pontos do gelo e do vapor. Determine:
a) a fórmula de conversão entre essa escala
e a escala Celsius;
b) a indicação que nessa escala corresponde
a 20 °C.

22. Termômetroseescalastermométricas
R.4 Uma escala termométrica X
relaciona-se com a escala Celsius,
segundo o gráfico apresentado a seguir,
no qual as ordenadas representam os
valores de ϴX (temperaturas expressas na
escala X) e as abscissas os valores de ϴC
(temperaturas expressas na escala
Celsius).
a) Estabeleça a fórmula de conversão entre
as escalas X e Celsius.
b) Determine a temperatura registrada por
um termômetro graduado na escala X
quando a temperatura for 50 °C.
c) Determine que temperatura registra um
termômetro graduado na escala Celsius para
um sistema em que o termômetro graduado
na escala X registra 10 °X.
d) Há uma temperatura em que os dois
termômetros (graduados na escala X e na
escala Celsius, respectivamente) registram
valores que coincidem numericamente. Qual
é essa temperatura?

23. R.5 Em certo dia, na cidade de Salvador,
o serviço de meteorologia anunciou a
temperatura máxima de 40 °C e a
mínima de 25 °C.
a) Qual é a variação de temperatura entre
os instantes em que foram assinaladas as
temperaturas máxima e mínima?
b) Qual é o valor dessa variação de
temperatura expresso na escala
Fahrenheit?
R.5 Num termômetro de mercúrio, a coluna
líquida apresenta 0,4 cm quando em presença
do gelo em fusão (0 °C) e 20,4 cm em
presença de vapores de água em ebulição
(100 °C). Determine:
a) a função termométrica desse termômetro
na escala Celsius;
b) a temperatura indicada por esse
termômetro quando sua coluna líquida
apresenta 8,4 cm de altura.
Termômetroseescalastermométricas

24. EscalaabsolutaKelvin
A origem da escala Kelvin é o zero
absoluto e a unidade adotada é
o kelvin (símbolo K), cuja extensão é igual
à do grau Celsius (°C). Assim, uma
variação de temperatura de 1 °C
corresponde a uma variação de
temperatura de 1 K.

25. EscalaabsolutaKelvin
R.8 A temperatura corporal humana pode
variar entre 35 °C e 42 °C na escala
Celsius.
a) Determine os valores desses limites na
escala absoluta Kelvin.
b) Calcule a variação de temperatura (nas
escalas Celsius e Kelvin) quando a
temperatura de uma pessoa se altera do
menor para o maior dos valores citados
acima.

27. Dilataçãotérmicanossólidos

28. Dilataçãotérmicanossólidos

29. Dilataçãotérmicanossólidos

30. Dilataçãotérmicanossólidos
Todos os corpos existentes na natureza, sólidos, líquidos ou gasosos,
quando em processo de aquecimento ou resfriamento, ficam sujeitos
à dilatação ou contração térmica.

31. Dilataçãotérmicanossólidos
Esse processo de contração e dilatação
dos corpos ocorre em virtude do
aumento ou diminuição do grau de
agitação das moléculas que constituem
os corpos.

32. Dilataçãotérmicanossólidos
Apesar da dilatação térmica ser sempre uma dilatação volumétrica, pois as
moléculas afastam-se umas das outras em qualquer direção, podemos
analisar a dilatação:
• dilatação linear – aumento de uma das dimensões do
corpo, como o comprimento de uma barra (fig. A);

33. Dilataçãotérmicanossólidos
Apesar da dilatação térmica ser sempre uma dilatação volumétrica, pois as
moléculas afastam-se umas das outras em qualquer direção, podemos
analisar a dilatação:
• dilatação superficial – aumento da área de uma
superfície, como a de uma placa (fig. B);

34. Dilataçãotérmicanossólidos
Apesar da dilatação térmica ser sempre uma dilatação volumétrica, pois as
moléculas afastam-se umas das outras em qualquer direção, podemos
analisar a dilatação:
• dilatação volumétrica – aumento do volume do corpo
(fig. C).

35. Dilataçãotérmicanossólidos
Dilatação Linear: é a dilatação que se
caracteriza pela variação no
comprimento do corpo.
Onde:
• α é o coeficiente de dilatação térmica
linear, cuja unidade é o °C-1, que
depende da natureza do material que
constitui o corpo;
• Lo é o comprimento inicial do corpo;
• ΔL é a variação do comprimento
(dilatação) do corpo;
• Δθ é a variação da temperatura do
corpo.
∆𝐿 = 𝐿 𝑜. 𝛼. Δ𝜃
Essa variação pode ser calculada a partir
da seguinte equação matemática:

36. Dilataçãotérmicanossólidos
R.9 Uma barra apresenta, a 10 °C,
comprimento de 90 m, sendo feita de um
material cujo coeficiente de dilatação linear
médio vale 19.10
-6
ºC
-1
. A barra é aquecida
até 20 °C. Determine:
a) a dilatação ocorrida;
b) a dilatação relativa, expressa em
porcentagem;
c) o comprimento final da barra.
R.11 O gráfico mostra como varia o
comprimento de uma barra metálica em
função da temperatura.
a) Determine o coeficiente de dilatação linear
médio do metal, no intervalo de temperatura
considerado.
b) Considerando que o gráfico continue com
as mesmas características para θ > 40ºC,
determine o comprimento da barra a 70 °C.
Exercícios página 54: 22-23 e 25

37. Dilataçãotérmicanossólidos
Dilatação superficial: é a dilatação que se
caracteriza pela variação na do corpo.
Onde:
• β é o coeficiente de dilatação térmica
superficial, cuja unidade é o °C-1, que
depende da natureza do material que
constitui o corpo;
• So é a superfície (área) inicial do corpo;
• ΔS é a variação da superfície (dilatação)
do corpo;
• Δθ é a variação da temperatura do
corpo.
∆𝑆 = 𝑆 𝑜. 𝛽. Δ𝜃
Essa variação pode ser calculada a partir
da seguinte equação matemática:
𝛽 = 2𝛼

38. Dilataçãotérmicanossólidos
Dilatação superficial

39. Dilataçãotérmicanossólidos
R.13 Uma placa apresenta inicialmente área
de 1 m2 a 0 °C. Ao ser aquecida até 50 °C,
sua área aumenta de 0,8 cm². Determine o
coeficiente de dilatação superficial β e o
coeficiente de dilatação linear médio α do
material que constitui a placa.
Exercícios página 57: 29 e 30

40. Dilataçãotérmicanossólidos
Dilatação volumétrica: é a dilatação que
se caracteriza pela variação no volume
do corpo.
Onde:
• γ é o coeficiente de dilatação térmica
superficial, cuja unidade é o °C-1, que
depende da natureza do material que
constitui o corpo;
• Vo é o volume inicial do corpo;
• ΔV é a variação do volume (dilatação) do
corpo;
• Δθ é a variação da temperatura do
corpo.
∆𝑉 = 𝑉𝑜. 𝛾. Δ𝜃
Essa variação pode ser calculada a partir
da seguinte equação matemática:
γ = 3𝛼

41. Dilataçãotérmicanossólidos
R.15 O coeficiente de dilatação linear médio
de um sólido homogêneo é 12,2.10
-6
ºC
-1
.
Um cubo desse material tem volume de 20
cm³ a 10 °C. Determine:
a) o aumento de volume sofrido pelo cubo
quando sua temperatura se eleva para 40
°C;
b) a dilatação relativa correspondente,
expressa em porcentagem.
R.16 Um tubo de ensaio apresenta, a 0 °C,
um volume interno (limitado pelas paredes)
de 20 cm³. Determine o volume interno
desse tubo a 50 °C. O coeficiente de
dilatação volumétrica médio do vidro é
25.10
-6
ºC
-1
para o intervalo de temperatura
considerado.
Exercícios página 59: 33 e 34

42. Dilataçãotérmicanossólidos

43. Dilataçãotérmicanoslíquidos
A dilatação volumétrica de um líquido segue uma lei idêntica à da
dilatação dos sólidos, válida quando o intervalo de temperatura
considerado não é muito grande. Assim, a variação ΔV do volume
líquido é diretamente proporcional ao volume inicial V0 e à variação
de temperatura ocorrida:
∆𝑉 = 𝑉𝑜. 𝛾. Δ𝜃

44. Dilataçãotérmicanoslíquidos
Como o líquido está contido em um recipiente sólido, que também se dilata,
a medida da dilatação do líquido é calculada indiretamente. Assim, a parte do
líquido que extravasa é chamada de dilatação aparente do líquido.
Observe que, o coeficiente de dilatação aparente de um líquido é
dado pela diferença entre o coeficiente de dilatação real do líquido e
o coeficiente de dilatação volumétrica do recipiente.
𝛾𝑎𝑝 = 𝛾𝑙í𝑞- 𝛾 𝑟𝑒𝑐𝑖𝑝

45. R.17 Um recipiente de vidro de coeficiente
de dilatação linear médio 9.10
-6
ºC
-1
tem
volume de 100 cm³ a 0 °C, estando
completamente cheio com um líquido. Ao
aquecer esse recipiente até 200 °C,
extravasam 5 cm³ de líquido. Determine:
a) o coeficiente de dilatação aparente do
líquido;
b) o coeficiente de dilatação real do líquido.
Exercícios página 62: 36 e 37
Dilataçãotérmicanoslíquidos

46. Dilataçãoanômaladaágua
• A maioria das substâncias, durante a fusão, aumenta de volume e, na
solidificação, diminui de volume.
• A água é uma das exceções: ela diminui de volume na fusão e aumenta
de volume na solidificação.
• Essa dilatação irregular é o que permite ao gelo flutuar na água líquida.

47. Dilataçãoanômaladaágua
Situação 1: volume do gelo aumenta com o aumento de temperatura
abaixo de 0 °C, valendo a dilatação térmica.
Situação 2: volume diminui na fusão à temperatura constante de 0 °C.
Situação 3: volume da água diminui com o aumento de temperatura de
0 °C a 4 °C.
Situação 4: o volume da água aumenta com o aumento de temperatura
acima de 4 °C, valendo a dilatação térmica.
Gráfico do volume em função
da temperatura, sob pressão
de 1 atm

48. Dilataçãoanômaladaágua
O comportamento particular da água explica por que certos lagos congelam
apenas na superfície, e a água no fundo permanece líquida.
Observe a figura abaixo:

49. 1. Com a finalidade de compensar a
dilatação que ocorre nos trilhos de uma
estrada de ferro, é deixado um vão ou
folga de 0,036% do comprimento de cada
barra, à temperatura de 20°C. Calcule o
coeficiente de dilatação linear do ferro, se
aos 50°C as extremidades dos trilhos se
tocam.
2. Uma placa retangular, de vidro comum,
de 50 cm de comprimento e 20 cm de
largura, tem a temperatura elevada de 10
°C até 30 °C. Então, qual será a área final
da superfície dessa placa?
Dado: α = 8.10-6 ºC-1
3. Um bloco cúbico, de vidro comum, de 5
cm de aresta, tem sua temperatura elevada
de 27 °C até 57 °C. Calcule o volume final
desse cubo. Dado: α = 8.10-6 ºC-1
4. Um objeto tem uma cavidade cuja
capacidade é de 8 mL, a 20 °C. Ele é aquecido
até 120 °C. O material homogéneo e isótropo
desse objeto tem coeficiente de dilatação
linear igual a 2.10-5 °C-1. Qual é, nessas
condições, a variação da capacidade volu-
métrica da cavidade?

50. 1. (PUC-RJ) Uma porca está muito
apertada no parafuso. O que você deve
fazer para afrouxá-la?
a) É indiferente esfriar ou esquentar a
porca.
b) Esfriar a porca.
c) Esquentar a porca.
d) É indiferente esfriar ou esquentar o
parafuso.
e) Esquentar o parafuso.
2. Muitas vezes, quando colocamos dois
copos de vidro idênticos um dentro do outro,
eles acabam por ficar “presos”, dificultando a
separação deles.
Pense em um procedimento que permita
separá-los, sem que se quebrem, utilizando
água quente e/ou água fria.

51. 3. (Ufmg) João, chefe de uma oficina
mecânica, precisa encaixar um eixo de
aço em um anel de latão, como
mostrado nesta figura:
À temperatura ambiente, o diâmetro do eixo
é maior que o do orifício do anel. Sabe-se
que o coeficiente de dilatação térmica do
latão é maior que o do aço. Diante disso,
são sugeridos a João alguns procedimentos,
descritos nas alternativas a seguir, para
encaixar o eixo no anel. Assinale a
alternativa que apresenta um procedimento
que NÃO permite esse encaixe.
a) Resfriar apenas o eixo.
b) Aquecer apenas o anel.
c) Resfriar o eixo e o anel.
d) Aquecer o eixo e o anel.
e) Aquecer ambos ao mesmo tempo.