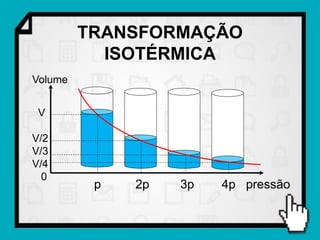
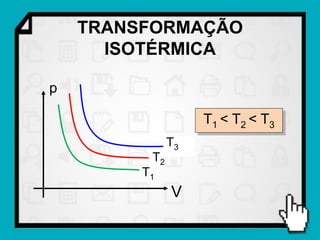
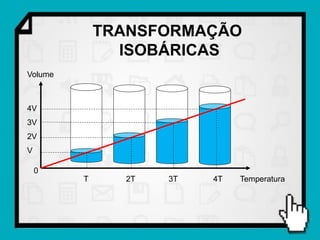
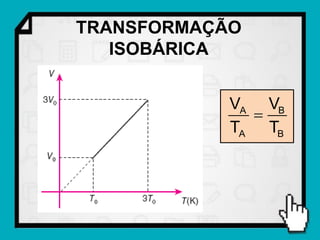
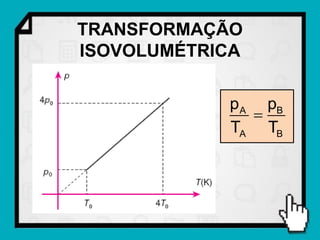
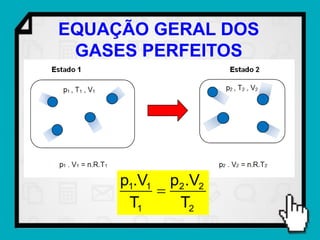
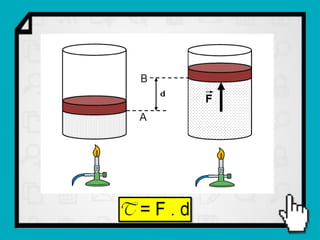
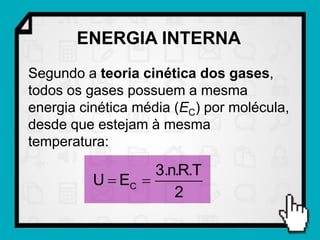
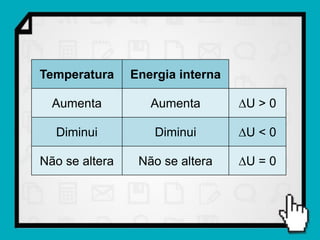
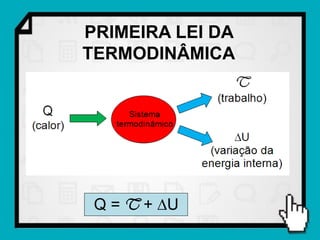
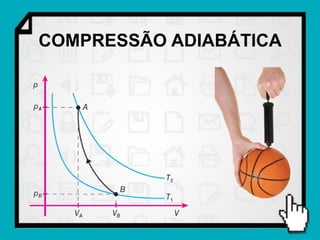
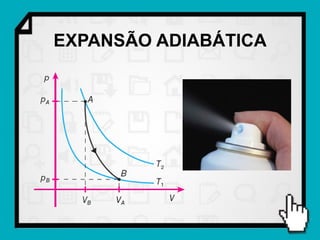
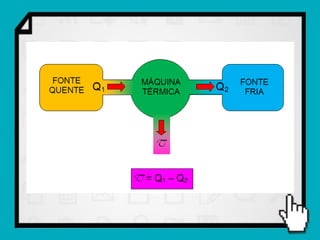
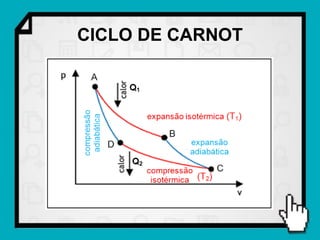
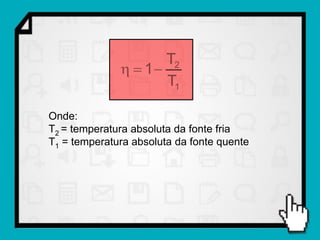
Este documento resume os principais conceitos da termodinâmica, incluindo: (1) as variáveis de estado de um gás, como pressão, volume e temperatura; (2) as leis dos gases ideais e transformações gasosas; e (3) a primeira e segunda lei da termodinâmica.

1. FÍSICA
Prof. Amilcar

2. TERMODINÂMICA

3. ESTUDO DOS GASES

4. O ESTADO GASOSO
Pressão (p)
Variáveis de
um gás Volume (V)
Temperatura (T)

5. Pressão: contém é devido a inúmeras
colisões entre as moléculas que o compõem e
as paredes do recipiente.
Volume: O gás não possui forma e volume
definidos. O volume que um gás possui é igual
ao volume do recipiente ocupado por ele.
1 m³ = 10³ L

6. Temperatura: Mede o estado de
agitação das moléculas do corpo. No estudo
dos gases perfeitos a temperatura deve estar
na escala Kelvin onde:
T = c + 273

7. EQUAÇÃO DE CLAPEYRON
As variáveis de estado pressão (p), volume
(V ) e temperatura (T ) de uma massa de
gás ideal contendo n mols de gás estão
relacionadas pela equação de estado dos
gases perfeitos (ou ideais):
pV=nRT

8. Um cilindro metálico de 41 litros contém
argônio (massa de um mol = 40 g) sob
pressão de 90 atm à temperatura de 27 °C.
Qual a massa de argônio no interior desse
cilindro?
Resolução:
Dados fornecidos no texto:
V = 41 L
M = 40 g
p = 90 atm
T = 27 °C = 300 K

9. Dados fornecidos: V = 41 L M = 40 g
p = 90 atm T = 27 °C = 300 K
Primeiro determina-se Agora se calcula a
o número de mols massa do gás:
do argônio: m m
n  150 
M 40
p.V=n.R.T
90 . 41 = n . 0,082 . 300 m  6000 g  6 kg
3690 = 24,6 n
n = 150 mols

10. A transformação gasosa ocorre
quando pelo menos uma das
variáveis de estado se modifica.

11. TRANSFORMAÇÕES GASOSAS
Isotérmicas: a temperatura do sistema
permanece constante.
Isobáricas: a pressão é mantida
constante.
Isovolumétricas (isométricas ou
isocóricas): o volume permanece
constante.

12. TRANSFORMAÇÃO
ISOTÉRMICA
Lei de Boyle: a pressão exercida por um gás
ideal é inversamente proporcional ao seu
volume.
Considerando o estado inicial A e final B de
um gás ideal sofrendo uma transformação
isotérmica, tem-se:
pA  VA = pB  VB

13. TRANSFORMAÇÃO
ISOTÉRMICA
Volume
V
V/2
V/3
V/4
0
p 2p 3p 4p pressão

14. TRANSFORMAÇÃO
ISOTÉRMICA
p
T1 < T2 < T3
T3
T2
T1
V

15. TRANSFORMAÇÃO
ISOBÁRICA
Lei de Charles e Gay-Lussac: o volume ocupado por
um gás é diretamente proporcional a sua temperatura
absoluta (em kelvins).
Considerando o estado inicial A e final B de um gás
ideal sofrendo uma transformação isobárica, tem-se:
VA VB

TA TB

16. TRANSFORMAÇÃO
ISOBÁRICAS
Volume
4V
3V
2V
V
0
T 2T 3T 4T Temperatura

17. TRANSFORMAÇÃO
ISOBÁRICA
VA VB

TA TB

18. TRANSFORMAÇÃO
ISOVOLUMÉTRICA
Lei de Charles para transformações a volume
constante: a pressão do gás é diretamente
proporcional a sua temperatura absoluta (em kelvins).
Considerando o estado inicial A e final B de um gás
ideal sofrendo uma transformação isobárica, tem-se:
p A pB

TA TB

19. TRANSFORMAÇÃO
ISOVOLUMÉTRICA
p A pB

TA TB

20. EQUAÇÃO GERAL DE UM
GÁS PERFEITO

21. EQUAÇÃO GERAL DOS
GASES PERFEITOS
p1.V1 p2 .V2

T1 T2

22. Um gás perfeito é mantido em um cilindro
fechado por um pistão. Em um estado A, as
suas variáveis são: pA = 2,0 atm; VA = 0,90 L;
TA = 27ºC. Em outro estado B, a temperatura é
TB = 127ºC e a pressão é pB = 1,5 atm.
Nessas condições, qual o volume VB, em
litros?

23. Resolução:
pA .VA pB .VB

Dados fornecidos: TA TB
pA = 2 atm
VA = 0,90 L 2. 0,90 1 . VB
,5

TA = 27 °C = 300 K 300 400
pB = 1,5 atm VB  1 L
,6
VB = ?
TB = 1,27 °C = 400 K

24. TRABALHO EM UMA
TRANSFORMAÇÃO GASOSA
Faísca
elétrica
Entrada de
mistura gasosa Saída de gases
(ar + combustível) após combustão
Câmara de
Pistão
combustão
(cilindro)

27. T = p . V
Válida para pressão
constante.

28. Da expressão do trabalho, verifica-se
que ele pode ser positivo, negativo ou
nulo.
Trabalho feito
Volume Trabalho
pelo gás
Aumenta Realizado (+)
Diminui Recebido (–)
Constante Não existente Nulo

29. TRABALHO COM
PRESSÃO VARIÁVEL
pressão
p2 B
N
Área = T
A
p1
volume
V1 V2

30. Certa massa gasosa sofre a transformação
AB indicada no diagrama.
5 2
p (10 N/m )
A
3
2
1 B
-3 3
0 1 2 3 V (10 m )
Qual o trabalho realizado pelo gás na
transformação AB ?

31. O trabalho na transformação AB é dado pela
área descrita no diagrama:
5
p(10 N/m )
2 T = Área
 3.105  1.105 
3 A T =   .2.103
 2 
2
1 B T = 4 . 102 J
-3 3
0 1 2 3 V(10 m )

32. TRANSFORMAÇÃO CÍCLICA
pressão A  posição inicial
p2 B
A
p1 C
volume
V1 V2

33. pressão
pressão
p2 B p2 B
TAB = A1 TBC = 0
A
p1 p1 C
Área 1
volume volume
V1 V2 V1 V2
pressão
pressão
p2 B
p2 N
Área = T
TCA = - A2
A
A p1 C
p1 C
Área 2
volume V1 V2 volume
V1 V2

34. Em toda transformação cíclica
representada no diagrama p x V, o
trabalho realizado é fornecido pela área
do ciclo.
- sentido horário  o gás realiza
trabalho (T > 0)
- sentido anti-horário  o gás recebe
trabalho (T < 0)

35. Um gás ideal sofre transformações segundo
o ciclo dado no esquema p x V a seguir.
O trabalho no ciclo é
numericamente igual à
área interna do diagrama e
como o ciclo é anti-horário
o trabalho é negativo:
T = Área
4.106. 2.105
T=-
Qual o trabalho total no 2
ciclo ABCA ? T = - 4 . 10-1 J
T = - 0,4 J

36. ENERGIA INTERNA
É resultante da soma de várias energias,
como as de translação, de rotação e de
vibração, a potencial e a energia associada
à agitação térmica das moléculas do gás.
Rotação
Vibração
Translação

37. ENERGIA INTERNA
Segundo a teoria cinética dos gases,
todos os gases possuem a mesma
energia cinética média (EC) por molécula,
desde que estejam à mesma
temperatura:
3.n.R.T
U  EC 
2

38. Temperatura Energia interna
Aumenta Aumenta U > 0
Diminui Diminui U < 0
Não se altera Não se altera U = 0

39. PRIMEIRA LEI DA
TERMODINÂMICA
Q = T + U

40. Um corpo recebe 180 Joules de calor de um
outro corpo e rejeita 40 Joules para o ambiente.
Simultaneamente, o corpo realiza um trabalho de
150 Joules. Qual foi a variação da energia interna
do sistema termodinâmico?
O sistema termodinâmico recebeu uma quantidade de
calor efetiva de Q = 180 – 40 = 140 J e realizou um
trabalho de 150 J. Assim, tem-se:
Q = T + U
140 = 150 + U
U = - 10 J

41. APLICAÇÕES DA PRIMEIRA
LEI DA TERMODINÂMICA
Transformação adiabática
Não ocorrem trocas de
calor entre o sistema e
o meio externo (Q = 0).

42. COMPRESSÃO ADIABÁTICA

43. EXPANSÃO ADIABÁTICA

44. SEGUNDA LEI DA
TERMODINÂMICA

45. É impossível a construção de uma
máquina que, operando em um
ciclo termodinâmico, converta toda
a quantidade de calor recebido em
trabalho.

47. Rendimento de uma máquina
térmica
O rendimento de uma máquina térmica é a
razão entre a energia útil (trabalho) pela
energia total (quantidade de calor da fonte
quente) que a máquina recebe para realizar
trabalho.
energia útil
 
energia total

48. CICLO DE CARNOT

49. T2
  1
T1
Onde:
T2 = temperatura absoluta da fonte fria
T1 = temperatura absoluta da fonte quente

50. Uma máquina térmica, operando em um ciclo
de Carnot, trabalha entre as temperaturas de –
73ºC e 227ºC. Em cada ciclo, a máquina recebe
500 J de calor da fonte quente. Analise as
seguintes afirmativas:
I. O rendimento dessa máquina é de 40%.
II. O trabalho realizado pela máquina é de 300 J.
III. O calor rejeitado, por ciclo, para a fonte fria é
de 200 J.
Quais afirmações são corretas?

51. Resolução:
I. O rendimento é dado por:
T2
 1
 273  73   1  200
  1
T1  273  227  500
  0,6 ou 60%

52. II. Como o calor recebido é de 500 J, tem-
se:
  T = 300 J

53. III. O calor rejeitado é:
T = Q1 – Q2
300 = 500 - Q2
Q2 = 200 J