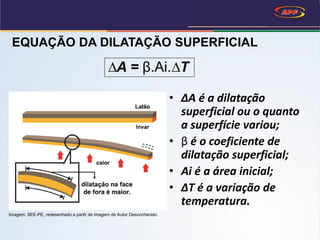
1) O documento discute o fenômeno da dilatação térmica em sólidos, explicando como o aumento da temperatura causa a expansão das dimensões de um corpo em uma, duas ou três dimensões. 2) Apresenta as equações que descrevem a dilatação linear, superficial e volumétrica em função do comprimento/área/volume inicial, variação de temperatura e coeficiente de dilatação. 3) Aplica essas equações para calcular a dilatação em três exemplos numéricos.

1. Profª: Daniela Fontana Almenara
Disciplina: Física
Turma: 2º Ano do Ensino médio
Dilatação Térmica dos Sólidos

2. Expansão das Moléculas
• Temperatura: é a medida do grau de agitação das moléculas;
• Calor: é a troca de energia causada exclusivamente por uma
diferença de temperatura.
É importante que saibamos o que são temperatura e calor.
Imagem: SEE-PE

3. Em física, dilatação térmica é o nome que se
dá ao crescimento das dimensões de um corpo,
ocasionado pelo aumento de sua temperatura.
Dilatação Térmica
Definição

4. Para pensar melhor...
• Como facilitar a abertura da tampa de um vidro
de azeitonas ?
• A tampa de metal e o vidro sofrerão alterações
quando aquecidas?
• Como esse fenômeno pode ser explicado
fisicamente?

5. Você já observou os trilhos em uma estrada de
ferro?
Imagem:Powerkites16/classicalmusic.mzrt@gmail.com/PublicDomain.

6. Os fios de telefone ou luz,
expostos ao Sol, variam
suas temperaturas, fazendo
com que o fio se estenda
de um comprimento inicial
(Lo) para um comprimento
final (L), aumentando assim
sua curvatura.
Imagem: Hugh Venables /
Creative Commons Attribution-Share Alike 2.0 Generic.

7. Ocorre quando o corpo sofre expansão em uma dimensão
A dilatação do fio
depende de três fatores:
• da substância da qual
é feito o fio;
• da variação de
temperatura sofrida pelo
fio;
• do comprimento inicial
do fio.
Dilatação Linear
Imagem: SEE-PE, redesenhado a partir de imagem de Autor
Desconhecido.

8. EQUAÇÃO DA DILATAÇÃO LINEAR
∆L = Lo.α.∆T
Imagem: SEE-PE, redesenhado a partir de imagem de Autor Desconhecido.

9. • ∆L é variação de comprimento do fio, ou seja, ∆L = Lf – Lo;
• Lo é o comprimento inicial;
• Lf é o comprimento final;
• α é o coeficiente de dilatação linear, uma característica da
substância. Sua unidade é o °C-1;
• ∆T é a variação de temperatura, ou seja, ∆T = Tf - To, onde To
representa a temperatura inicial do fio e Tf a temperatura
final.

10. • Há corpos que
podem ser
considerados
bidimensionais,
pois sua terceira
dimensão é
desprezível, frente
às outras duas,
por exemplo, uma
chapa.
A expansão ocorre nas suas
duas dimensões lineares, ou
seja, na área total do corpo.
Dilatação Superficial
Imagem: SEE-PE, redesenhado a partir de imagem de Autor Desconhecido.

11. Vemos uma chapa retangular que, ao ser
aquecida, teve toda a sua superfície
aumentada, passando de uma área inicial a
uma área final. Ou seja, a variação da área de
superfície S pode ser escrita por:
∆A= A f – A 0
Imagem: SEE-PE, redesenhado a partir de imagem
de Autor Desconhecido.

12. A dilatação superficial, analogamente à dilatação
linear, depende:
• da variação de temperatura sofrida pelo corpo;
• da área inicial;
• do material do qual é feito o corpo. O coeficiente
utilizado neste caso, é o de dilatação superficial β,
que equivale a duas vezes o coeficiente de dilatação
linear, isto é: 𝛽 = 2𝛼. Sua unidade também é o °C-1 .

13. • ∆A é a dilatação
superficial ou o quanto
a superfície variou;
• β é o coeficiente de
dilatação superficial;
• Ai é a área inicial;
• ∆T é a variação de
temperatura.
∆A = β.Ai.∆T
EQUAÇÃO DA DILATAÇÃO SUPERFICIAL
Imagem: SEE-PE, redesenhado a partir de imagem de Autor Desconhecido.

14. A grande maioria dos corpos sólidos possui três
dimensões: altura, comprimento e espessura.
Quando aquecido, o sólido sofre expansão em
cada uma delas, resultando em um aumento no
volume total do corpo.
Dilatação Volumétrica
Imagem: SEE-PE, redesenhado a partir de
imagem de Autor Desconhecido.

15. EQUAÇÃO DA DILATAÇÃO VOLUMÉTRICA
De forma similar aos casos anteriores, temos a proporcionalidade entre:
• variação da dimensão;
• dimensão inicial;
• variação da temperatura.
Adicionando-se um coeficiente que depende do material do qual o sólido
é formado, garantimos a relação entre os termos da equação da
dilatação volumétrica .
Imagem:SEE-PE,redesenhado
apartirdeimagemdeAutor
Desconhecido.

16. Onde:
• ΔV = Vf – V0 é a variação do volume;
• V0 é o volume inicial;
• ΔT = T – To é a variação da temperatura;
• γ é o coeficiente de dilatação volumétrico;
γ = β = 3α para uma mesma substância. Sua
unidade também é o °C-1.
ΔV= γ .V 0 . ΔT
Assim, obtém-se:

17. 1º Exemplo
• O comprimento de um fio de alumínio é de 40
m a 20 𝑜
𝐶. Sabendo-se que o fio é aquecido
até 60 𝑜
𝐶 e que o coeficiente de dilatação
linear do alumínio é de 24. 10−6 𝑜
𝐶−1
,
determinar:
a) A dilatação do fio;
b) O comprimento final do fio.

18. • Uma placa retangular de alumínio tem 10 cm
de largura e 40 cm de comprimento, à
temperatura de 20 𝑜
𝐶. Essa placa é colocada
num ambiente cuja temperatura é de 50 𝑜
𝐶.
Sabendo-se que 𝛽 𝑎𝑙 = 46. 10−6 𝑜
𝐶−1
,
calcular:
a) A dilatação superficial da placa;
b) A área da placa nesse ambiente.
2º Exemplo

19. • Um paralelepípedo a 100
𝐶 possui dimensões
iguais a 10 cm x 20 cm x 30 cm, sendo
constituído de um material cujo coeficiente de
dilatação térmica linear é 8,0 . 10−6 𝑜
𝐶−1
.
Determinar o acréscimo de volume quando
sua temperatura aumenta para 1100
𝐶.
3º Exemplo