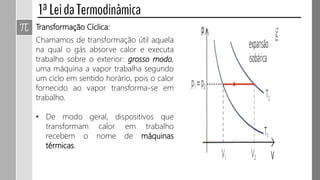
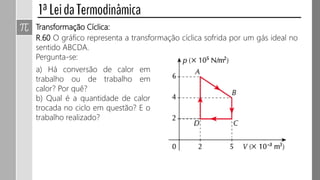
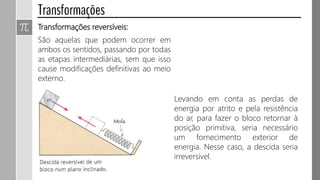
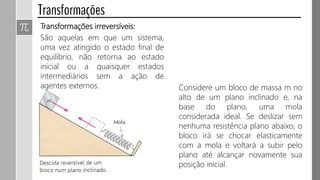
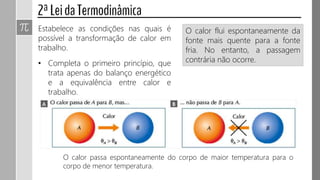
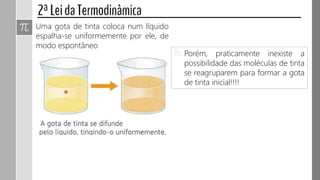
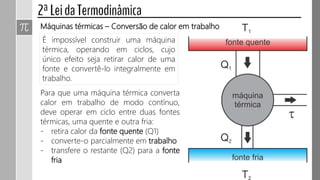
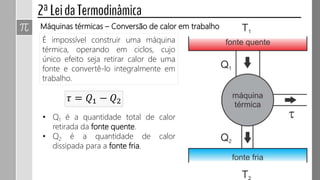
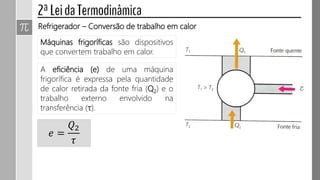
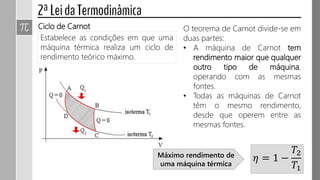
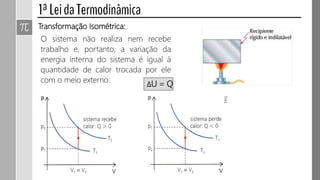
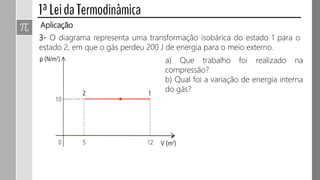
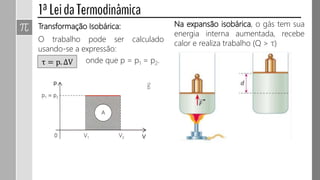
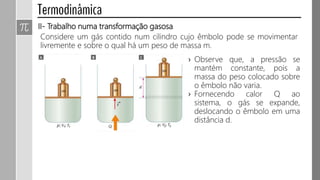
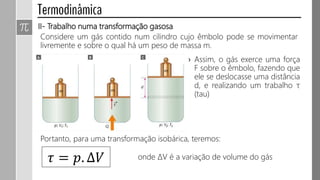
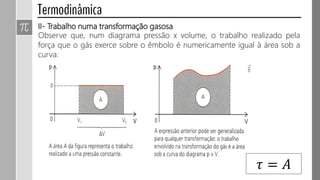
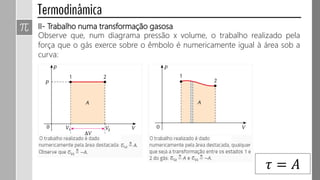
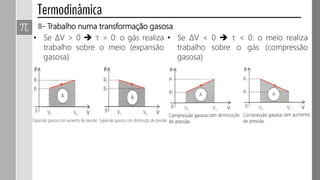
O documento descreve conceitos fundamentais da termodinâmica, incluindo: 1) Termodinâmica estuda as transformações entre calor e trabalho. 2) Sistemas podem ser isolados, fechados, abertos ou adiabáticos. 3) O trabalho realizado em uma transformação gasosa depende da variação de volume do gás.

2. › Termodinâmica é o estudo das transformações entre calor e trabalho.

3. › Termodinâmica é o estudo das
transformações entre calor e
trabalho.
I- Conceitos-chave:
- Calor: energia térmica em
trânsito de um corpo para outro
em razão da diferença de
temperatura entre eles.
- Trabalho: energia em trânsito
entre dois corpos devido à ação de
uma força.
- Sistema: toda região do espaço
que é objeto de estudo.
Do ponto de vista das trocas de
calor, um sistema pode ser:
• Isolado: não troca energia nem
matéria com o meio externo. Ex:
Garrafa térmica.
• Fechado: troca energia, mas não
matéria com o meio externo. Ex:
latinha de refrigerante.
• Aberto: troca energia e /ou matéria
com o meio externo. Ex: a mesma
latinha de refrigerante, agora aberta.
• Termicamente isolado (adiabático):
não troca calor com a vizinhança. As
paredes de um recipiente
termicamente isolado são chamadas
de adiabáticas. Ex: paredes de uma
garrafa térmica.

4. II- Trabalho numa transformação gasosa
Considere um gás contido num cilindro cujo êmbolo pode se movimentar
livremente e sobre o qual há um peso de massa m.
› Observe que, a pressão se
mantém constante, pois a
massa do peso colocado sobre
o êmbolo não varia.
› Fornecendo calor Q ao
sistema, o gás se expande,
deslocando o êmbolo em uma
distância d.

5. II- Trabalho numa transformação gasosa
Considere um gás contido num cilindro cujo êmbolo pode se movimentar
livremente e sobre o qual há um peso de massa m.
› Assim, o gás exerce uma força
F sobre o êmbolo, fazendo que
ele se deslocasse uma distância
d, e realizando um trabalho τ
(tau)
𝜏 = 𝑝. ∆𝑉
Portanto, para uma transformação isobárica, teremos:
onde ΔV é a variação de volume do gás

6. II- Trabalho numa transformação gasosa
O trabalho é uma grandeza escalar que assume o mesmo sinal da variação
de volume, uma vez que a pressão p é sempre positiva. Assim:
 Numa expansão, a variação de volume é positiva e, portanto, o trabalho
realizado é positivo.
 Numa compressão, a variação de volume é negativa e, portanto, o
trabalho realizado é negativo.
 Em uma transformação que ocorre sem variação de volume não há
realização de trabalho.
Resumidamente:

7. II- Trabalho numa transformação gasosa
Observe que, num diagrama pressão x volume, o trabalho realizado pela
força que o gás exerce sobre o êmbolo é numericamente igual à área sob a
curva:
𝜏 = 𝐴

8. II- Trabalho numa transformação gasosa
Observe que, num diagrama pressão x volume, o trabalho realizado pela
força que o gás exerce sobre o êmbolo é numericamente igual à área sob a
curva:
𝜏 = 𝐴

9. • Se ∆V > 0  τ > 0: o gás realiza
trabalho sobre o meio (expansão
gasosa)
• Se ∆V < 0  τ < 0: o meio realiza
trabalho sobre o gás (compressão
gasosa)
II- Trabalho numa transformação gasosa

10. II- Trabalho numa transformação gasosa
• Se ∆V = 0  τ = 0: o sistema não
troca trabalho (transformação
isométrica = o volume não se
altera)

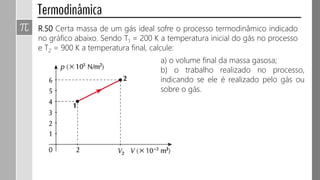
11. R.49 Cinco mols de um gás ideal se encontram à temperatura de 600 K,
ocupando um volume de 0,5 m³. Mediante um processo isobárico, o gás é
submetido à transformação indicada no gráfico.
a) Determine a pressão exercida pelo gás
durante o processo.
b) Qual é a temperatura final do gás?
c) Calcule o trabalho realizado na
transformação, indicando como esse
cálculo pode ser feito por meio do gráfico.
d) O trabalho nesse processo isobárico é
realizado pelo gás ou sobre o gás?
Explique.
[Dado: R=8,31 J/(mol.K)]

12. R.50 Certa massa de um gás ideal sofre o processo termodinâmico indicado
no gráfico abaixo. Sendo T1 = 200 K a temperatura inicial do gás no processo
e T2 = 900 K a temperatura final, calcule:
a) o volume final da massa gasosa;
b) o trabalho realizado no processo,
indicando se ele é realizado pelo gás ou
sobre o gás.

13. III- Energia interna:
 A energia total de um sistema é composta de duas parcelas: a energia
externa e a energia interna.
 A energia interna do sistema relaciona-se com suas condições intrínsecas,
como a energia térmica, associada ao movimento de agitação térmica das
moléculas.
 Na prática não se mede
diretamente a energia interna
U do sistema, no entanto,
para os gases ideais
monoatômicos, vamos
determinar a variação da
energia interna ΔU, por meio
variação da energia cinética
de translação das moléculas
que constituem o sistema.

14. III- Energia interna:
É a soma das energias cinéticas médias de todas as moléculas de um gás
perfeito e é função exclusiva de sua temperatura.
∆𝑈 =
3
2
𝑛. 𝑅. 𝑇
Onde:
• ∆U é a variação da energia interna associada
à transformação
• n é o número de mols de partículas do gás.
Fazendo m = massa de gás e M = massa
molecular, temos que n é dado pela
expressão:
n=
m
M
• R é a constante universal dos gases ideais:
R = 0,082 atm.L/mol.K
• T é a temperatura absoluta (K)

16. Quando um sistema (gás) recebe uma determinada quantidade de calor (Q),
sofre um aumento de sua energia interna (∆U) e, consequentemente, um
aumento de temperatura (∆T):
• Se ∆T > 0  ∆U > 0: a energia interna aumenta.
• Se ∆T < 0  ∆U < 0: a energia interna diminui.
• Se ∆T = 0  ∆U = 0: a energia interna não varia.
III- Energia interna:
A Energia interna de uma certa massa de gás ideal é função exclusiva de sua
temperatura

18. Quando fornecemos a um sistema certa quantidade de energia Q, esta
energia pode ser usada de duas maneiras:
1. Uma parte da energia pode ser
usada para o sistema realizar
um trabalho (𝜏), expandindo-se ou
contraindo-se.
2. A outra parte pode ser absorvida
pelo sistema, virando energia
interna, ou seja, essa outra parte de
energia é igual à variação de
energia (ΔU) do sistema.
Resumidamente: num processo
termodinâmico sofrido por um gás, há
dois tipos de trocas energéticas com o
meio exterior: o calor trocado Q e o
trabalho realizado τ. Veja o exemplo:
∆𝑈 = 𝑄 − 𝜏

19. Definição: a variação de energia interna ΔU de um sistema é igual à diferença
entre o calor Q trocado com o meio externo e o trabalho τ por ele realizado
durante uma transformação.
∆𝑈 = 𝑄 − 𝜏
A primeira lei da Termodinâmica é uma reafirmação do princípio da
conservação da energia e é válida para qualquer processo termodinâmico
natural que envolva trocas energéticas.

20. Resumidamente, teremos que:
Quantidadedecalortrocadocomomeio Q > 0 (positivo) o gás recebeu calor.
Q < 0 (negativo) o gás perdeu calor.
Q = 0 (nulo) o gás não trocou calor com o meio exterior
(transformação adiabática) todo o trabalho trocado
converteu-se em energia interna.

21. Resumidamente, teremos que:
Variaçãodaenergiainternadogás
ΔU > 0 (positivo) a energia interna aumentou, portanto,
sua temperatura aumentou
ΔU < 0 (negativo) a energia interna diminuiu, portanto, sua
temperatura diminuiu
ΔU = 0 (nulo) o processo é isotérmico, qualquer que tenha
sido a troca com o exterior, a temperatura manteve-se
constante.

22. Aplicação
1- Ao receber uma quantidade de calor Q=50J, um gás realiza um trabalho
igual a 12J, sabendo que a Energia interna do sistema antes de receber calor
era U=100J, qual será esta energia após o recebimento?
2- Certa massa de gás perfeito recebeu 300 J de energia do meio exterior e
realizou um trabalho de 500 J. Nessas condições, responda:
a) qual foi a variação de energia interna sofrida pelo gás?
b) a temperatura do sistema aumentou ou diminuiu nesse processo?
Justifique.

23. Aplicação
3- O diagrama representa uma transformação isobárica do estado 1 para o
estado 2, em que o gás perdeu 200 J de energia para o meio externo.
a) Que trabalho foi realizado na
compressão?
b) Qual foi a variação de energia interna
do gás?

24. 4- O diagrama mostra a transformação de uma massa gasosa do estado X
para o estado Y.
a) Determine o módulo do trabalho
realizado sobre o gás.
b) Sabendo-se que a temperatura inicial
do gás era de 600 K, qual sua
temperatura final.
c) O trabalho foi realizado pelo gás ou
sobre o gás? Justifique.

25. R.51 Seis mols de um gás ideal monoatômico sofrem o processo
termodinâmico AB indicado no gráfico. Sendo R = 8,31 J/(mol.K), determine:
a) as temperaturas inicial (TA) e final (TB) do
gás;
b) a variação de energia interna do gás no
processo AB;
c) o trabalho realizado pelo gás ao passar do
estado A para o estado B;
d) a quantidade de calor trocada pelo gás na
transformação de A para B.

26. Transformação Isotérmica:
Como não há variação de temperatura
(ΔU = 0), a quantidade de calor trocada
pelo sistema com o exterior converte-se
integralmente em trabalho:
Q = τ
Na expansão isotérmica, o gás, sem
variar sua energia interna, tem a pressão
reduzida, recebe calor e realiza trabalho

27. Aplicação:
R.52 Numa transformação isotérmica de um gás ideal monoatômico, o
produto pV é constante e vale 33.240 J. A constante dos gases ideais é R =
8,31 J(mol.K) e o número de mols do gás é 5 mol. Durante o processo, o gás
recebe 2.000 J de calor do meio exterior. Determine:
a) se o gás está sofrendo expansão ou compressão;
b) a temperatura do processo;
c) a variação da energia interna do gás;
d) o trabalho realizado na transformação.

28. Transformação Isobárica:
O trabalho pode ser calculado
usando-se a expressão:
τ = p. ∆V onde que p = p1 = p2.
Na expansão isobárica, o gás tem sua
energia interna aumentada, recebe
calor e realiza trabalho (Q > τ)

29. Transformação Isobárica:
O trabalho pode ser calculado
usando-se a expressão:
τ = p. ∆V onde que p = p1 = p2.
Na compressão isobárica, diminuem
o volume (ΔV<0) e a temperatura
(ΔT<0); concluimos que o calor
cedido (Q) pelo sistema é menor
(algebricamente) que o trabalho (τ)
realizado sobre o sistema.

30. Transformação Isobárica:
A quantidade de calor trocada pelo gás, ao sofrer a variação de temperatura
ΔT numa transformação isobárica, é dada por:
Onde:
- cp é o calor específico à pressão constante
- ΔT é a variação de temperatura (K)
- m é a massa de gás
- Q é a quantidade de calor trocada

31. Aplicação:
O gráfico representa uma compressão isobárica de uma massa de 200 g de
um gás sob pressão de 2.105 N/m².
Sendo cp = 1,25 cal/(g.K) o calor
específico do hélio sob pressão constante
e 1 cal = 4,2 J, determine:
a) a quantidade de calor, em joule, que o
gás recebe durante o processo;
b) o trabalho realizado pelo gás nessa
dilatação;
c) a variação de energia interna do gás.

32. Transformação Isométrica:
O sistema não realiza nem recebe
trabalho e, portanto, a variação da
energia interna do sistema é igual à
quantidade de calor trocada por ele
com o meio externo:
ΔU = Q

33. Transformação Isométrica:
A quantidade de calor trocada pelo
gás, ao sofrer a variação de
temperatura ΔT numa transformação
isobárica, é dada por:
Onde:
- cV é o calor específico à volume constante
- ΔT é a variação de temperatura (K)
- m é a massa de gás
- Q é a quantidade de calor trocada

34. Aplicação:
Em uma transformação a volume constante, 200 g de gás ideal sofrem uma
variação de temperatura de 200 K para 600 K. Considerando o calor especí-
fico do gás a volume constante cv = 1,25 cal/g.K e 1 cal = 4,2 J, determine:
a) a quantidade de calor trocada pelo gás na transformação;
b) o trabalho realizado no processo;
c) a variação da energia interna sofrida pelo gás.

35. Transformação Adiabática:
Não há troca de calor entre o sistema e
o meio externo. Desta forma, toda
energia recebida ou cedida pelo
sistema ocorre por meio de trabalho.
Observe que:
- De 1 para 2: o gás realizou
trabalho às custas de sua
própria energia interna:
- De 2 para 3: o sistema recebe
trabalho do meio externo,
havendo uma elevação da
energia interna do gás:
−ΔU = τ
τ = ΔU

36. Transformação Adiabática:
Não há troca de calor entre o sistema e
o meio externo. Desta forma, toda
energia recebida ou cedida pelo
sistema ocorre por meio de trabalho.
Observe que:
- De 1 para 2: o gás realizou
trabalho às custas de sua
própria energia interna:
−ΔU = τ

37. Transformação Adiabática:
Não há troca de calor entre o sistema e
o meio externo. Desta forma, toda
energia recebida ou cedida pelo
sistema ocorre por meio de trabalho.
Observe que:
- De 2 para 3: o sistema recebe
trabalho do meio externo,
havendo uma elevação da
energia interna do gás:
τ = ΔU

38. Transformação Adiabática:
Não há troca de calor entre o sistema e
o meio externo. Desta forma, toda
energia recebida ou cedida pelo
sistema ocorre por meio de trabalho.
Graficamente, temos:

39. Transformação Adiabática:
R.56- Um gás perfeito sofre um processo adiabático no qual realiza um
trabalho de 300 J.
a) O gás está se expandindo ou comprimindo? Por que?
b) Qual é a quantidade de calor que o gás está trocando com o ambiente?
c) De quanto é a variação de energia interna do gás nesse processo?
d) Explique como se modificam as variáveis de estado (volume, temperatura
e pressão) do gás nessa transformação.

40. Transformação Adiabática:
R.58- Certa quantidade de gás ideal pode
passar de um estado A para um estado B por
dois “caminhos” possíveis:
transformação isocórica seguida de uma
isobárica;
transformação isobárica seguida de uma
isocórica.
Responda:
a) A que estado, A ou B, corresponde maior temperatura?
b) Qual é a variação de energia interna do gás no “caminho” 1 e no “caminho” 2?
c) Em qual dos “caminhos” é maior o trabalho realizado pelo gás? Calcule esses
trabalhos.
d) Em qual dos “caminhos” é maior a quantidade de calor trocada pelo gás?
Calcule essas quantidades de calor.

41. Transformação Cíclica:
É aquela em que certa massa de gás
ideal sofre uma série de
transformações após as quais volta ao
estado inicial de pressão, volume e
temperatura.
• Em um ciclo, o estado final é igual
ao estado inicial e, portanto, é nula
a variação da energia interna:
• Na transformação cíclica há
equivalência entre o calor total
trocado Q e o trabalho total
realizado τ.
ΔU = 0
τ = Q

42. Transformação Cíclica:
Ciclo em sentido horário: ocorre
conversão de calor em trabalho
Ciclo em sentido anti-horário: ocorre
conversão de trabalho em calor

43. Transformação Cíclica:
Chamamos de transformação útil aquela
na qual o gás absorve calor e executa
trabalho sobre o exterior: grosso modo,
uma máquina a vapor trabalha segundo
um ciclo em sentido horário, pois o calor
fornecido ao vapor transforma-se em
trabalho.
• De modo geral, dispositivos que
transformam calor em trabalho
recebem o nome de máquinas
térmicas.

44. Transformação Cíclica:
R.60 O gráfico representa a transformação cíclica sofrida por um gás ideal no
sentido ABCDA.
Pergunta-se:
a) Há conversão de calor em
trabalho ou de trabalho em
calor? Por quê?
b) Qual é a quantidade de calor
trocada no ciclo em questão? E o
trabalho realizado?

46. São aquelas que podem ocorrer em
ambos os sentidos, passando por todas
as etapas intermediárias, sem que isso
cause modificações definitivas ao meio
externo.
Transformações reversíveis:
Levando em conta as perdas de
energia por atrito e pela resistência
do ar, para fazer o bloco retornar à
posição primitiva, seria necessário
um fornecimento exterior de
energia. Nesse caso, a descida seria
irreversível.

47. Considere um bloco de massa m no
alto de um plano inclinado e, na
base do plano, uma mola
considerada ideal. Se deslizar sem
nenhuma resistência plano abaixo, o
bloco irá se chocar elasticamente
com a mola e voltará a subir pelo
plano até alcançar novamente sua
posição inicial.
São aquelas em que um sistema,
uma vez atingido o estado final de
equilíbrio, não retorna ao estado
inicial ou a quaisquer estados
intermediários sem a ação de
agentes externos.
Transformações irreversíveis:

48. Estabelece as condições nas quais é
possível a transformação de calor em
trabalho.
• Completa o primeiro princípio, que
trata apenas do balanço energético
e a equivalência entre calor e
trabalho.
O calor flui espontaneamente da
fonte mais quente para a fonte
fria. No entanto, a passagem
contrária não ocorre.
O calor passa espontaneamente do corpo de maior temperatura para o
corpo de menor temperatura.

49. Uma gota de tinta coloca num líquido
espalha-se uniformemente por ele, de
modo espontâneo
Porém, praticamente inexiste a
possibilidade das moléculas de tinta
se reagruparem para formar a gota
de tinta inicial!!!!

50. É impossível construir uma máquina
térmica, operando em ciclos, cujo
único efeito seja retirar calor de uma
fonte e convertê-lo integralmente em
trabalho.
Máquinas térmicas – Conversão de calor em trabalho
Para que uma máquina térmica converta
calor em trabalho de modo contínuo,
deve operar em ciclo entre duas fontes
térmicas, uma quente e outra fria:
- retira calor da fonte quente (Q1)
- converte-o parcialmente em trabalho
- transfere o restante (Q2) para a fonte
fria

51. É impossível construir uma máquina
térmica, operando em ciclos, cujo
único efeito seja retirar calor de uma
fonte e convertê-lo integralmente em
trabalho.
Máquinas térmicas – Conversão de calor em trabalho
𝜏 = 𝑄1 − 𝑄2
• Q1 é a quantidade total de calor
retirada da fonte quente.
• Q2 é a quantidade de calor
dissipada para a fonte fria.

52. Máquinas térmicas – Conversão de calor em trabalho
O rendimento (η) de uma máquina
térmica é expresso pela razão entre a
quantidade útil (trabalho) e a
quantidade total de energia (fonte
quente).
𝜂 =
𝜏
𝑄1
𝜂 =
𝐸𝑛𝑒𝑟𝑔𝑖𝑎 ú𝑡𝑖𝑙
𝐸𝑛𝑒𝑟𝑔𝑖𝑎 𝑡𝑜𝑡𝑎𝑙
Como τ = Q1 – Q2, temos que:
𝜂 = 1 −
𝑄2
𝑄1
ATENÇÃO!! O rendimento de uma máquina térmica é
expresso em porcentagem (%).

53. R.61 Uma caldeira, à temperatura de 600 K (fonte quente), fornece vapor
correspondente a 1.000 kcal em cada segundo a uma turbina. O vapor, depois
de passar pela turbina, cede ao condensador (fonte fria) 800 kcal por
segundo a uma temperatura de 293 K. Considerando 1 cal = 4 J, determine a
potência produzida por essa máquina em kW e calcule seu rendimento.

54. Máquinas frigoríficas são dispositivos
que convertem trabalho em calor.
Refrigerador – Conversão de trabalho em calor
A eficiência (e) de uma máquina
frigorífica é expressa pela quantidade
de calor retirada da fonte fria (Q2) e o
trabalho externo envolvido na
transferência (τ).
𝑒 =
𝑄2
𝜏

55. R.62 Numa máquina frigorífica, em cada ciclo do gás utilizado, são retirados
120 J do congelador. No processo a atmosfera (fonte quente) recebe 150 J.
Determine:
a) o trabalho do compressor em cada ciclo;
b) a eficiência dessa máquina térmica.

56. Estabelece as condições em que uma
máquina térmica realiza um ciclo de
rendimento teórico máximo.
Ciclo de Carnot
O rendimento no ciclo de Carnot é
função exclusiva das temperaturas
absolutas das fontes quente (T1) e
fria (T2), não dependendo,
portanto, da substância
“trabalhante” utilizada.

57. Estabelece as condições em que uma
máquina térmica realiza um ciclo de
rendimento teórico máximo.
Ciclo de Carnot O teorema de Carnot divide-se em
duas partes:
• A máquina de Carnot tem
rendimento maior que qualquer
outro tipo de máquina,
operando com as mesmas
fontes.
• Todas as máquinas de Carnot
têm o mesmo rendimento,
desde que operem entre as
mesmas fontes.
𝜂 = 1 −
𝑇2
𝑇1
Máximo rendimento de
uma máquina térmica

58. Ciclo de Carnot
R.63 Certa máquina térmica ideal funciona realizando o ciclo de Carnot. Em
cada ciclo, o trabalho útil fornecido pela máquina é de 1.000 J. Sendo as
temperaturas das fontes térmicas 127 °C e 27 °C, respectivamente,
determine:
a) o rendimento dessa máquina;
b) a quantidade de calor retirada da fonte quente;
c) a quantidade de calor rejeitada para a fonte fria.