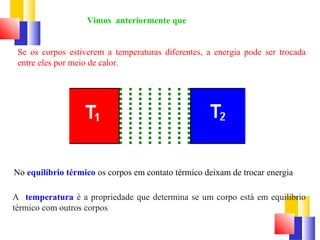
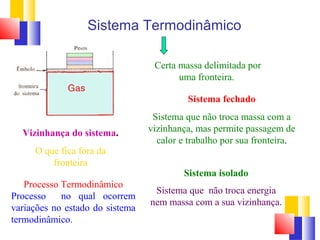
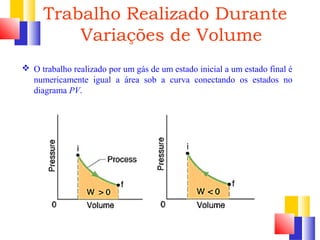
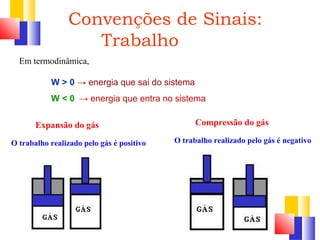
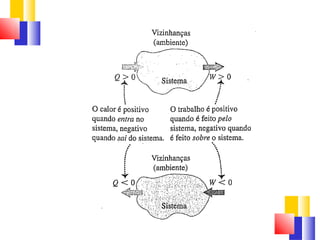
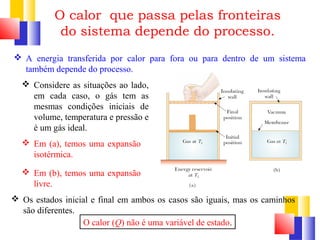
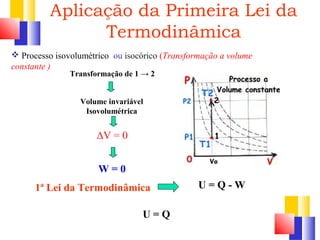
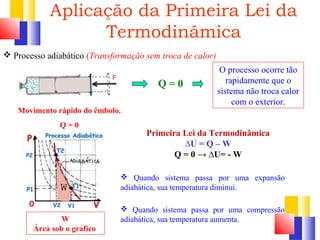
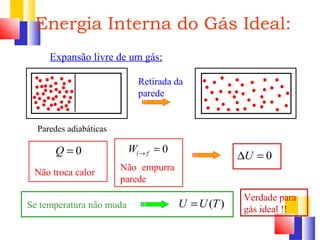
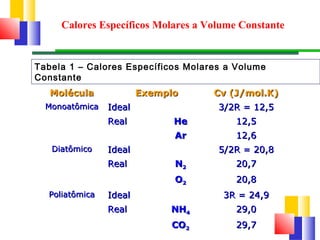
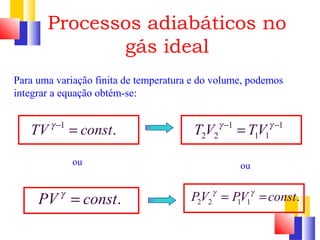
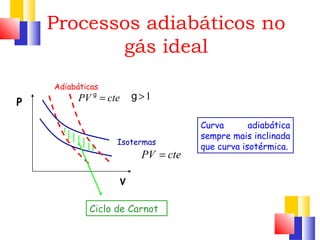
O documento discute a Primeira Lei da Termodinâmica, explicando que ela é uma generalização da lei da conservação de energia que inclui mudanças na energia interna de um sistema. A Primeira Lei estabelece que a variação na energia interna de um sistema é igual à quantidade de calor adicionado menos o trabalho realizado. Exemplos ilustram como aplicar a lei a diferentes processos termodinâmicos.

1. Universidade Federal Rural
do Semi-Árido - UFERSA
Primeira Lei da Termodinâmica
Jusciane da Costa e Silva
Mossoró, Junho de 2010

2. Sumário
 Introdução
 Trabalho e Calor Em Processos Termodinâmicos
 Mecanismo de Transferência de Energia em Processos
Termodinâmicos
 Primeira Lei da Termodinâmica e Energia Interna
 Aplicações da Primeira Lei da Termodinâmica

3. Vimos anteriormente que
Se os corpos estiverem a temperaturas diferentes, a energia pode ser trocada
entre eles por meio de calor.
No equilíbrio térmico os corpos em contato térmico deixam de trocar energia
A temperatura é a propriedade que determina se um corpo está em equilíbrio
térmico com outros corpos

4. Sistema Termodinâmico
Certa massa delimitada por
uma fronteira.
Vizinhança do sistema.
O que fica fora da
fronteira
Sistema fechado
Sistema que não troca massa com a
vizinhança, mas permite passagem de
calor e trabalho por sua fronteira.
Sistema isolado
Sistema que não troca energia
nem massa com a sua vizinhança.
Processo Termodinâmico
Processo no qual ocorrem
variações no estado do sistema
termodinâmico.

5. Calor e Primeira Lei da
Termodinâmica
 Até por volta de 1850, os campos da termodinâmica e da mecânica eram
considerados dois ramos distintos.
 A lei da conservação da energia parecia descrever somente certos tipos de
sistemas mecânicos.
 James Joule e outros cientistas mostraram que a energia pode ser
adicionada (ou removida) de um sistema, ou por calor, ou realizando
trabalho sobre ele.
 O conceito de energia foi ampliado para incluir a energia interna e essa
expansão da conservação da energia é chamada de primeira lei da
termodinâmica.
 A lei da conservação da energia emerge como uma lei universal da
natureza.

6. Trabalho Realizado Durante
Variações de Volume
 O trabalho realizado pelo gás sobre o
pistão:
dW = Fdy = PAdy
ou
dW = PdV
O trabalho total realizado pelo gás à medida
que o seu volume se altera de Vi para Vf é
dado por
V
V
= ò f
W PdV
i

7. Trabalho Realizado Durante
Variações de Volume
 O trabalho realizado por um gás de um estado inicial a um estado final é
numericamente igual a área sob a curva conectando os estados no
diagrama PV.

8. Convenções de Sinais:
Trabalho
Em termodinâmica,
W > 0 → energia que sai do sistema
W < 0 → energia que entra no sistema
Expansão do gás Compressão do gás
O trabalho realizado pelo gás é positivo O trabalho realizado pelo gás é negativo

9. Convenções de Sinais:
Calor
Calor - Modo de transferência de energia resultante da diferença de
temperatura entre dois sistemas (ou um sistema e a vizinhança):
Q > 0 → calor que entra no sistema
Q < 0 → calor que sai do sistema

11. Exemplo 1
Expansão isotérmica de um gás ideal – Um gás sofre uma expansão isotérmica
(a temperatura constante) para uma temperatura T, enquanto o volume varia
entre os limites V1 e V2. Qual o trabalho realizado pelo gás?
V
V
W PdV
P = nRT
V
= ò f
i
De acordo com a equação do gás ideal: PV=nRT, assim
Assim a equação do trabalho torna-se:
nRT V
ln 2
V
1
W nRT dV f
= ò =
V
V
V
i
Além disso T é constante:
V = P
1
Logo,
2
2
1
P
V
W = nRT P
ln 1
P
2

12. O trabalho realizado pelo sistema
depende do processo.
 O trabalho realizado por um sistema depende dos estados inicial e final e
do caminho seguido pelo sistema entre estes estados:
( ) W PdV i f i ( ) W =P V -V f f i W =P V -V
O trabalho (W) não é uma variável de estado.
V
V
= ò f
i

13. O calor que passa pelas fronteiras
do sistema depende do processo.
 A energia transferida por calor para fora ou para dentro de um sistema
também depende do processo.
 Considere as situações ao lado,
em cada caso, o gás tem as
mesmas condições iniciais de
volume, temperatura e pressão e
é um gás ideal.
 Em (a), temos uma expansão
isotérmica.
 Em (b), temos uma expansão
livre.
 Os estados inicial e final em ambos os casos são iguais, mas os caminhos
são diferentes.
O calor (Q) não é uma variável de estado.

14. Primeira Lei da Termodinâmica
 A primeira lei da termodinâmica é uma generalização da lei da
conservação da energia que engloba mudanças na energia interna.
Energia interna é toda a energia de um sistema que está associada com suas
componentes microscópicas – átomos e moléculas – quando vistas de um
sistema de referência em repouso com respeito ao objeto.
 Energia interna:
- Energia cinética de translação, de rotação ou de vibração das moléculas;
- Energia potencial das moléculas;
- Energia potencial entre moléculas.
 Há dois mecanismos pelos quais podemos alterar a energia interna do
sistema:
- Processos envolvendo a transferência de energia pela realização de
trabalho;
- Processos envolvendo a transferência de energia pela troca de calor.

15. Primeira Lei da Termodinâmica
 Portanto, podemos definir a primeira lei da termodinâmica como:
DU = Q -W
Conservação
de energia
Q > 0 ® calor adicionado ao sistema (U aumenta)
Q < 0 ® calor retirado do sistema (U diminui)
W > 0 ® trabalho realizado pelo sistema (U diminui)
W < 0 ® trabalho realizado sobre o sistema (U aumenta)
 Embora Q e W dependam do caminho escolhido, a quantidade Q – W é
independente do caminho.
A energia interna (Eint) é uma variável de estado.

16. Por Exemplo,
A Energia interna de uma xícara de café depende apenas do seu estado
termodinâmico – quais são as quantidades de água e de pó de café existente
no sistema, e qual é a sua temperatura. Ela não depende da história do modo
como ele foi preparado, ou seja, do caminho termodinâmico que conduziu o
sistema o sistema até o estado em que ele se encontra

17. Exemplo 2
Deve-se converter 1 kg de água a 100 0 C em vapor d´água na mesma temperatura
à pressão atmosférica (P = 1,01.105 N/m2). O volume da água varia de 1,0 x10-6
m3 do líquido para 1671x10-6 m3 de gás. O calor de vaporização para essa pressão
é Lv = 2.256 x 106 J/kg.
a) Qual o trabalho realizado pelo sistema?
b) Qual a variação da energia interna do sistema?
DU = Q -W Sendo,
DU = Q -W = 2256kJ -169kJ = 2290kJ
( )
KJ
Kg Kg
Q mL kJ v
2256
2256 1,00
=
÷ø ö
çè æ
= =

18. Quando um sistema é levado do estado i para o estado f ao longo da trajetória iaf
na figura à seguir, Q = 50cal e W = 20cal . Ao longo da trajetória ibf , Q = 36cal .
a) Qual o valor do trabalho ao longo da trajetória ibf?
U Q W cal if iaf iaf D = - = 30
Mas por outro lado,
Exemplo 3
U Q W W Q U cal ibf ibf ibf ibf D = - ® = - D = 6
b) Se W = -13cal para a trajetória de volta fi , qual será Q para essa trajetória?
if f i fi i f DU =U -U ®DU =U -U
Assim,
U U cal fi if D = -D = -30
Logo,
Q U W cal fi fi fi = D + = -43

19. Aplicação da Primeira Lei da
Termodinâmica
 Processo isovolumétrico ou isocórico (Transformação a volume
constante )
Transformação de 1 → 2
Volume invariável
Isovolumétrica
ΔV = 0
W = 0
1ª Lei da Termodinâmica
U = Q - W
U = Q

20. Aplicação da Primeira Lei da
 Processo Isotérmico (Transformação a temperatura constante )
Êmbolo movimentado
lentamente
1ª Lei da Termodinâmica
U = 0 → ΔT=0
Q = W
Termodinâmica

21. Aplicação da Primeira Lei da
Termodinâmica
 Processo adiabático (Transformação sem troca de calor)
Movimento rápido do êmbolo.
Q = 0
Q = 0
O processo ocorre tão
rapidamente que o
sistema não troca calor
com o exterior.
Primeira Lei da Termodinâmica
ΔU = Q – W
Q = 0 → ΔU= - W
W
Área sob o grafico
 Quando sistema passa por uma expansão
adiabática, sua temperatura diminui.
 Quando sistema passa por uma compressão
adiabática, sua temperatura aumenta.

22. Aplicação da Primeira Lei da
Termodinâmica
 Processo Cíclicos (Estado inicial é igual ao Estado Final )
1.- ΔUciclo = SΔU = 0
2.- Qciclo = SQ
3.- Wciclo = SW = área 12341
1a Lei da Termodinâmica
ΔUciclo = Qciclo - Wciclo
Qciclo = Wciclo
Wciclo > 0 → Qciclo > 0
O sentido do ciclo no diagrama P´V : horário.
O sistema recebe Q e entrega W

23. Aplicação da Primeira Lei da
Termodinâmica
• Expansão livre : São processos adiabáticos nos quais nenhum trabalho é
realizado.
Q =W +U
Q =W = 0
U = 0
A temperatura do gás no estado inicial e final tem que ser a mesma.
São processos súbitos em que não se conhece a pressão e volume nos
estados intermediários.

24. Primeira Lei da Termodinâmica
Resumo

25. Energia Interna do Gás Ideal:
Expansão livre de um gás:
Retirada da
parede
Paredes adiabáticas
0 i f W® =
Q = 0 DU = 0
Não troca calor
Não empurra
parede
Se temperatura não muda U =U(T) Verdade para
gás ideal !!

26. Calor Específico de Um
= ¢ - ¢
= -
Gás Ideal:
dU d Q d W
dU nCdT PdV
V cte
P cte
Primeira lei:
a V V dU = d¢Q = nC dT
b P P dU = d¢Q - d¢W = nC dT - PdV
a b Gás Ideal: U depende apenas da dU = dU
temperatura
Então: P V C = C + R Concorda para gases
monoatômicos e diatômicos

27. Calores Específicos Molares a Volume Constante
Tabela 1 – Calores Específicos Molares a Volume
Constante
MMoollééccuullaa EExxeemmpplloo CCvv ((JJ//mmooll..KK))
MMoonnooaattôômmiiccaa IIddeeaall 33//22RR == 1122,,55
RReeaall HHee 1122,,55
AArr 1122,,66
DDiiaattôômmiiccoo IIddeeaall 55//22RR == 2200,,88
RReeaall NN22 2200,,77
OO22 2200,,88
PPoolliiaattôômmiiccaa IIddeeaall 33RR == 2244,,99
RReeaall NNHH44 2299,,00
CCOO22 2299,,77

28. Processos adiabáticos no
gás ideal
Definições: Pela primeira lei da termodinâmica, temos:
¢ =
= - ¢
d Q 0
dU d W
V dU = nC dT
Para um gás ideal em qualquer
processo com variação dT.
Usando a equação de estado do gás ideal nas relações acima podemos
escrever
C
C
onde P
V
g =
dT + ( g - 1) dV =
0
T V

29. Processos adiabáticos no
gás ideal
Para uma variação finita de temperatura e do volume, podemos
integrar a equação obtém-se:
TVg -1 = const.
ou
2 2 1 1 T V g - = TVg -
1 1
ou
2 2 1 1 PVg = const. PV g = PVg =const.

30. Processos adiabáticos no
gás ideal
Curva adiabática
sempre mais inclinada
que curva isotérmica.
Adiabáticas
PV g = cte
g >1
PV = cte
V
P
Isotermas
Ciclo de Carnot

31. Processos adiabáticos no
Trabalho realizado num processo adiabático
P
W = nc T - T ® W = c PV -
PV
V
Vi Vf
dU = -W ®ncvdT = -W
W = PV -
PV
1 1 2 2
1 2
( )
1
® g
-
gás ideal
1 2 1 1 1 1 ( ) v ( )
v
R

32. Bibliografia
 H. Moysés Nussenzveig, Curso de Física Básico, Vol. 2.
 D. Halliday, R. Resnick, J. Walker, Fundamentos de Física,
Vol. 2.