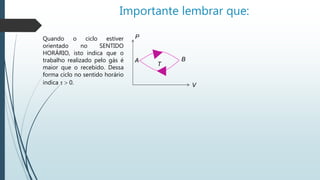
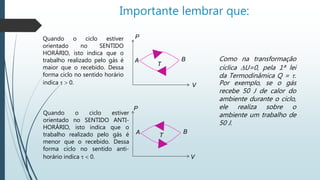
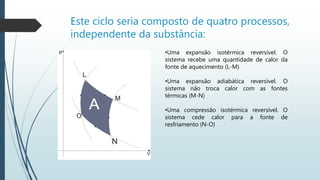
Uma transformação cíclica de um gás envolve uma sequência de transformações que retorna o gás ao seu estado inicial de pressão, temperatura e volume. O documento descreve um ciclo ABCDA de um gás, incluindo as etapas de expansão e compressão isobárica e transformações isocóricas, além de explicar a relação entre trabalho e calor em um processo cíclico.

1. Transformações Cíclicas

2. Transformações Cíclicas
transformação cíclica de uma massa gasosa é uma sequência de transformações
gasosas em que, ao final de cada transformação, o gás retorna ao seu estado inicial de
Pressão, Temperatura e Volume. Portanto, o estado final coincide com o estado inicial.

3. Observe o gráfico a seguir:
Expansão isobárica AB e
Transformação isocórica BC

4. Observe o gráfico a seguir:
Expansão isobárica AB e
Transformação isocórica BC
Sendo um gás qualquer, sofrendo uma transformação A – C, onde o gás realiza uma
expansão isobárica AB, seguida de uma diminuição isocórica BC.
O trabalho realizado na transformação A – C é dado pelo cálculo da área da figura
formada abaixo do gráfico, sendo ele maior do que zero (W1 > 0).

5. Considere agora que o gás volte ao seu estado inicial, realizando a transformação C
– A, onde realiza uma compressão isobárica CD, seguida de um aumento isocórico
DA, como mostra o gráfico abaixo:
Compressão isobárica CD
Transformação isocórica DA

6. Considere agora que o gás volte ao seu estado inicial, realizando a transformação C
– A, onde realiza uma compressão isobárica CD, seguida de um aumento isocórico
DA, como mostra o gráfico abaixo:
Compressão isobárica CD
Transformação isocórica DA
Podemos observar que, como o gás sofre uma compressão isobárica, ou seja, houve
uma diminuição do volume à pressão constante, o trabalho realizado é menor do
que zero (W2 < 0).

7. Ao final do processo, o gás completa um ciclo ABCDA, onde o trabalho total
realizado é a soma algébrica dos trabalhos realizados nas diferentes etapas do
ciclo.
W = W1 + W2
Ciclo ABCDA, a área sombreada
é numericamente igual ao trabalho
realizado.

8. Ao final do processo, o gás completa um ciclo ABCDA, onde o trabalho total
realizado é a soma algébrica dos trabalhos realizados nas diferentes etapas do
ciclo.
W = W1 + W2
Ciclo ABCDA, a área sombreada
é numericamente igual ao trabalho
realizado.
O trabalho total (W) é positivo, pois |W1| > |W2|, sendo calculado
numericamente pela área da figura formada pelo ciclo.

9. A quantidade de calor total trocada em todo o ciclo também é dada pela soma
algébrica das quantidades de calor trocadas em cada etapa do ciclo, ou seja:
Q = QAB + QBC + QCD + QDA
Na transformação cíclica o estado final é igual ao estado inicial, implica que a
variação da energia interna é nula (∆U = 0).
Sabendo que: ∆U = Q – W W = Q
Portanto, no ciclo existe uma equivalência entre o calor trocado Q e o trabalho
realizado W.
temos que:

11. Importante lembrar que:
B
V
T
A
Quando o ciclo estiver
orientado no SENTIDO
HORÁRIO, isto indica que o
trabalho realizado pelo gás é
maior que o recebido. Dessa
forma ciclo no sentido horário
indica   0.
P

12. Importante lembrar que:
B
TA
B
V
T
A
Quando o ciclo estiver
orientado no SENTIDO
HORÁRIO, isto indica que o
trabalho realizado pelo gás é
maior que o recebido. Dessa
forma ciclo no sentido horário
indica   0.
Quando o ciclo estiver
orientado no SENTIDO ANTI-
HORÁRIO, isto indica que o
trabalho realizado pelo gás é
menor que o recebido. Dessa
forma ciclo no sentido anti-
horário indica   0. V
P
P

13. Importante lembrar que:
B
TA
B
V
T
A
Quando o ciclo estiver
orientado no SENTIDO
HORÁRIO, isto indica que o
trabalho realizado pelo gás é
maior que o recebido. Dessa
forma ciclo no sentido horário
indica   0.
Quando o ciclo estiver
orientado no SENTIDO ANTI-
HORÁRIO, isto indica que o
trabalho realizado pelo gás é
menor que o recebido. Dessa
forma ciclo no sentido anti-
horário indica   0. V
P
P
Como na transformação
cíclica U=0, pela 1ª lei
da Termodinâmica Q = .
Por exemplo, se o gás
recebe 50 J de calor do
ambiente durante o ciclo,
ele realiza sobre o
ambiente um trabalho de
50 J.

14. Exemplo 1:
 (OSEC) Quando um gás perfeito descreve um ciclo, sua energia interna:
 A) aumenta
 B) diminui.
 C) Vária, mas o valor final é igual ao valor inicial.
 D) Não pode ser determinada.
 E) Permanece constante.

15. Exemplos:
 (OSEC) Quando um gás perfeito descreve um ciclo, sua energia interna:
 A) aumenta
 B) diminui.
 C) Vária, mas o valor final é igual ao valor inicial. V
 D) Não pode ser determinada.
 E) Permanece constante.

16. Exemplo 2:
 Conforme o gráfico abaixo responda:
a) A conversão de Q W ou W Q?
b) Qual a quantidade de calor trocada no ciclo, e qual o trabalho realizado?

17. Exemplo 2:
 Conforme o gráfico abaixo responda:
a) A conversão de Q W ou W Q? R = Q W
b) Qual a quantidade de calor trocada no ciclo, e qual o trabalho realizado?
b) W > 0
W = 6.103 + 3.103 . 4 = 9.103 . 4 = 18.103 J
2 2
U = 0 U = Q – W Q = W = 18.103 J

18. Ciclo de Carnot
Até meados do século XIX, acreditava-se ser possível a construção de uma máquina
térmica ideal, que seria capaz de transformar toda a energia fornecida em trabalho,
obtendo um rendimento total (100%).
Para demonstrar que não seria possível, o engenheiro francês Nicolas Carnot (1796-
1832) propôs uma máquina térmica teórica que se comportava como uma máquina de
rendimento total, estabelecendo um ciclo de rendimento máximo, que mais tarde
passou a ser chamado Ciclo de Carnot.

19. •Uma expansão isotérmica reversível. O
sistema recebe uma quantidade de calor da
fonte de aquecimento (L-M)
Este ciclo seria composto de quatro processos,
independente da substância:

20. •Uma expansão isotérmica reversível. O
sistema recebe uma quantidade de calor da
fonte de aquecimento (L-M)
•Uma expansão adiabática reversível. O
sistema não troca calor com as fontes
térmicas (M-N)
Este ciclo seria composto de quatro processos,
independente da substância:

21. •Uma expansão isotérmica reversível. O
sistema recebe uma quantidade de calor da
fonte de aquecimento (L-M)
•Uma expansão adiabática reversível. O
sistema não troca calor com as fontes
térmicas (M-N)
•Uma compressão isotérmica reversível. O
sistema cede calor para a fonte de
resfriamento (N-O)
Este ciclo seria composto de quatro processos,
independente da substância:

22. •Uma expansão isotérmica reversível. O
sistema recebe uma quantidade de calor da
fonte de aquecimento (L-M)
•Uma expansão adiabática reversível. O
sistema não troca calor com as fontes
térmicas (M-N)
•Uma compressão isotérmica reversível. O
sistema cede calor para a fonte de
resfriamento (N-O)
•Uma compressão adiabática reversível. O
sistema não troca calor com as fontes
térmicas (O-L)
Este ciclo seria composto de quatro processos,
independente da substância:

23. Numa máquina de Carnot, a quantidade de calor que é fornecida pela fonte de aquecimento e a
quantidade cedida à fonte de resfriamento são proporcionais às suas temperaturas absolutas, assim:
Assim, o rendimento de uma máquina de Carnot é: e
Logo: Trabalho realizado: W = Q2 – Q1
Sendo:
= temperatura absoluta da fonte de resfriamento
= temperatura absoluta da fonte de aquecimento
Com isto se conclui que para que haja 100% de rendimento, todo o calor vindo da fonte de
aquecimento deverá ser transformado em trabalho, pois a temperatura absoluta da fonte de
resfriamento deverá ser 0K.
Partindo daí conclui-se que o zero absoluto não é possível para um sistema físico.

24. Exemplo:
Qual o rendimento máximo teórico de uma máquina à vapor, cujo fluido entra a 560ºC
e abandona o ciclo a 200ºC?

25. Experimento 1 – Bexiga na seringa:
1

26. Experimento 1 – Bexiga na seringa:
1
2
compressão Isotérmica

27. Experimento 1 – Bexiga na seringa:
1
23
compressão IsotérmicaExpansão Adiabática

28. O que aconteceu?
 Quando pressionado, o ar dentro da seringa fez com que o volume da
bexiga diminuísse sem nenhuma variação na massa (compressão
Isométrica). Conforme a pressão diminuiu a bexiga volta ao seu estado
normal (expansão adiabática), completando assim um ciclo.

29. Grupo:
 Cleverthon Witor Amorim do Nascimento
 Ewellen Karoline de Souza Santos
 José Bruno Bezerra da Silva
 Sebastião Inácio da Silva Neto
Prof.: Gentil Luiz
Disciplina: Física
Transformações Cíclicas e Ciclo de Carnot