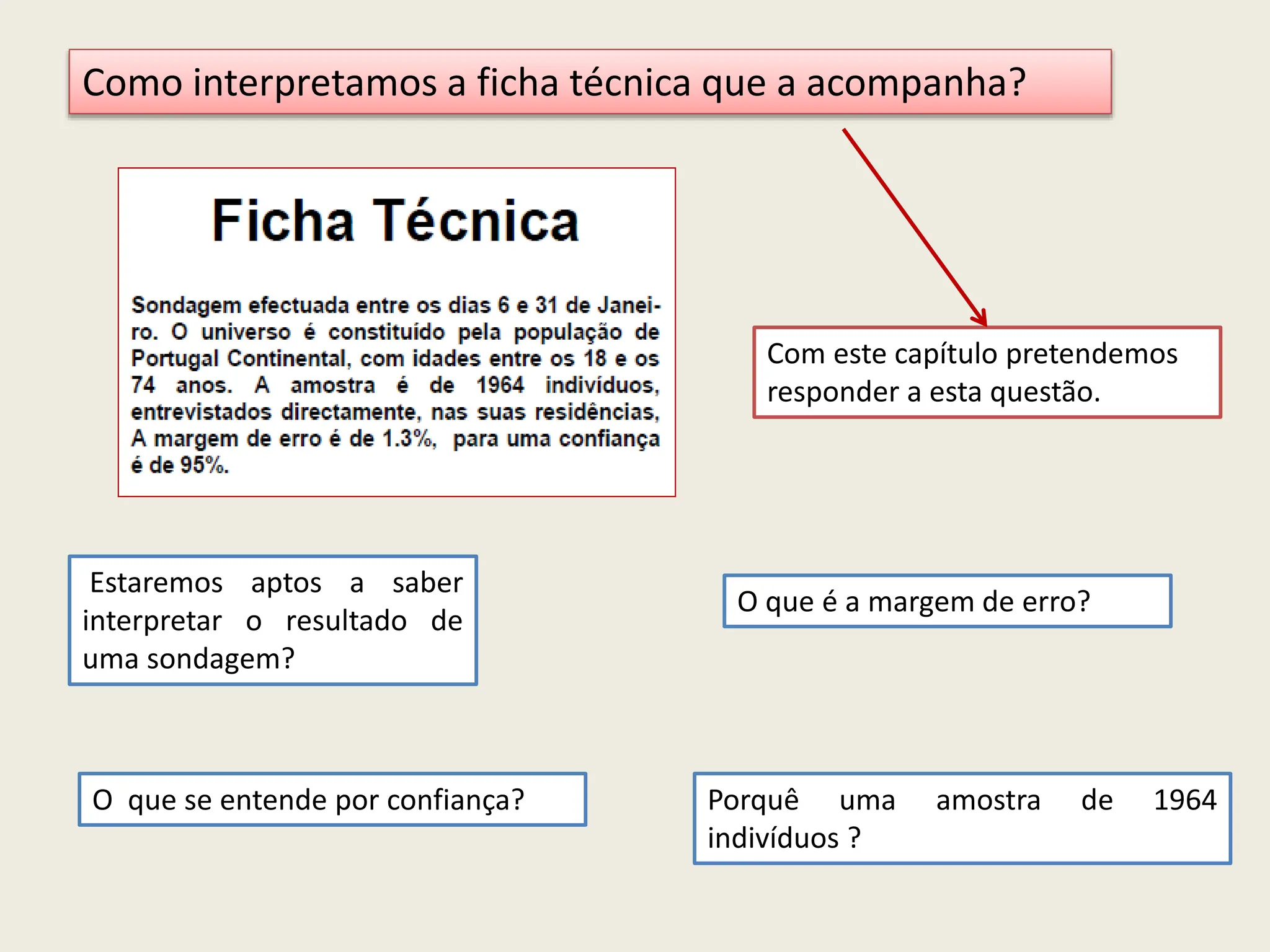
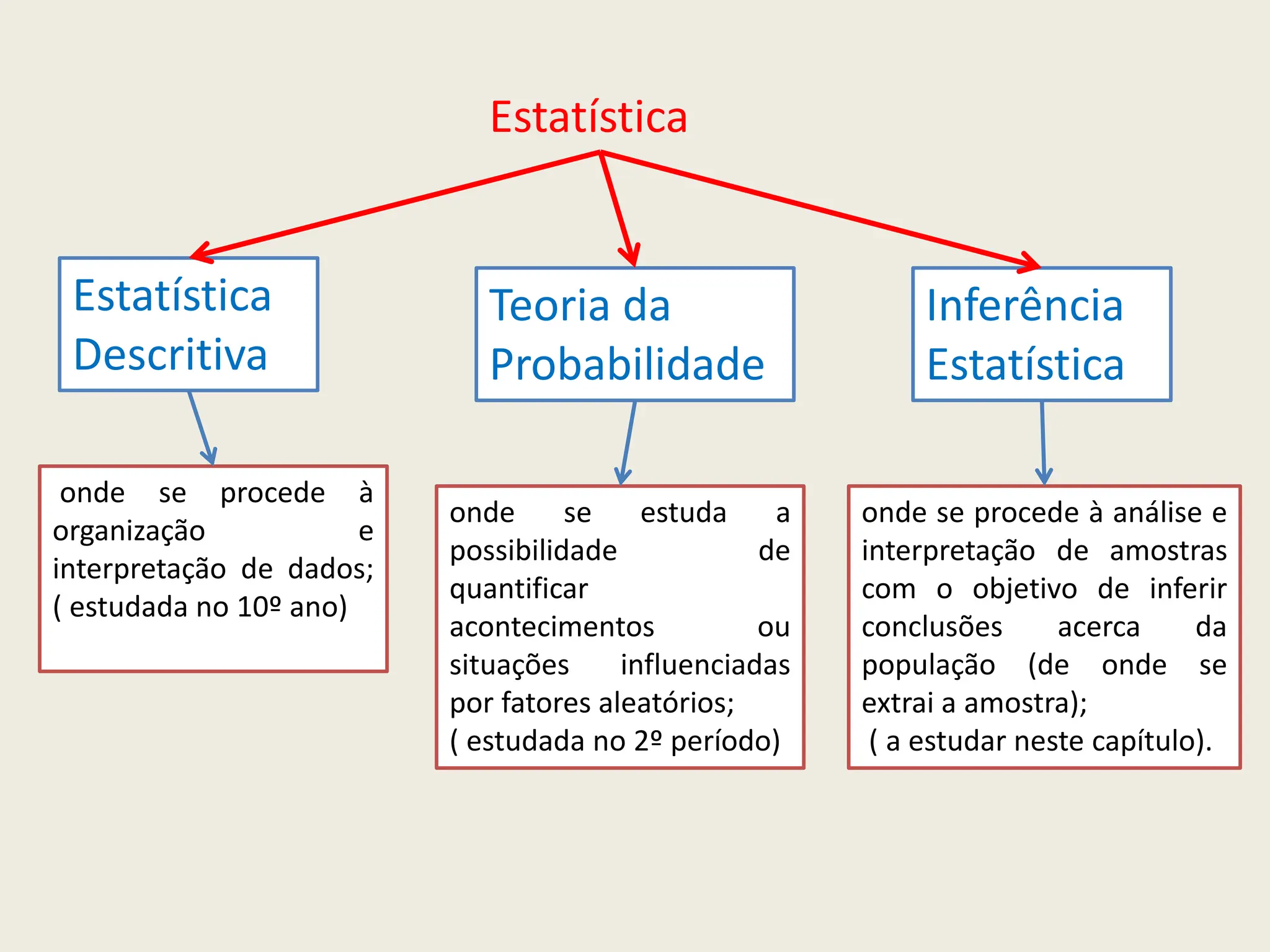
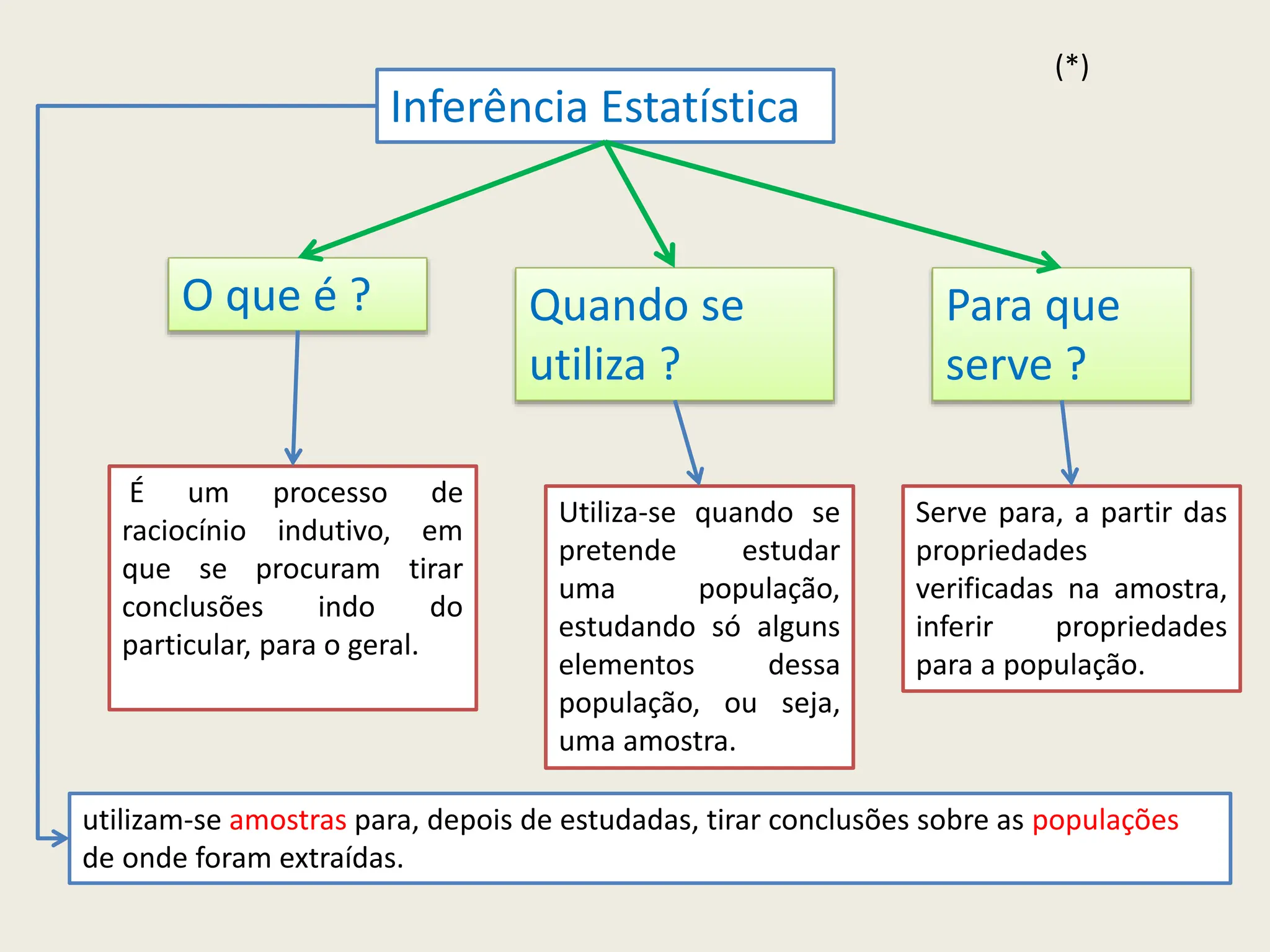
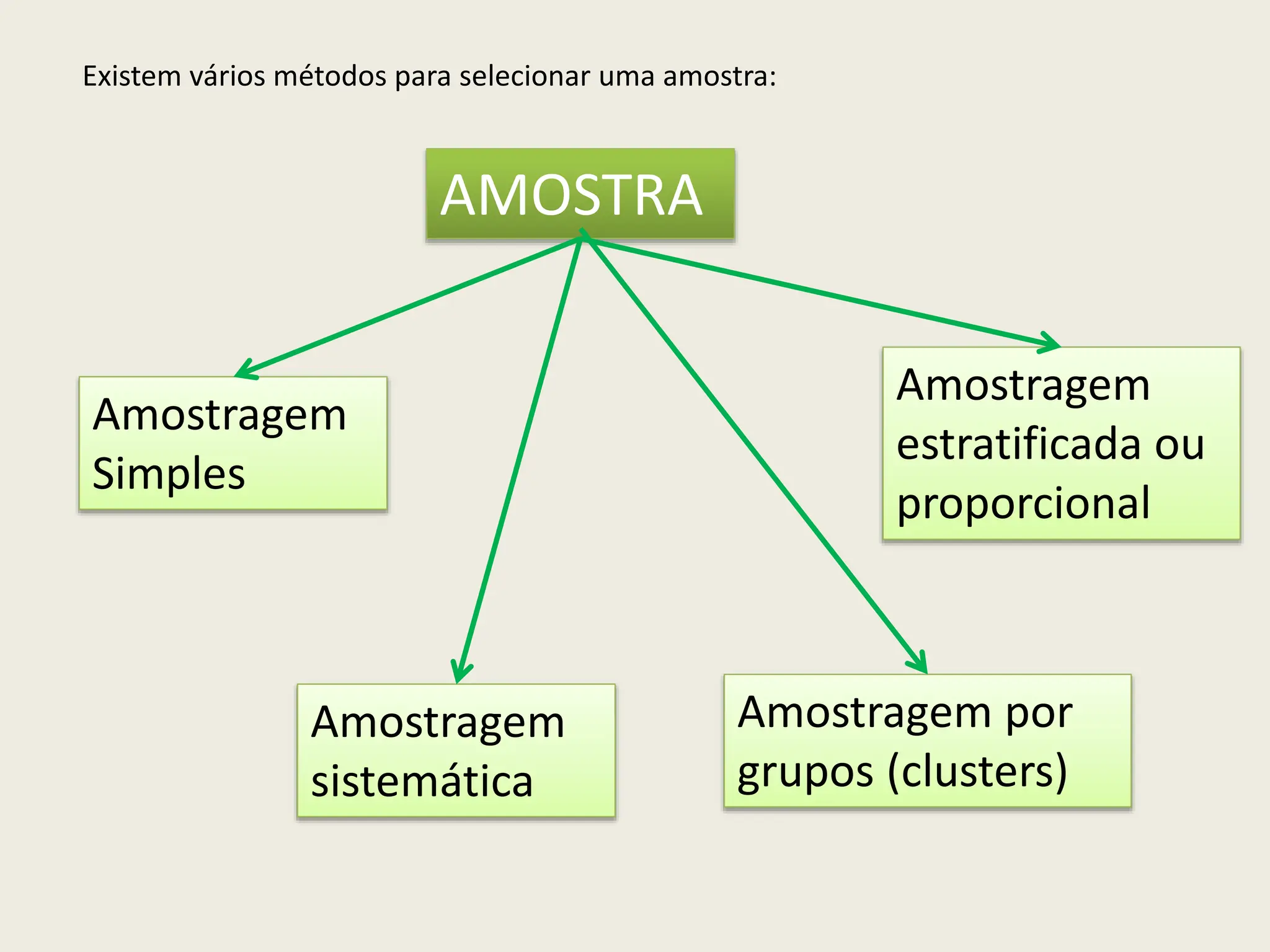
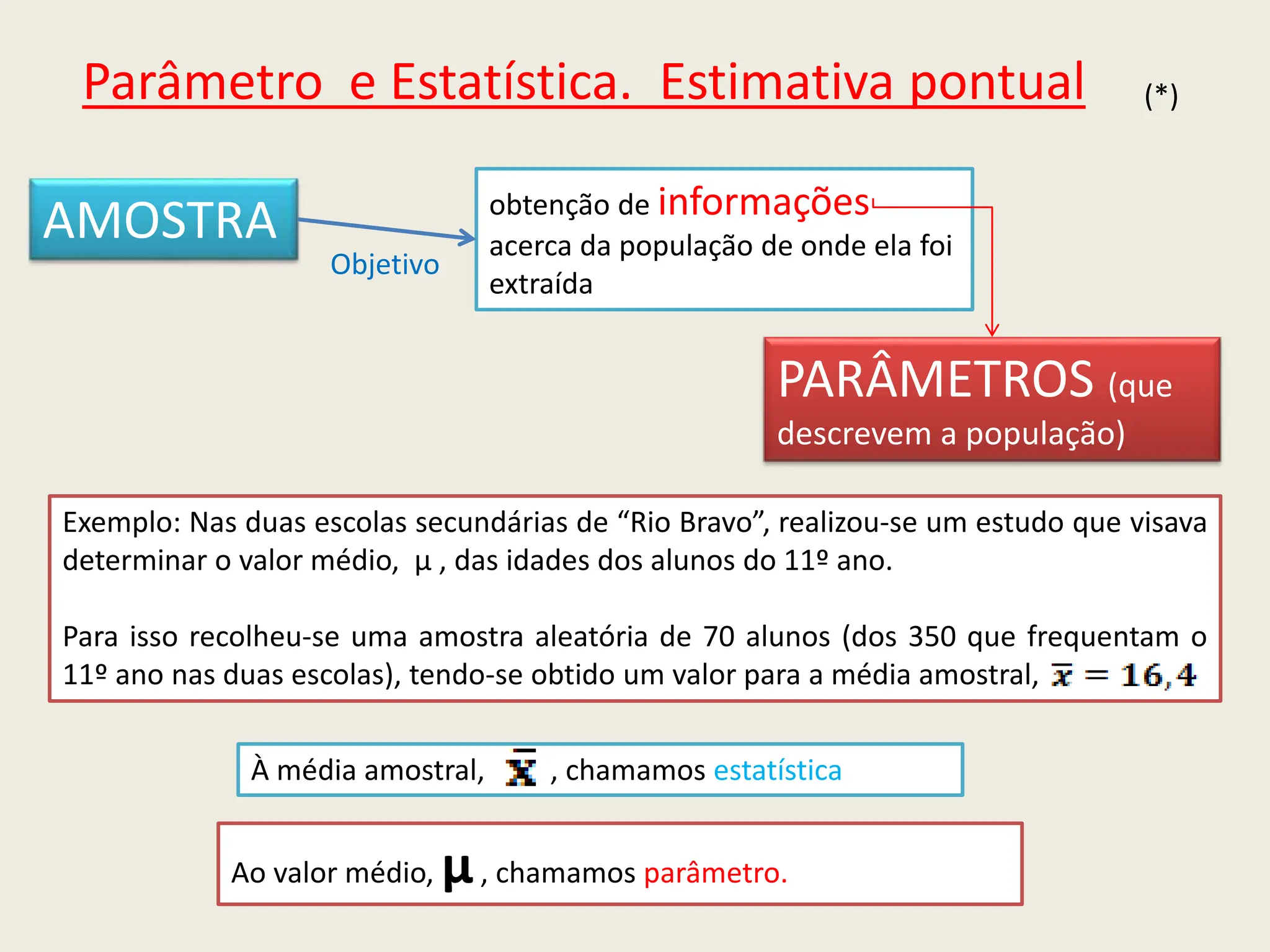
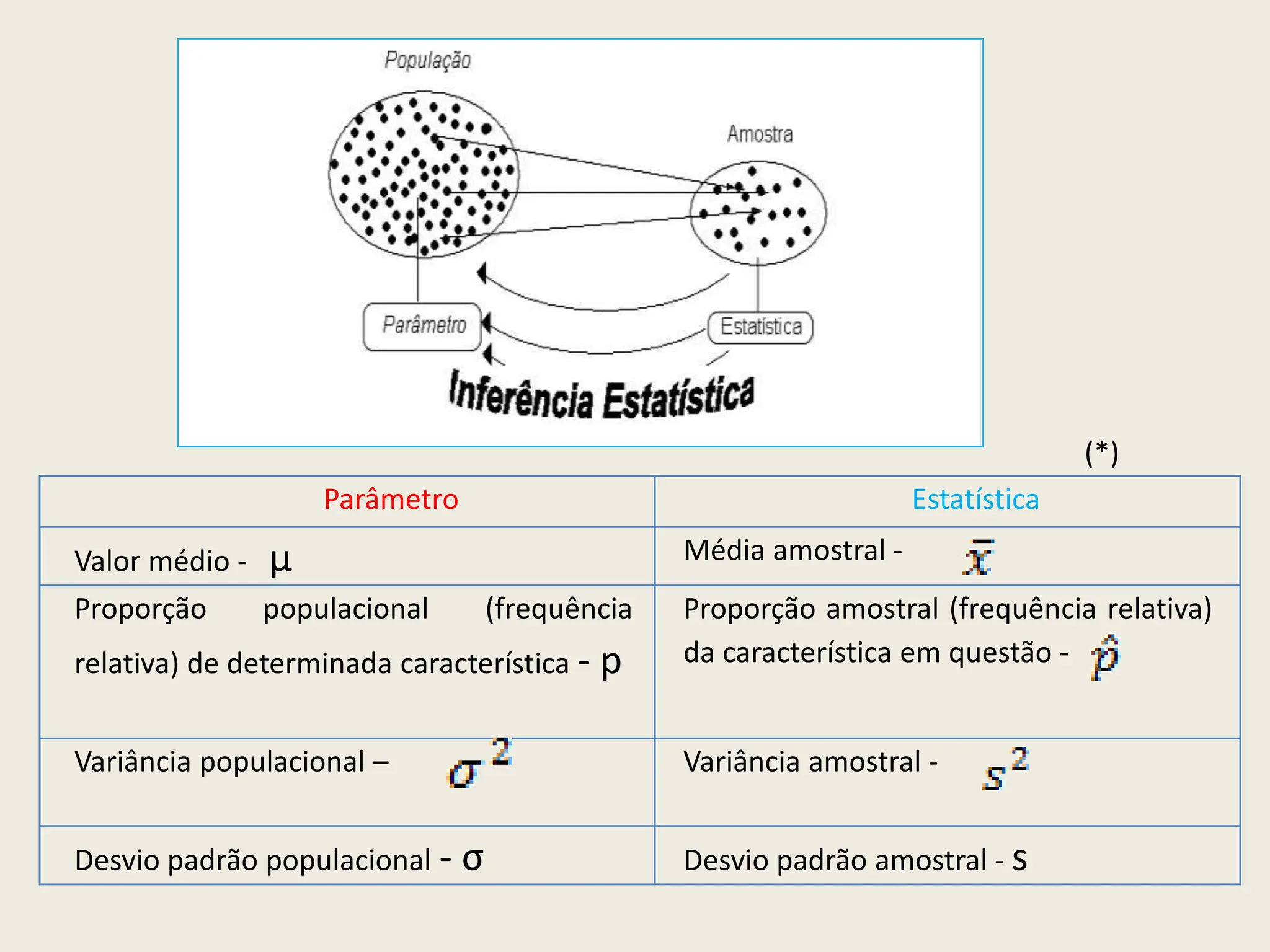
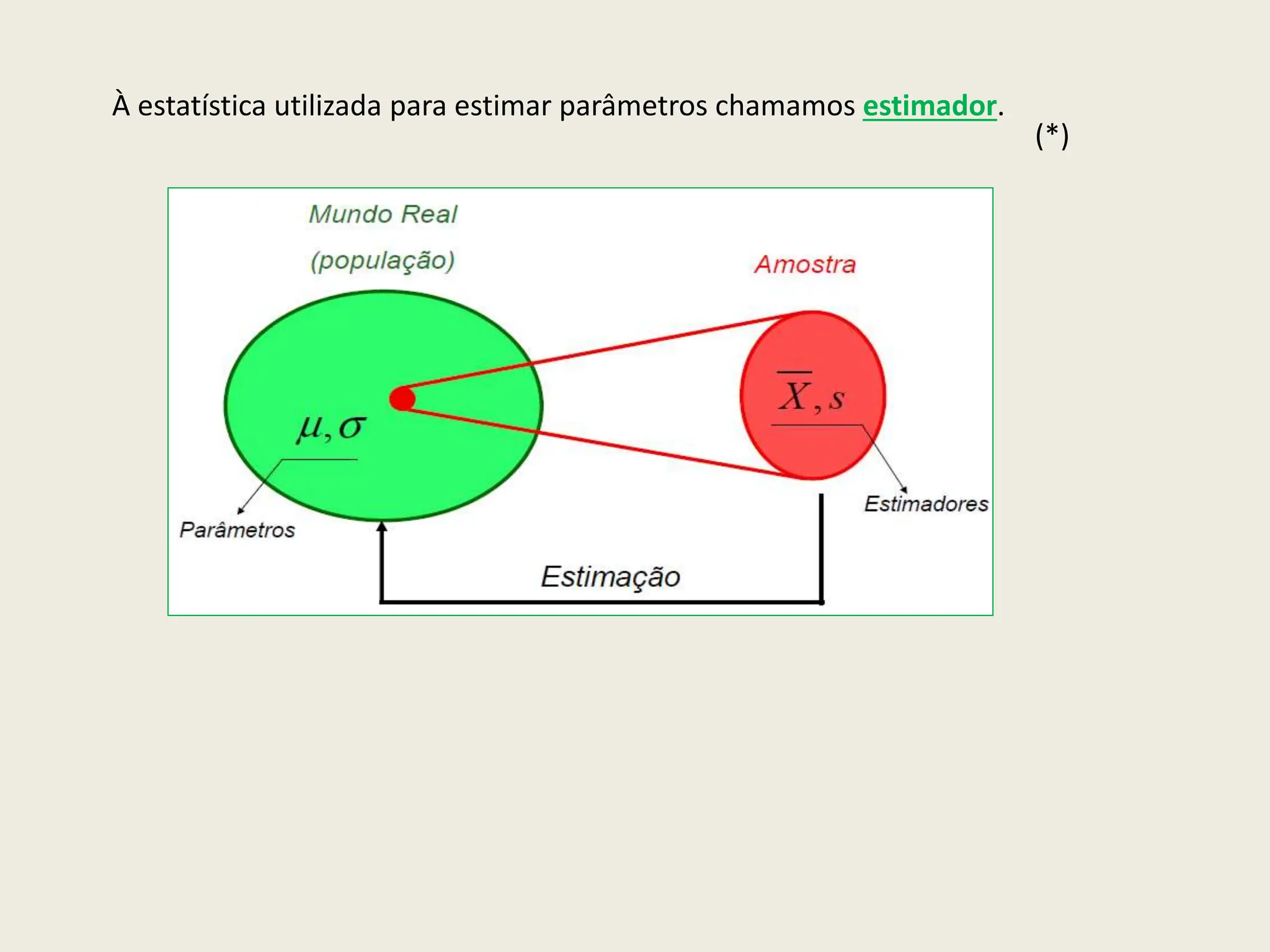
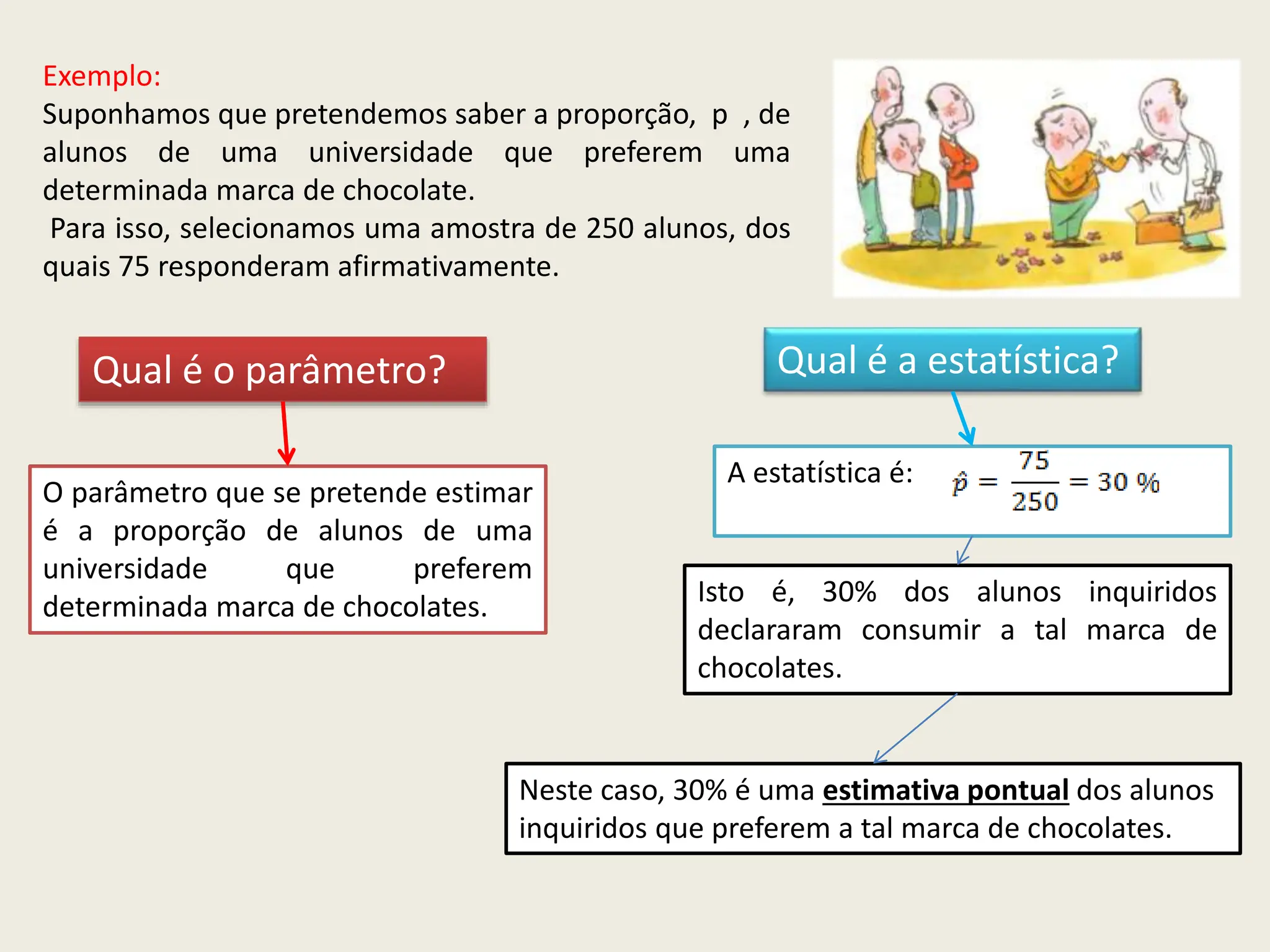
O documento apresenta uma introdução à inferência estatística, explicando conceitos essenciais como amostras, margens de erro e confiança. Discute a importância de selecionar amostras representativas para tirar conclusões sobre populações, além de descrever diferentes métodos de amostragem. Também aborda a necessidade de estimar parâmetros populacionais a partir de estatísticas obtidas de amostras.

1. Com este capítulo, pretende-se fazer uma pequena introdução à Inferência
Estatística. Serão abordados os conceitos necessários para se chegar de uma
forma simples, à interpretação e compreensão de certo tipo de informação
veiculada pela comunicação social, nomeadamente a que diz respeito às
sondagens.

2. Quando a comunicação social, a propósito de uma sondagem, transmite a
seguinte notícia :

3. Estaremos aptos a saber
interpretar o resultado de
uma sondagem?
Como interpretamos a ficha técnica que a acompanha?
Com este capítulo pretendemos
responder a esta questão.
Porquê uma amostra de 1964
indivíduos ?
O que é a margem de erro?
O que se entende por confiança?

4. Ciência que estuda a variabilidade apresentada
pelos dados.
Tal como refere David Moore, podemos considerar três grandes áreas nesta ciência
dos dados:
Aquisição de dados
O tema da Aquisição de dados, merece relevo especial, pois deverão ser
recolhidos numa perspetiva em que será a partir da informação que eles
fornecem que iremos responder a determinadas questões, isto é, retirar
conclusões para as Populações subjacentes a esses dados – contexto em que tem
sentido fazer Inferência Estatística.
Permite-nos, a partir dos dados retirar conclusões, mas também exprimir o
grau de confiança que devemos ter nessas conclusões.
É precisamente nesta particularidade, que se manifesta toda a
potencialidade da Estatística.
O que é a Estatística?
Inferência a partir dos
dados
Análise de dados

5. Estatística
onde se procede à
organização e
interpretação de dados;
( estudada no 10º ano)
onde se estuda a
possibilidade de
quantificar
acontecimentos ou
situações influenciadas
por fatores aleatórios;
( estudada no 2º período)
onde se procede à análise e
interpretação de amostras
com o objetivo de inferir
conclusões acerca da
população (de onde se
extrai a amostra);
( a estudar neste capítulo).
Estatística
Descritiva
Teoria da
Probabilidade
Inferência
Estatística

6. Inferência Estatística
É um processo de
raciocínio indutivo, em
que se procuram tirar
conclusões indo do
particular, para o geral.
Utiliza-se quando se
pretende estudar
uma população,
estudando só alguns
elementos dessa
população, ou seja,
uma amostra.
Serve para, a partir das
propriedades
verificadas na amostra,
inferir propriedades
para a população.
O que é ? Quando se
utiliza ?
Para que
serve ?
utilizam-se amostras para, depois de estudadas, tirar conclusões sobre as populações
de onde foram extraídas.
(*)

7. População é o conjunto de todos os elementos de um
estudo, com uma ou mais características comuns.
Amostra é um subconjunto finito com elementos de
uma população
(*)

8. Mas por que razão utilizamos amostras, cujas conclusões podem ser erróneas, e não
estudamos todos os elementos de uma população, o que permite atingir conclusões
muito mais fiáveis?
Há muitas situações em que, simplesmente, não é viável a utilização da totalidade da
população
Exemplo 1: Impossibilidade de reutilização dos
elementos da população analisados
Para testar a qualidade da produção diária
(população) numa fábrica de bolachas seria impraticável
prová-las todas, pois deixaria de haver artigo para
comercializar.
Exemplo 2: Custos muito elevados para analisar todos os
elementos da população
Consideremos uma unidade fabril que produz
componentes eletrónicos e circuitos integrados. Seria
praticamente impossível testar todos os componentes e
circuitos, não só em termos de custos (muito dispendioso)
como em termos de tempo.

9. AMOSTRA
Amostragem
Simples
Amostragem
sistemática
Amostragem
estratificada ou
proporcional
Existem vários métodos para selecionar uma amostra:
Amostragem por
grupos (clusters)

10. todos os elementos selecionados têm a mesma probabilidade de fazer parte da
amostra. Um processo muito comum na obtenção deste tipo de amostra é a
utilização de números aleatórios (gerados por computador)
Exemplo: Para um determinado estudo, uma empresa precisa de uma amostra de
dimensão 25, a extrair dos seus 2500 funcionários.
Para conseguir uma amostra aleatória simples basta atribuir a cada um dos
funcionários da empresa um número entre 0001 e 2500. Em seguida, com o auxílio
de um computador, gera-se uma sucessão de 25 desses números e selecionam-se
os funcionários a que correspondem os números extraídos ( ou colocar os números
num saco e extrair 25)
AMOSTRAGEM SIMPLES
Menu 1 –optn-prob-rand-Int-
RandInt#(1,25,5)

11. os elementos da população são selecionados através de um processo definido a
priori.
Exemplo: Consideremos a mesma empresa do exemplo anterior e os mesmos 2500
funcionários, dos quais continuamos a querer uma amostra de 25 elementos.
Se atribuirmos um número 0001 a 2500, a cada um dos funcionários e escolhermos
um elemento de 100 em 100, no final teremos uma amostra de 25 elementos
selecionados de forma sistemática.
AMOSTRAGEM SISTEMÁTICA

12. os elementos da população são pré-selecionados segundo o estrato a que
pertencem (social, cultural, etário, sexual,etc.). Em seguida, recolhem-se amostras
aleatórias simples de cada estratos (proporcional à representatividade do estrato),
que se juntam numa amostra única que é, sem dúvida, mais representativa da
população.
Exemplo: Suponhamos que vamos realizar um estudo acerca de uma vasta região
arbórea e precisamos de uma amostra.
Podemos dividir a população de árvores segundo a espécie e, a partir daí, escolher
uma amostra (proporcional) de cada espécie. Em seguida, juntamos as amostras de
cada espécie numa única amostra representativa da população de árvores e, com
esta, procedemos ao estudo visado.
AMOSTRAGEM ESTRATIFICADA OU PROPORCIONAL

13. a população é dividida em grupos, onde cada grupo é representativo da população.
Seleciona-se aleatoriamente um conjunto de grupos e a amostra é constituída por
todos os elementos dos grupos selecionados.
Exemplo: pretende-se estudar as habilitações dos pais dos alunos de uma escola.
Seleciona-se uma turma de cada ano de escolaridade que vai representar a
amostra.
AMOSTRAGEM POR GRUPOS (CLUSTERS)

14. Qualquer que seja o método de amostragem escolhido, para que a amostra seja
representativa da população é indispensável que:
• Qualquer elemento da amostra tenha a mesma probabilidade de nela
figurar;
• Tenha um número de elementos que permita, com algum rigor, inferir
para a população as conclusões a que chegamos;
• Estejam representadas, de forma proporcional, as características da
população, quer qualitativas quer quantitativas.
Mesmo respeitando os métodos de amostragem, a generalização dos resultados à
população (inferência) tem sempre algum erro associado !!

15. Parâmetro e Estatística. Estimativa pontual
AMOSTRA obtenção de informações
acerca da população de onde ela foi
extraída
Objetivo
PARÂMETROS (que
descrevem a população)
Exemplo: Nas duas escolas secundárias de “Rio Bravo”, realizou-se um estudo que visava
determinar o valor médio, μ , das idades dos alunos do 11º ano.
Para isso recolheu-se uma amostra aleatória de 70 alunos (dos 350 que frequentam o
11º ano nas duas escolas), tendo-se obtido um valor para a média amostral,
À média amostral, , chamamos estatística
Ao valor médio, μ, chamamos parâmetro.
(*)

16. PARÂMETROS Valor que caracteriza uma população
ESTATÍSTICA Valor que caracteriza a amostra
Uma estatística serve para estimar parâmetros, isto é, se quisermos estimar valores
desconhecidos de uma população, podemos utilizar estatísticas adequadas ao
parâmetro em questão.
utilizar as estatísticas adequadas para poder inferir
sobre os valores dos parâmetros.
Estimar parâmetros
(*)

17. Parâmetro Estatística
Valor médio - μ Média amostral -
Proporção populacional (frequência
relativa) de determinada característica - p
Proporção amostral (frequência relativa)
da característica em questão -
Variância populacional – Variância amostral -
Desvio padrão populacional - σ Desvio padrão amostral - s
(*)

18. À estatística utilizada para estimar parâmetros chamamos estimador.
(*)

19. Exemplo:
Suponhamos que pretendemos saber a proporção, p , de
alunos de uma universidade que preferem uma
determinada marca de chocolate.
Para isso, selecionamos uma amostra de 250 alunos, dos
quais 75 responderam afirmativamente.
O parâmetro que se pretende estimar
é a proporção de alunos de uma
universidade que preferem
determinada marca de chocolates.
Qual é o parâmetro? Qual é a estatística?
A estatística é:
Isto é, 30% dos alunos inquiridos
declararam consumir a tal marca de
chocolates.
Neste caso, 30% é uma estimativa pontual dos alunos
inquiridos que preferem a tal marca de chocolates.

20. ESTIMATIVA PONTUAL DE UM
PARÂMETRO ϴ
valor numérico (único) assumido
pela estatística ,


Por exemplo, podemos considerar que é uma estimativa pontual do
parâmetro μ .
X
( Ficha de trabalho - exercícios: 1,2,3,4)
(*)